7. Блочні задачі лінійного програмування та підходи до їх розв’язування

Для більшості практичних задач ЛП характерною є їх велика розмірність (наявність багатьох змінних та обмежень) і розрідженість (наявність великої кількості нульових елементів) в матриці обмежень. Класичні методи в цьому випадку виявляються малопридатними, що привело до розроблення як точних, так і наближених методів для розв’язування задач великої розмірності такого типу. В основному ці методи використовують прийом декомпозиції, тобто розбиття первісної задачі великої розмірності на ряд підзадач меншої розмірності, які незалежно розв’язуються за допомогою класичних методів, та координації, або узгодження незалежних розв’язків, виходячи з наявності спільних обмежень. Цей процес ітеративно повторюється до моменту отримання оптимального розв’язку задачі загалом, або ж до того моменту, коли будуть виконані умови зупинки.

Методи розв’язування задач великої розмірності ґрунтуються також на вивченні структури матриці обмежень і застосовуються в більшості до матриць блочно-діаґональної структури, один з підвидів яких виглядає наступним чином:

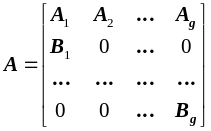, де - підматриці. Змістовно задачу такого типу можна розглядати наступним чином. До складу фірми, що випускає певні вироби, входить відділень, кожне з яких для виробництва використовує незалежні від інших відділень автономні ресурси (для -го відділення норми витрат незалежних ресурсів відображаються підматрицею . Окрім того, в розпорядженні керівництва фірми є спільні ресурси, норми витрат яких задані зв’язуючим рядком матриці обмежень. Необхідно побудувати такий план виробництва, для якого б досягався максимальний прибуток фірми загалом.

Відповідна задача ЛП формулюється наступним чином:

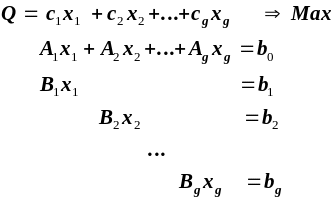
Вважаючи, що множини , , — непусті та обмежені (ця умова не є обмежуючою), а , — екстремальні точки цієї множини, будь-яка з точок множини може бути представленою у вигляді опуклої комбінації крайніх точок, тобто , . Підставивши отримані співвідношення в умову первісної задачі, отримаємо:

...

Ця задача є головною — координуючою задачею, в якій невідомі значення (припускаючи, що відомі значення координат всіх крайніх точок кожної з множин ). Якщо ми знайдемо ці значення, то цим самим розв’яжемо задачу.

Оптимальний розв’язок знаходиться за допомогою дворівневої процедури, яка має назву методу Данціґа-Вулфа. В координуючій задачі кількість обмежень становить , що суттєво менше, ніж кількість обмежень , де , - кількості рядків у матрицях відповідно. Але кількість стовпчиків у координуючій задачі надзвичайно велика - рівна числу всіх крайніх точок множин . Якщо б розв’язувати цю задачу безпосередньо, то ніякого виграшу в порівнянні з первісною задачею не було б. У методі Данціґа-Вулфа не зберігаються всі стовпці матриці обмежень координуючої задачі — вони отримуються по мірі необхідності з використанням методу ґенерації стовпців та розв’язуванням множини допоміжних підзадач з використанням первісних підматриць .

Представимо координуючу задачу в еквівалентній формі:

, ,..., , ,

де , .

Розв’язання цієї задачі відносно невідомих дозволяє знайти остаточний розв’язок, тому що . При розв’язуванні головної задачі за допомогою модифікованого симплекс-методу потрібно ідентифікувати змінні, що вводяться та виводяться з бази. На перший погляд може здатися, що для цього потрібно знання всіх кутових точок . Однак сенс побудови головної задачі при використанні методу декомпозиції полягає в тому, що цю задачу можна розв’язати, маючи лише одну екстремальну точку, що відповідає змінній, яка вводиться до бази. Після знаходження цієї точки можна чисельно визначити всі елементи вектора, що включається до бази, а також відповідне значення . Після цього вектор, що виключається з бази, знаходиться звичайним шляхом у відповідності до умов припустимості симплекс-методу.

Таким чином укрупнена схема алгоритму декомпозиції включає два етапи:

• перетворення первісної задачі в координуючу шляхом непрямого представлення простору розв’язків кожної підзадачі у вигляді опуклої комбінації його екстремальних точок;

• формування вектора-стовпчика, що асоційований зі, змінною, яка включається до бази, та використання отриманого результату для визначення вектору, що виключається з бази.

Останній етап алгоритму реалізується за допомогою процедури ґенерації стовпчиків, за допомогою якої й отримують значення компонент, що включаються до бази.

Розглянемо деталі реалізації цієї процедури. Нехай — біжуча база, а — вектор коефіцієнтів функції мети при базових змінних. Згідно до схеми обчислень модифікованого симплекс-методу біжучий розв’язок є оптимальним, якщо для всіх небазових векторів виконується умова оптимальності , де згідно до визначення координуючої задачі та 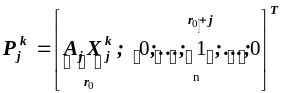, одиничний вектор має компонент, одиниця знаходиться в -ій позиції. Здійснимо наступні перетворення. Нехай , де — матриця , що складається з перших стовпчиків матриці , а — -й стовпчик цієї ж матриці. У цьому випадку

= .

Якщо біжучий розв’язок неоптимальний, то вектор , для якого значення від’ємне і найбільше за абсолютним значенням повинен бути включений до бази. У цьому випадку суттєвим є те, що не можна обчислити до тих пір, поки не відомі всі елементи , що в свою чергу є неможливим, поки не відома відповідна кутова точка . Найсуттєвіша складова алгоритму власне й пов’язана з розв’язанням цієї проблеми.

Замість того, щоб знаходити всі кутові точки всіх n підмножин, задачу можна звести до визначення кутової точки кожної з підмножин, якій відповідатиме найменше значення .

Нехай та . Таким чином, якщо , змінна , що відповідає , повинна бути введена до бази. В іншому випадку, якщо , отриманий розв’язок є оптимальним. Кожна з екстремальних кутових точок визначається внаслідок розв’язання наступної задачі ЛП:

.

В цій задачі індекс k не вживається з наступної причини. Внаслідок припущення про обмеженість множини мінімальне значення також обмежене і повинно відповідати деякій кутовій точці цієї множини. Оскільки = і — постійна, що не залежить від k, задача переформульовується наступним чином:

Звідси визначаємо , де — оптимальне значення . Змінна, що виводиться з бази, знаходиться згідно до умови припустимості, що використовується в модифікованому симплекс-методі.

Таким чином алгоритм декомпозиції складається з наступних кроків:

1. Перетворити первісну задачу таким чином, щоб в її модифікованому формулюванні фіґурували нові змінні .

2. Знаходимо початковий базовий розв’язок модифікованої задачі. (На цьому кроці доцільно застосувати перший етап двоетапного симплекс-методу.

3. На біжучій ітерації знайти для кожної з підзадач та визначити . Якщо , то знайдений розв’язок оптимальний — стоп.

4. Включити змінну , що відповідає , до бази. Визначити змінну, що виключається з бази, виключити її та обчислити нову матрицю . Перейти до кроку 3.