5. Основные формулы структурной кристаллографии

Межплоскостные расстояния для серии плоскостей (hkl) определяют по формуле

. (5.1)

Длина вектора вычисляется по формуле

(5.2)

Однако столь громоздкой формулой приходится пользоваться лишь для триклинных кристаллов, а для остальных в силу соответствующих соотношений между параметрами решётки формулы существенно упрощаются:

для моноклинной сингонии

, (5.2а)

где ; ; ; ;

для ромбической сингонии

(5.2б)

где ;

для гексагональной сингонии

, (5.2в)

где ;

для тригональной сингонии

, (5.2г)

где ;

для тетрагональной сингонии

, (5.2д)

;

для кубической решётки

, (5.2е)

где

Формула (5.2е) особенно наглядно показывает, что межплоскостное расстояние, а значит, и ретикулярная плотность плоскостей уменьшаются по мере увеличения индексов плоскостей.

Заметим, что значения d_hkl , получаемые из уравнения 5.1, - это отсчитываемые по нормали расстояния между любыми пареллельными плоскостями, отсекающими на осях координат отрезки a/h, b/k, c/l; эти плоскости не обязательно являются атомными сетками. Если h, k, l – целые числа, не имеющие общего множителя, то они представляют собой миллеровские индексы плоской атомной сетки. По формулам (5.1) и (5.2) вычисляются межплоскостные расстояния семейства параллельных плоских сеток с индексами (hkl) лишь для примитивной решётки Бравэ, так как предполагается, что a, b, c определяют элементарную ячейку, содержащую один единственный узел. Если элементарная ячейка центрирована по объёму, то формула (5.1) даёт удвоенное межплоскостное расстояние для всех случаев, когда (h+k+l) нечётное. Например, расстояние между плоскостями (100) в объёмно-центрированной решётке, очевидно, равно лишь половине величины d_hkl , определяемой по формуле (5.1). Чтобы получить истинное межплоскостное расстояние, надо удвоить миллеровские индексы в объёмно-центрированной решётке, если сумма (h+k+l) – нечётная, в гранецентрированной, если h, или k, или l – нечётное (нуль считают чётным числом), и в базоцентрированной, например С-решётке [центрирована плоскость(001)], если (h+k) – нечётное.

Объём элементарной ячейки вычисляется по формуле:

. (5.3)

Раскрывая скобки по правилам векторного исчисления, получим

, (5.4)

т.е. . (5.4а)

Так вычисляется объём триклинной примитивной ячейки, а для остальных сингоний формула (5.4) упрощается.

Объём элементарной ячейки равен:

в моноклинной сингонии

; (5.4б)

в ромбической сингонии

; (5.4в)

в гексагональной сингонии

; (5.4г)

в тригональной сингонии

; (5.4д)

в тетрагональной сингонии

; (5.4е)

в кубической сингонии

. (5.4ж)

Угол  между двумя плоскостями (h₁k₁l₁) и (h₂k₂l₂) находим как угол между их обратными векторами:

Записав скалярное произведение этих векторов:

, (5.5)

находим

, (5.6)

где ‑ соответствующие межплоскостные расстояния, определяемые по формулам (5.1) или (5.2). Формула (5.6) существенно упрощается по мере повышения симметрии. Итак косинус угла  между плоскостями (h₁k₁l₁) и (h₂k₂l₂) равен:

в моноклинной сингонии

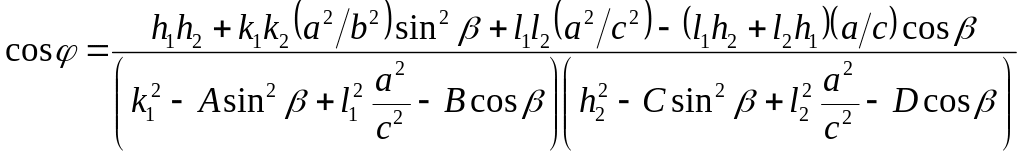, (5.7)

где ;

в ромбической сингонии

; (5.8)

в гексагональной сингонии

; (5.9)

в тригональной сингонии

, (5.9)

где ,

, ;

в тетрагональной сингонии

; (5.10)

в кубической сингонии

. (5.11)

Угол  между направлениями [u₁v₁w₁] и [u₂v₂w₂] в кристалле, т.е. между рёбрами кристалла, вычисляется как угол между векторами:

,

Составляя скалярное произведение и вычисляя его, находим

. (5.12)

Угол  между прямой и плоскостью (hkl) вычисляется с помощью обратного вектора этой плоскости по формуле

. (5.13)

Плоскость (hkl) принадлежит зоне <rst>, если вектор нормален к <rst>, т.е.

(5.13)

Получаем

.

Плоскости (h₁k₁l₁), (h₂k₂l₂) и (h₃k₃l₃) принадлежат одной зоне, если соответствующие им обратные векторы компланарны, т.е. построенный на них параллелепипед должен иметь нулевой объём:

, (5.14)

или, иначе говоря,

. (5.15)