Эквивалентность автоматов.

Определение:

Два состояния a_i и a _j называются эквивалентными, и обозначаются как a_i~a_j, если l(a_i,z_k)=l(a_j,z_k) для любого слова , то есть реакция автомата в этих состояниях на любые слова одинакова.

Определение:

Два автомата S=<Z,W,A,l,d> и S'=<Z,W,A',l',d'> называются эквивалентными, то есть S~S', если для любого a_i из A существует a_j из A' такое, что a_i~a_j, и если для любого a_j из A' существует a_i из A такое, что a_j~a_i.

Oпределение: Состояния называются k-эквивалентными, если реакция этих состояниях на слова длины k одинакова.

Отношение эквивалентности состояний есть отношение бинарной эквивалентности:

 a_i~a_j  a_i~ a_j,

  a_i~a_k & a_j~a_k  a_i~a_j.

Автоматы Мили и Мура.

    На практике наибольшее распространение получили два класса автоматов - автоматы Мили и Мура. Закон функционирования автомата Мили задается уравнениями:

a(t+1)=d(a(t),z(t));  w(t)=l(a(t),z(t)), t=0,1,2...

    Автоматами Мура называют автоматы, у которых выход зависит только от состояния, и не зависит от значения входа:

a(t+1)=d(a(t),z(t)); w(t)=l(a(t)), t=0,1,2...

    Введем понятие слова в любом из алфавитов как последовательность символов данного алфавита. Если предположить, что на входе автомата в состоянии а_i задано некоторое слово Z=z1z2z3, то по функциям l и d можно определить слово состояний и слово выходов, соответствующих этим входному слову и состоянию. Последнюю букву выходного слова при этом называют реакцией автомата в состоянии а_i на слово Z.

Эквивалентность автоматов Мили и Мура

Введены две модели автоматов:                                                                                                                        

  автомат Мура    

 автомат Мили 

        Нижеследующая теорема показывает, что эти 2 модели равномощны, т.е. любой автомат можно реализовать в каждой из этих моделей.

 

Теорема

  Для любого автомата Мура существует эквивалентный автомат Мили и наоборот.

   Доказательство теоремы построим на преобразовании автомата обного типа в автомпт другого типа, на примере конкретных автоматов, описанных с помощью графов.

Необходимость:  Докажем, что для любого(полностью определенного) автомата Мура существует эквивалентный ему автомат Мили.

                    Рассмотрим автомат Мура:

                    Sµ=<X,Y,A,  a§A>, где

               А={a1,a2,a3,a4};

X={x1,x2,x3};

Y={y1,y2};

описанный в виде графа

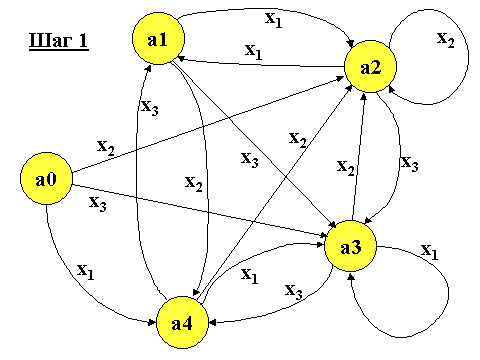
Перенесем выходы автомата с вершин графа на входящие ветви графа.

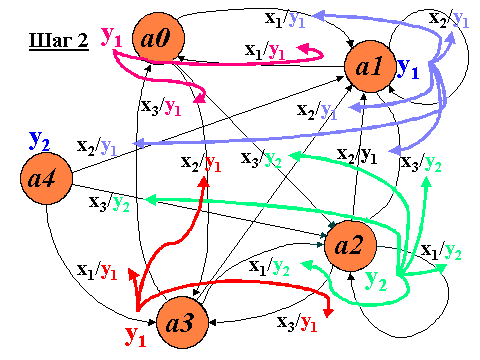
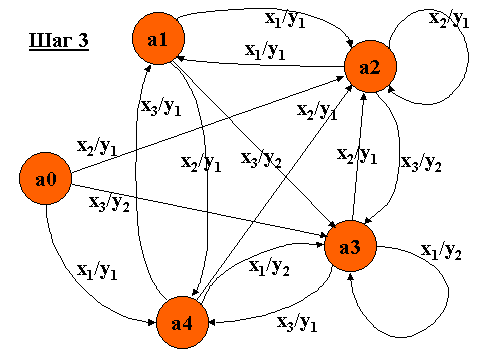
Получаем граф, который описывает автомат

                S'=<X',Y',A','a§A'>, где

                A'=А={a0,a1,a2,a3,a4};

X'=X={x1,x2,x3};

Y'=Y={y1,y2};

       Автомат S'  эквивалентен автомату S, т.к для любого состояния a1§ A aавтомата S существует состояние    a1§ A' автомата S' такое, что реакции автоматов на любые слова в этих состояниях одинаковы, и наоборот.

Достаточность:

Докажем, что для любого полностью определенного автомата Мили существует эквивалентный ему автомат Мура.

Рассмотрим автомат Мили

                S=<X,Y,A,a0§A'>, где

              А={a0,a1,a2,a3};

X={x1,x2};

Y={y1,y2,y3};

описанный в виде графа

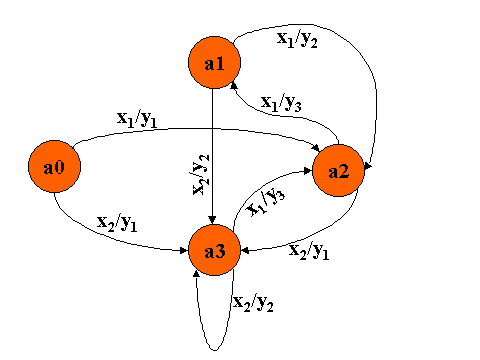
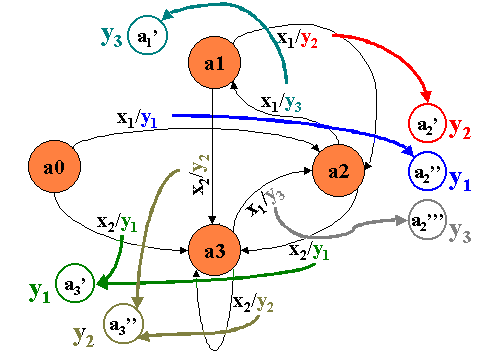
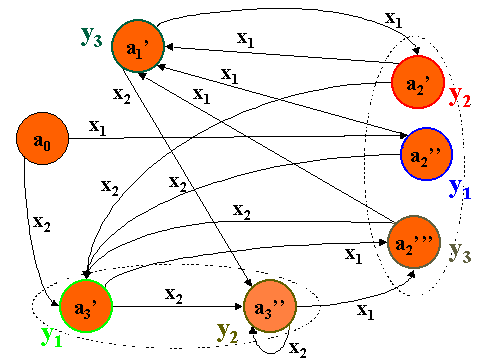
Таким образом получим граф, который описывает автомат

           S=<X',Y',A',a0§A'>, где

            A'=А={a0,a1',a2',a2'',a2''',a3',a3''};

    X'=X={x1,x2};

    Y'=Y={y1,y2,y3};

Докажем, что автоматы S и S' эквивалентны. Для этого докажем, что для любого состояния ai§A автомата S существует эквивалентное ему состояние ai§A' автомата S' и наоборот.

Покажем, что для любого состояния множества {a0,a1,a2,a3} существует эквивалентное из множества  {a0,a1',a2',a2'',a2''',a3',a3''};

        a0~a0'       

        a1~a'1

        a2~a'2

        a3~a'3

покажем обратное утверждение

a0~a0          a'1~a1        a'2~a2        a'3~a3           

                                                 a''2~a2        a''3~a3

                                               a'''2~a2