37

Федеральное агентство по образованию

Государственное образовательное учреждение высшего

профессионального образования

Тульский государственный университет

Кафедра электронных вычислительных машин

Системы управления промышленным электрооборудованием

Методические указания

по выполнению лабораторных работ

для студентов очной формы обучения

по направлению 140600 «Электротехника, электромеханика и электротехнологии»

специальности 140610

«Электрооборудование и электрохозяйства предприятий, организаций и учреждений»

Электронная версия

Тула 2008

Разработал: к.т.н., доц. Ю.И. Лебеденко

Рассмотрено

на заседании кафедры

Протокол №

от «____» 2008 г.

Зав. кафедрой ЭВМ

В.С. Карпов

«____» 2008 г.

Нормоконтролер

Ответственный за

стандартизацию на кафедре

________________

В.Л. Токарев

«____» 2008 г.

Данные методические указания предназначены для студентов специальности 140610 «Электрооборудование и электрохозяйства предприятий, организаций и учреждений», изучающих основы системы управления в качестве общепрофессиональной дисциплины в пятом и шестом учебном семестрах. Предполагается, что студенты обладают необходимыми знаниями по высшей математике, физике, электротехнике и основам электроники.

Поскольку основным методом исследования систем управления является их моделирование, то для выполнения лабораторных работ предполагается применять современные средства в виде персонального компьютера, оснащенного исследовательским программным пакетом MatLab (v.6.0 и выше). В ходе выполнения работы студенты уточняют основные теоретические положения, а затем решают практическую задачу, поставленную преподавателем. Рекомендуется использовать в качестве исходных данных для лабораторных работ данные, которые являются вариантом задания по курсовому проекту, выполняемому в рамках данной дисциплине.

После выполнения работы студент оформляет отчет, в котором указываются название работы, ее цель и основные задачи, отображается порядок выполнения работы, подтверждаемый реальными вычислениями, результаты выполнения, иллюстрируемые полученными формулами, таблицами и графиками.

Содержание

Лабораторная работа 1

Исследование математических моделей электротехнических объектов управления …4

Лабораторная работа 2

Получение передаточных функций разомкнутых и замкнутых систем. Преобразование структурных схем систем автоматического управления …………………………………………10

Лабораторная работа 3

Построение частотных характеристик систем автоматического управления ……….20

Лабораторная работа 4

Оценка устойчивости линейных автоматических систем …………………………….25

Лабораторная работа 5

Исследование точности работы автоматических систем ………………………………29

Лабораторная работа 6

Синтез корректирующих устройств в линейных системах ……………………………34

Библиографический список ………………………………………………………………………………………. 38

Лабораторная работа1

Исследование математических моделей электротехнических объектов управления

1. Цель работы

Ознакомиться с порядком и правилами составления дифференциальных уравнений автоматической системы, с функциями и командами системы MatLab. Получить навыки численного решения дифференциальных уравнений в программной системе MatLab.

2. Теоретические положения

При составлении дифференциальных уравнений систем автоматического управления всегда используются физические законы, описывающие конкретное техническое устройство, механизм, прибор. Порядок составления дифференциальных уравнений системы лучше всего рассмотреть на примере.

Рассмотрим следящий электромеханический привод (рис.1.1):

В этой системе _- входной угол; _ - выходной угол поворота объекта управления. Их разность (_ -_)служит сигналом управления для двигателя.

Для каждого отдельного узла сервопривода можно написать дифференциальное или алгебраическое уравнение:

1. Чувствительный элемент:

Выходное напряжение потенциометра P₁ определиться как

U₁=k₁₁.

На выходе P₂ имеем:

U₂=k₁₂,

где k₁-коэффициент передачи потенциометра. Следовательно

U=U₁-U₂=k₁(₁-₂)=k₁.

2. Усилители. Если рассматривать их как безынерционные элементы с помощью коэффициентами передачи k₂ и k₃, то с учетом того, что на входе второго усилителя выход первого суммируется с сигналом обратной связи тахогенератора, получим:

U_e=(k₂U-U_tg)k₃

3. Обмотка возбуждения генератора. Дифференциальное уравнение можно записать на основе закона Кирхгофа:

где L_e и r_e –величины индуктивности и активного сопротивления обмотки.

4. Генератор. Для генератора с линейной характеристикой ЭДС может быть вычислена по формуле:

e=k₅i_e; ;

5. Электродвигатель имеет две степени свободы. Соответственно, его описание будет иметь два дифференциальных уравнения первого порядка:

- для электрической части

- для механической части.

где L_r и r_r – индуктивность и активное сопротивление обмотки ротора,

С’_E и С’_М - коэффициенты пропорциональности,

J – момент инерции, приведенный к оси двигателя,

 - угловая скорость ротора,

M – момент нагрузки.

Если считать магнитный поток возбуждения двигателя постоянным, =const, то

где U_nom, M_nom, I_{r nom} – номинальные значения напряжения ан двигателе, вращающего момента и тока якоря;

₀ – угловая скорость ротора без нагрузки.

Угол вращения двигателя связан со скоростью через простое соотношение

.

6. Редуктор. Если характеристика механизма линейная, то ее можно описать алгебраическим выражением:

где q – коэффициент передачи редуктора.

7. Тахогенератор. Выходное напряжение этого устройства пропорционально скорости вращения двигателя:

Объединим все уравнения компонентов в единую систему

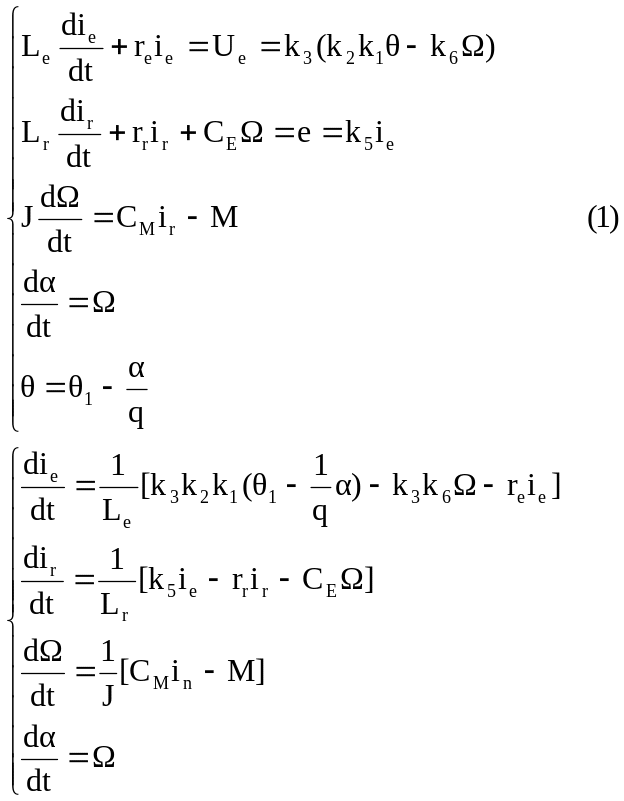
В этой системе в качестве входного воздействия выступает θ₁[rad], как возмущающее воздействие . В ней можно выделить четыре независимых переменных: θ₂[rad] – выход; Ω [rad/s]; i_r[A] и i_e[A].

Выведенные уравнения можно привести к относительным единицам. Для этого примем в качестве основной одну из фазовых переменных (чаще всего это выходная величина), измеряемую в конкретных физических единицах.

После этого можно пересчитать все коэффициенты в уравнениях так, чтобы они выражались в безразмерных единицах:

Пусть i_e = x₁; i_r = x₂; Ω = x₃; α = x₄; θ₁ = y₁; M = y₂.

Тогда

Легко видеть, что многие K_ij равны нулю в системе (2).

будем называть фазовыми координатами.

Для данной системы можно записать одно дифференциальное уравнение четвертого порядка

,

В общем виде:

(a₄p⁴+a₃p³+a₂p²+a₁p+a₀)x=y₁b₁+y₂b₂ (3),

или в еще более отвлеченной форме:

D(p)x(t)=Q(p)g(t)+N(p)f(p).

Это уравнение дает сокращенную форму записи дифференциальных уравнений системы через передаточные функции.

Для решения дифференциальных уравнений систем автоматического управления можно использовать систему MatLab.

Основное окно системы MatLab называется командным окном, в котором имеется традиционное для Windows-приложений меню и клиентская часть с символом приглашения >>. Также имеется полоса прокрутки окна.

После приглашения с клавиатуры можно вводить числа, имена переменных, знаки операций, которые составляют выражение. Имена переменных должны начинаться с буквы, могу включать цифры и символы подчеркивания.

После выполнения команды информация из зоны редактирования переходит в верхнюю часть окна, являющуюся зоной просмотра. Оттуда с помощью буфера обмена информация может быть помещена в зону редактирования или в другие приложения. Зона редактирования может быть расширена до двух и более строк после символа >> путем набора трех и более точек., однако в предыдущих строках уже при этом нельзя ничего менять. Команда clc позволяет очистить видимое пространство командного окна, но это не затронет памяти командного окна.

Кроме основного вся информация о ранее произведенных действиях может быть отражена также с помощью окон Command History и WorkSpace. Обратившись к ним с помощью мыши можно повторить ввод переменной или выражения в зону редактирования.

Неиспользуемые переменные можно очистить из памяти командного окна, используя команду clear, а просмотреть список имеющихся переменных - командой who.

Введенную информацию можно сохранять и загружать из файлов системы, имеющих расширение .mat.

Особо важную роль в записи выражений играет точка с запятой. Во-первых, ставя её в конце выражения, можно не выводить результат на экран, что используется при промежуточных вычислениях. Во-вторых, точка с запятой работает как разделитель, когда несколько введенных выражений будут вычисляться одним нажатием клавиши Enter.

В системе MatLab присутствуют все основные элементарные функции:

^ -возведение в степень; sqrt – извлечение квадратного корня; exp – возведение в степень числа е; pow2 – степень числа 2. Также присутствуют обратные к ним функции: log – натуральный логарифм; - log10 - десятичный логарифм; log2 - по основанию 2. Тригонометрические функции также представлены весьма полно: sin, cos, tan, cot и обратные к ним: asin, acos, atan, acot.

Для решения систем дифференциальных уравнений в MatLab имеются «интеллектуальные решатели». Это функции ode23, ode45, ode113, ode15s, ode23s, ode23t, ode23tb. Функции с суффиксом s предназначены для решения так называемых систем жестких дифференциальных уравнений, а для остальных наиболее употребительной является функция ode45, реализующая алгоритм Рунгe-Кутта 4-5 порядков (разные порядки используются в нем для контроля шага интегрирования).

Для применения функции необходимо записать дифференциальные уравнения в нормальной форме Коши:

y1’=F1(t, y1, y2, …, yn);

y2’=F2(t, y1, y2, …, yn);

……………………….

yn’=Fn(t, y1, y2, …, yn);

Введем вектор-столбцы Y и F, состоящие из y1, y2, …yn и F1, F2, …Fn соответственно. Тогда в векторной форме система дифференциальных уравнений примет вид:

Y’=F(t, Y);

Чтобы применить решатель ode45 надо оформить в виде собственной M-функции правую часть системы уравнений.

Пусть, например, необходимо решить систему дифференциальных уравнений:

y₁’=y₂+K*t²;

y₂’=-y₁;

с начальными условиями у₁(0)=0, у₂(0)=1 на интервале времени t от 0 до 12 секунд.

Неизвестная вектор-функция Y состоит из двух элементов Y=[y(1), y(2)]. Т.к. функции у(1) и у(2) вычисляются во многих точках в процессе нахождения решения, то реально у(1) и у(2) являются векторами-столбцами. Вектор правых частей F системы уравнений для К=0,01 вычисляем с помощью собственной M –функции MyDifEq1:

function dydt = MyDifEq1(t, y)

dydt= [ 0.01*t*t +y(2); -y(1) ];

текст которой записываем в файл MyDifEq1.m . Она вызывается каждый раз, когда требуется вычислить правые части в конкретной точке t, так что здесь t является скаляром, а вектор у состоит всего из двух элементов.

Для вызова решателя системы дифференциальных уравнений в командном окне указывается имя функции, соответствующей нужному методу, а в качестве трех обязательных аргументов функции используют указатель на m-файл, диапазон интегрирования по времени и вектор начальных условий по переменным состояния системы. Например, для решения описанной системы дифференциальных уравнений в командной строке записывается

>>[T,Y]=ode23(@MyDifEq,[0 12],[0;1])

Результатов вычислений здесь служит массив фазовых координат – компонент вектора Y, записанный с определенным шагом по независимой переменной интегрирования Т (по времени). Комплексные числа записывают в MatLab также традиционным образом:

2+3i; -6.78+0.64e-3*i; 4 – 2 j. Необходимая форма числа (действительное или комплексное) выбирается системой при производстве вычислений автоматически. Для работы с комплексными числами предназначены следующие функции: abs (модуль), conj (сопряженный комплекс); real, imag (действительная и мнимая части); angle (аргумент).

Решение дифференциальных уравнений хорошо визуализировать с помощью функции построения графиков plot:

plot(T,Y(:,1),'-', T,Y(:,2),'-.');

Здесь для каждой отображаемой на графике скалярной функции в кавычках указывается тип соответствующей линии.

Для функции одной вещественной переменной график строится с помощью следующих выражений, например:

x=0: 0.01: 2;

y=sin(x); - вычисляется массив функции у по аргументу х в указанных пределах с указанным шагом, после чего вызовом функции

plot(x,y)

генерируется графическое окно, в котором будет построен график.

Команда clf позволяет очистить окно, а команда cla – удаляет только график.

Если нужно построить второй график поверх первого , то перед вторым вызовом функции plot следует выполнить команду hold on. Также можно применить команду с несколькими параметрами plot(x,y,x,z), выводящую сразу несколько графиков разным цветом. Для создания нового графического окна применяют команду figure.

Для вывода нескольких разных графиков в составе одного окна применяют функцию subplot, которая принимает три числовых параметра: первый из них равен числу подобластей, второй – числу колонок подобластей, а третий – номеру подобласти.

C помощью специальных маркеров функции plot можно также задавать цвет и тип линий графиков.

Если существует необходимость отказаться от автоматического формирования масштабов изображения, можно применить функцию масштабирования

axis ( [ xmin, xmax, ymin, ymax ] ). Например, эту функцию можно применять сколько угодно раз подряд, чтобы найти графически значение корня уравнения.

В графическом окне также можно применять изменения цвета фона, выводить произвольный текст.

Чтобы построить график сложной функции, в которой используется перемножение нескольких переменных необходимо перед знаком умножения ставить точку, что служит сигналом для использования переменной как скаляра. В противном случае MatLab воспримет массивы переменных как векторы и выдаст сообщение об ошибке при перемножении массивов с несовпадающей размерностью.

3. Варианты заданий на работу

При выполнении работы необходимо промоделировать в программе MatLab следующую систему (по вариантам). Числовые параметры системы задаются преподавателем или выбираются студентом самостоятельно.

1) Электродвигатель постоянного тока

2) Асинхронный электродвигатель переменного тока

3) Электрогенератор постоянного тока

4) Асинхронный генератор переменного тока

4. Контрольные вопросы

1. Что называется динамической системой?

2. Приведите основные признаки классификации динамических систем.

3. Дайте определения объекта регулирования и регулятора.

4. Поясните принципы управления по разомкнутому и замкнутому контуру.

5. В чем различие между прямым и непрямым регулированием?

6. Перечислите основные функциональные элементы системы автоматического регулирования.

7. Как осуществляется переход от физических узлов системы к их математическому описанию?

8. Почему к системам автоматического управления часто применяется процедура линеаризации?

9. Что называется безразмерной системой уравнений?

10. Для чего служит передаточная функция системы?

Лабораторная работа 2

Получение передаточных функций разомкнутых и замкнутых систем. Преобразование структурных схем систем управления

2.1 Цель работы

Уяснить сущность передаточных функций и символику структурных схем систем автоматического управления. Ознакомиться с общими правилами преобразования структурных схем. Получить практические навыки преобразования схем и использования пакета Simulink системы MatLab.

2.2. Теоретические положения

Передаточная функция объекта управления или элементарного звена – это отношение изображений по Лапласу выходной величины объекта к изображению входной величины при нулевых начальных условиях. Динамическим звеном будем называть такую часть линейной динамической системы, которую можно описать обыкновенным дифференциальным уравнением не выше второго порядка.

Рассмотрим получение передаточных функций элементарных динамических звеньев.

С использованием теоремы об изображении производной легко прейти от описания звена в виде дифференциальных уравнений к передаточной функции.

Классификация динамических звеньев определяется типом описывающих их дифференциальных уравнений.

Пусть x₁ – входная величина звена, а x₂ – выходная. Статическая характеристика любого линейного звена будет представлять собой прямую линию.

Для позиционных звеньев эта линия выражает зависимость между входной и выходной переменными величинами.

x₂=kx₁,

где k – коэффициент передачи звена.

Для интегрирующих звеньев линейная зависимость связывает производную выходной величины с первообразным входным сигналом:

В установившемся положении

где k – коэффициент передачи [с^-1].

Для дифференцирующих звеньев получаем выражение

где коэффициент k– имеет размерность времени [с].

Рассмотрим описание основных типов динамических звеньев, их дифференциальные уравнения и временные характеристики.

1. Позиционные динамические звенья

a.1. Безынерционное звено

Это звено описывается простым алгебраическим уравнением не только в статике, но и в динамике:

x₂=kx₁.

Его передаточная функция равна константе:

W(p)=k.

Этот тип динамических звеньев используется для описания широкого класса технических устройств ( быстродействующие электронные усилители редукторы без люфта и т.п.)

Переходная характеристика (реакция на единичный скачок): h(t)=k 1(t).

Весовая функция (реакция на идеальный импульс): w(t)=k δ(t).

a.2. Апериодическое звено первого порядка

Это звено можно описать дифференциальным уравнением вида:

Передаточная функция: .

Такое описание характерно, например, для электродвигателя (с линейной механической характеристикой), R-C-цепи, газового ресивера, и т.д.

Временные характеристики звена описываются формулами:

и представлены на рис.2.1.

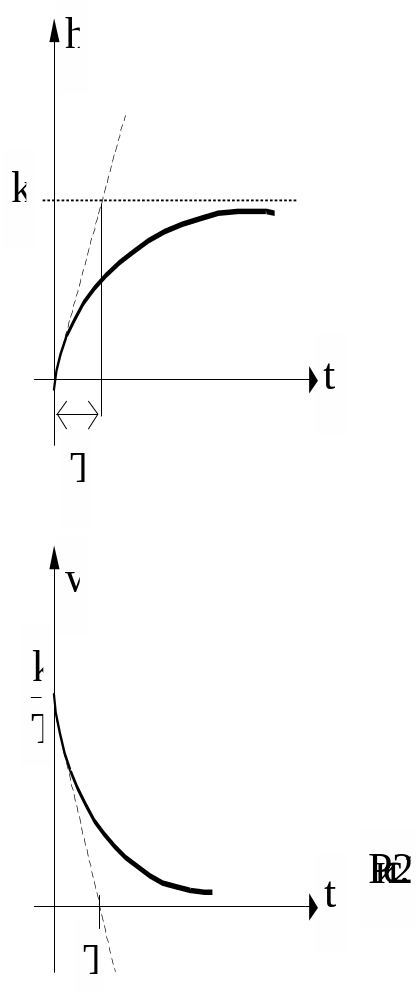
a.3. Колебательное звено

Звено имеет второй порядок. В операторной форме дифференциальное уравнение такого звена можно представить следующим образом:

где - угловая частота собственных колебаний;

0<ξ<1 – коэффициент демпфирования.

Такая математическая модель используется для описания RLC–цепи, колебательных механических систем с вязким трением и проч.

Передаточная функция колебательного звена:

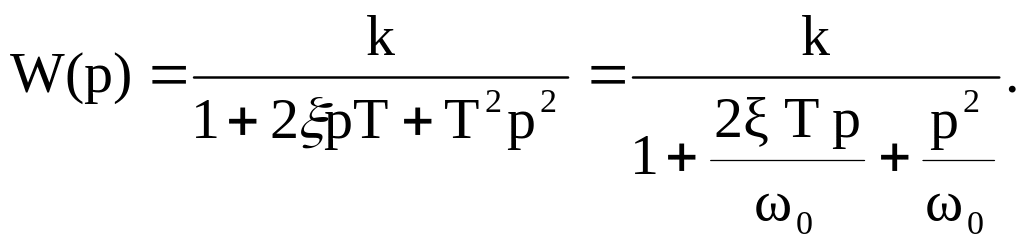
Корни характеристического уравнения колебательного звена всегда являются комплексными:

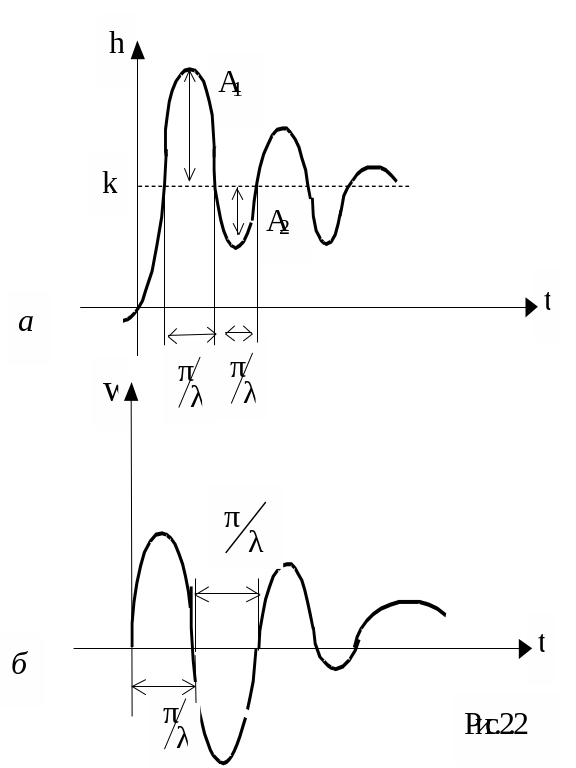
Переходная и весовая характеристики этого звена выражаются следующими формулами и представлены на рис.2.2:

На рис.2.2a: .

a.5. Консервативное звено

Является частным случаем колебательного звена при

.

Его переходная характеристика представляет незатухающие колебания:

a.6. Звено чистого запаздывания

Его можно отнести к позиционным условно, т.к. оно является достаточно упрощенной идеализацией. Такое звено можно описать передаточной функцией

.

Оно соответствует реальным объектам, которые передают входной сигнал совершенно точно, но с постоянной задержкой по времени τ. Таким образом, можно описать поведение конвейерной линии (по передачи материала или информации) или устройства временной задержки. Это звено имеет переходную и весовую характеристики такие же, как и безынерционное звено, но смещенные по оси времени на величину τ.

2. Интегрирующие звенья

b.1. Идеальное интегрирующее звено

Это звено описывается дифференциальным уравнением:

и имеет передаточную функцию

.

Примеры интегрирующего звена: операционный усилитель с емкостью в обратной связи (рис.2.3), электродвигатель постоянного тока, если управляющее напряжение – входная величина, а угол поворота – выходная.

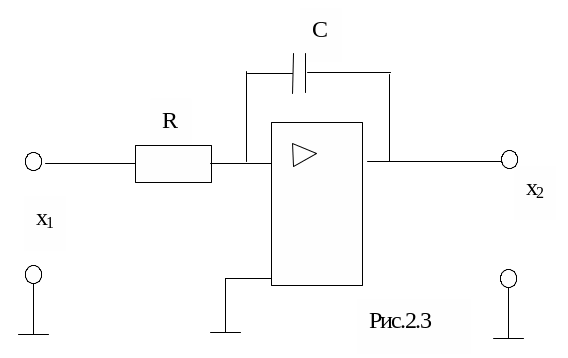
Переходная характеристика интегрирующего звена - прямая, которая неограниченно возрастает во времени, угол ее наклона равен коэффициенту k

h(t)=kt 1(t);

весовая функция

w(t)=k 1(t)=const.

b.2. Интегрирующее звено с замедлением

Дифференциальное уравнение:

.

Передаточная функция: ,

которую удобно представить последовательностью двух динамических звеньев:

;

;

.

b.3. Изодромное звено:

Дифференциальное уравнение:

.

Передаточная функция

.

Для изодромного звена:

.

3. Дифференцирующие звенья

c.1. Идеальное дифференцирующее звено.

Дифференциальное уравнение

.

Передаточная функция

Таким образом, это звено выдает производную от функции времени входного сигнала:

.

Примером идеального дифференцирующего звена может служить тахогенератор, выходное напряжение которого пропорционально входной скорости вращения. Это звено имеет постоянную фазовую характеристику, равную ( ).

c.2. Дифференцирующее звено с замедлением

Дифференциальное уравнение: .

Передаточная функция: ,

которая может быть представлена последовательным соединением идеального дифференцирующего и апериодического звеньев.

Вообще говоря, любая сложная передаточная функция линейной системы может быть выражена через комбинацию следующего множества элементарных звеньев:

.

При исследовании систем автоматического регулирования их удобно представлять в виде структурных схем (блок-схем), на которых выделены отдельные динамические звенья с соответствующими передаточными функциями и связями между ними, которые показывают направление передачи сигналов. Как правило, каждое звено имеет один входной и один выходной сигнал.

Помимо звеньев на блок-схемах обозначаются также узлы (места разветвления сигналов) и сумматоры, объединяющие два и более входных сигналов в один выходной. Сумматор изображается в виде круга, разделенного на секторы, причем если входной сигнал инвертируется на входе сумматора, то соответствующий сектор заштриховывается. Знак минус может также быть написан рядом с соответствующим входом.

Пример блок-схемы приведен на рис.2.4.

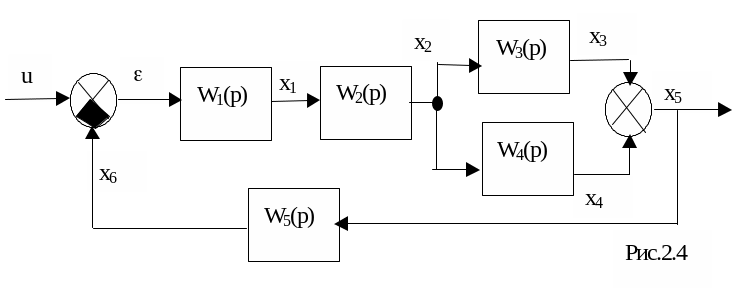
На данной схеме имеют место наиболее распространенные типы соединения динамических звеньев: последовательное, параллельное и соединение с обратной связью.

Преобразование блок-схем линейных систем автоматического регулирования (преобразование передаточных функций) производится в соответствии с тремя основными правилами:

1. Если звенья соединены последовательно, то результирующая передаточная функция получается как произведение передаточных функций этих звеньев.

2. Если звенья соединены параллельно, то результирующая передаточная функция получается как сумма передаточных функций этих звеньев.

Это вытекает из принципа суперпозиции для линейных систем. В соответствии с первыми двумя правилами можно преобразовать блок-схему (рис.2.4) к следующему виду (рис. 2.5).

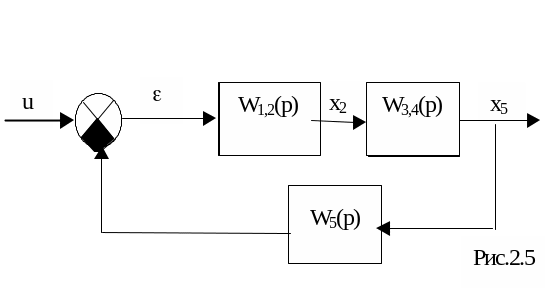
где W_1,2(p)=W₁(p) W₂(p).

W_3,4(p)=W₃(p)+W₄(p).

3. Для соединения звеньев с обратной связью результирующая передаточная функция получится в виде

где - передаточная функция прямой цепи;

- передаточная функция обратной цепи. (рис.2.6).

В выражении (1) знак “минус” будет, если в системе организована положительная обратная связь, знак “плюс” - если отрицательная.

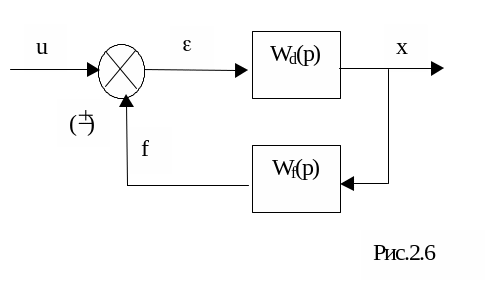
Например, систему, изображенную на рис.2.5, можно преобразовать к одной результирующей передаточной функции:

Если а тогда

Часто необходимо получить передаточную функцию замкнутой системы, зная передаточную функцию разомкнутой системы , когда функция обратной связи единичная W_f(p)=1. В этом случае

При исследовании систем часто возникает задача преобразования структурных схем для более удобного их представления или для выявления путей возможного улучшения качеств. Требуется, например, перенести то или иное звено в другую часть структуры. В соответствии с принципом суперпозиции для линейных систем мы можем использовать несколько дополнительных свойств, позволяющих получать блок-схемы эквивалентные исходным:

1) Перенос узла с выхода на вход сумматора (рис.2.7):

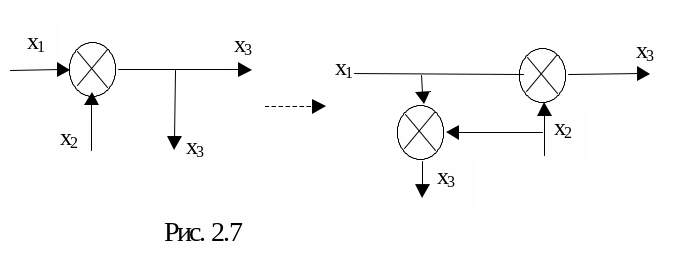
2) Перенос узла со входа на выход сумматора (рис.2.8):

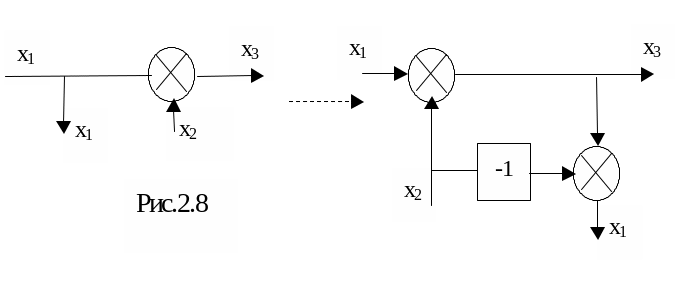
3 ) Перенос узла с выхода на вход звена (рис.2.9):

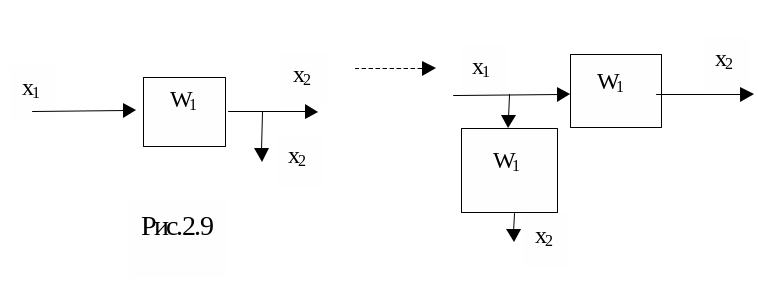4) Перенос узла со входа на выход звена (рис.2.10):

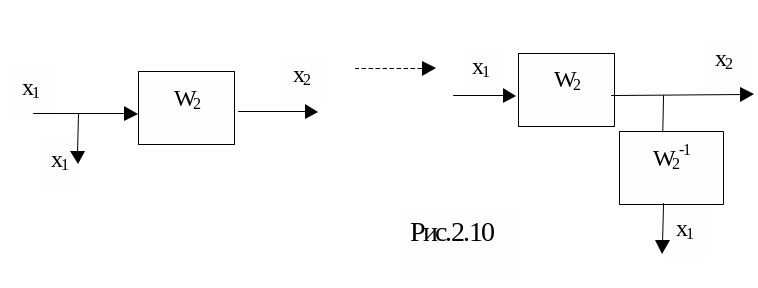
5) Перенос сумматора с выхода на вход звена (рис.2.11):

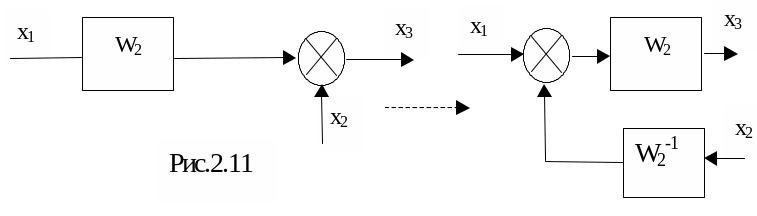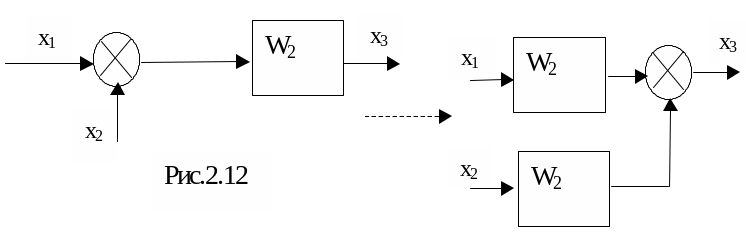
6) 6)Перенос сумматора со входа на выход звена (рис.2.12):

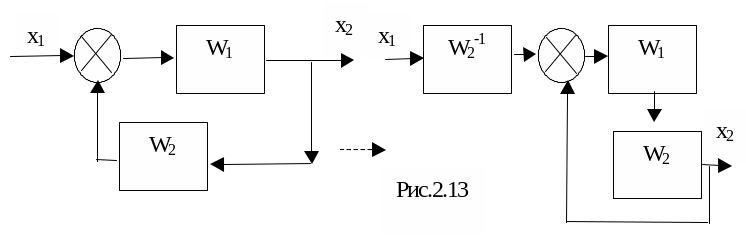
7) Преобразование к единичной обратной связи (рис.2.13):

Пример:

Преобразование блок-схемы (рис. 2.14a) к более простому виду (рис. 2.14b):

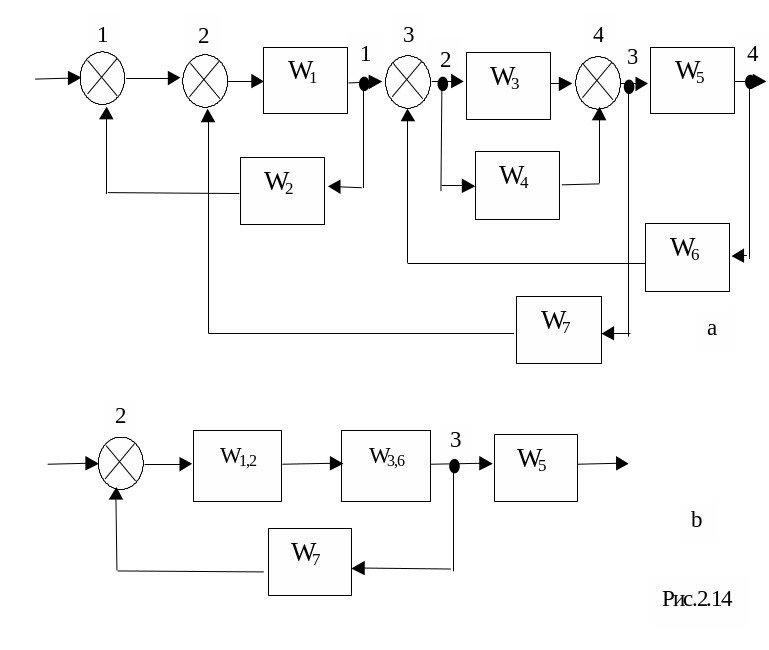
На рис.2.14b:

Для исследования динамических систем, модель которых представлена в виде структурной схемы система MatLab обладает мощным пакетом Simulink, который входит в базовый комплект поставки программного обеспечения. При вызове Simulink с помощью кнопки в основном окне MatLab происходит автоматическое открытие специального окна, в котором можно составлять исследуемую структуру системы из имеющегося набора стандартных звеньев. В набор входят звенья-источники сигналов, обычные линейные звенья, рассмотренные выше, нелинейные звенья различных типов, сумматоры и звенья для выполнения других операций над сигналами, виртуальные измерительные приборы для анализа сигналов.

Интерфейс пакета обладает интуитивной понятностью, поэтому специальных комментариев по его использованию не требуется. Наиболее важным пунктом меню Simulink является Simulation, с помощью которого задаются параметры моделирования: время, шаг дискретизации, диапазон отображения сигналов и т.п.

2.3. Варианты заданий на работу

При выполнении работы необходимо получить передаточную функцию и структурную схему одного из электротехнических объектов (по вариантам), после чего промоделировать ее в программе MatLab и сравнить с результатом предыдущей лабораторной работы:

1) Электродвигатель постоянного тока

2) Асинхронный электродвигатель переменного тока

3) Электрогенератор постоянного тока

4) Асинхронный генератор переменного тока

Числовые параметры системы задаются преподавателем или выбираются студентом самостоятельно.

2.4 Контрольные вопросы

1. Поясните смысл введения понятия элементарного динамического звена.

2. Назовите основные признаки, по которым классифицируются элементарные динамические звенья

3. Приведите физические аналоги апериодического и интегрирующего звеньев.

4. Какие общие свойства объединяют позиционные звенья?

5. Назовите инерционные звенья второго порядка. Приведите их физические аналоги и характеристики

6. Что такое передаточная функция звена?

7. Как отличить звено с интегрированием от позиционных?

8. Назовите основные правила построения и преобразования структурных схем.

9. Из каких элементов состоят структурные схемы линейных систем автоматического регулирования?

10. Чему равна результирующая передаточная функция последовательного соединения звеньев?

11. Чему равна результирующая передаточная функция соединения звеньев с отрицательной обратной связью?

12. Чему равна результирующая передаточная функция параллельного соединения звеньев?

13. Как перенести сумматор со входа на выход динамического звена?

14. Можно ли один сумматор разделить на два?

15. Что называется узлом структурной схемы системы регулирования?

16. Как перенести узел с выхода на вход динамического звена?

17. Для чего выполняются преобразования структурных схем?

Лабораторная работа 3

Построение частотных характеристик систем автоматического управления

3.1 Цель работы

Получить общее представление о различных частотных характеристиках динамических систем, об их роли в оценке качества процесса управления. Получить практические навыки в построении частотных характеристик различных типов.

3.2. Теоретические положения

Одним из важнейших классов динамических характеристик систем автоматического регулирования являются частотные характеристики. Частотные характеристики показывают результат воздействия на вход системы гармонического сигнала. Для систем регулирования прежде всего рассматривают две частотные характеристики – амплитудно-частотную (АЧХ) и фазочастотную (ФЧХ).

Амплитудно-частотная характеристика является функцией, связывающей амплитуду выходного (гармонического) сигнала системы с частотой этого воздействия (рис.3.1). Она показывает, во сколько раз увеличится (уменьшится) амплитуда синусоиды, прошедшей через систему.

Фазочастотная характеристика таким же образом связывает фазовое запаздывание на выходе с частотой синусоиды проходящей через систему. (рис.3.2).

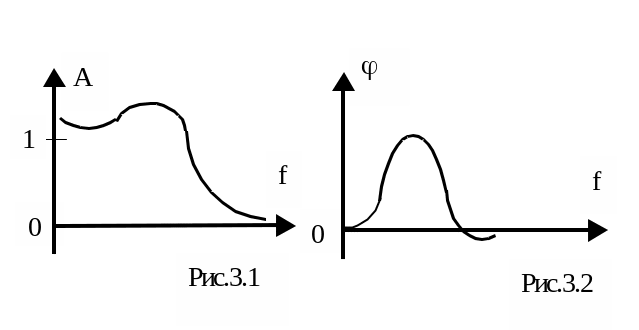
Частотные характеристики очень важны при изучении свойств систем управления, так как они показывают возможность системы передавать (воспроизводить, отрабатывать) сигналы с различными частотами, то есть показывают, как работает система в разных режимах

Довольно часто для представления частотных характеристик применяют логарифмическую шкалу, в которой по оси абсцисс откладывают величину lgω. (=2f – круговая частота ). Изменение  в 10 раз дает единицу по этой оси, которая называется декадой (dec).

По оси ординат АЧХ измеряется в децибелах (dB). Эта мера пропорциональна величине

20lgK,

где - коэффициент усиления (отношение амплитуды выходного гармонического сигнала к амплитуде входного). Таким образом, логарифмическая АЧХ (ЛАЧХ) получается из АЧХ в линейном масштабе путем следующего преобразования:

L()=20lg|W(j )|=20lgA(). [dB].

Отрицательные значения L() соответствуют уменьшению амплитуды сигнала системой.

Логарифмическая фазочастотная характеристика (ЛФЧХ) отличается от обычной фазочастотной только логарифмическим масштабом частот.

Особенно важной чертой ЛАЧХ является то, что в логарифмическом масштабе АЧХ линейной системы может быть представлена в виде линейных асимптот, к которым довольно хорошо приближается реальная зависимость. Для ЛФЧХ каждая кривая, будучи смещенной вдоль оси частот, будет представлять множество других ФЧХ для систем с подобной структурой, но другими параметрами.

Ниже рассмотрим вид ЛАЧХ и ЛФЧХ для основных типов динамических звеньев, рассмотренных ранее.

1. Безынерционное звено: W(p)=K

L()=20lgK=const

()=0=const.

2. Апериодическое звено:

L_l() 20lgK – низкочастотная асимптота - прямая линия, параллельная оси частот.

L_h() 20lgK-20lgK-20lg - высокочастотная асимптота – прямая линия с углом наклона (-20db/dec).

Для того, чтобы найти частоту сопряжения этих асимптот объединим оба случая:

L_l()=L_h()

20lgK=20lgK-20lgT-20lg₀

ЛАЧХ и ЛФЧХ апериодического звена представлены на рисунке3.3.

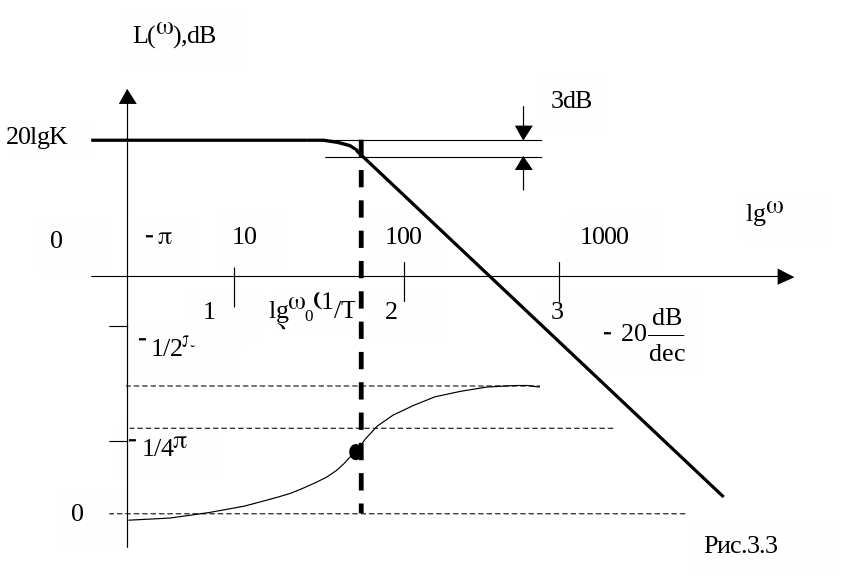
Для ФЧХ в линейном масштабе получим:

3.Колебательное звено:

Аналогично предыдущему:

Угол наклона асимптоты : (-40 dB/dec).

Частота сопряжения:

- называется резонансной (собственной) частотой звена:

ЛАФЧХ колебательного звена представлена на рис.3.4.

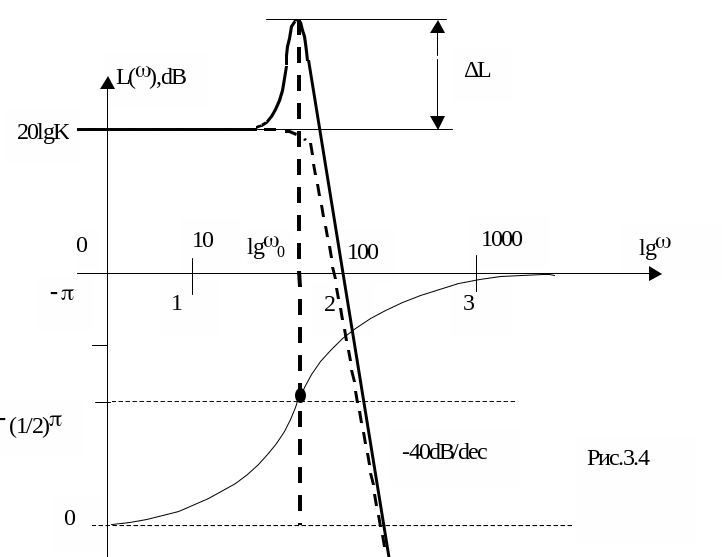
Величина пика L, соответствующего частоте сопряжения ₀ зависит от коэффициента демпфирования . Чем больше , тем меньше величина L. Для .=0 (случай консервативного звена) получим бесконечно большую величину резонансного пика АЧХ.

4. Интегрирующее звено

Легко найти, что

Для любого значения частоты ЛАЧХ этого звена будет абсолютно точно отображаться прямой с наклоном (–20 dB/dec):

Для =1 L()=20lgK;

L(10)=20lgK-20lg10=20lgK-20.

ФЧХ интегратора постоянна:

5. Дифференцирующее звено W(p)=Kp.

Аналогично доказывается, что L() для этого звена - прямая с наклоном (+20 dB/dec). Ее начальное значение для =1 L()=20lgK. ФЧХ также говорит о постоянном фазовом опережении

.

На основе изученных фактов можно вывести ряд правил для построения ЛАЧХ и ЛФХЧ.

Если передаточную функцию системы можно представить в виде:

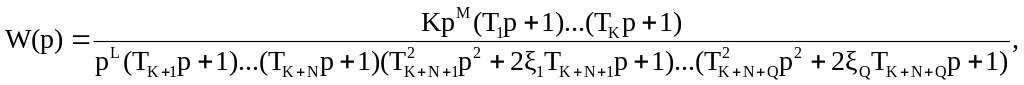
тогда общую ЛАФЧХ системы можно построить как геометрическую сумму ЛАФЧХ элементарных звеньев входящих в произведение (последовательно соединенных).

Начальная точка ЛАЧХ выбирается из условия L()=20lgK.

Наклон низкочастотной асимптоты равен величине 20(M-L) dB/dec. Целое число (M-L)=N далее будем называть порядком астатизма системы. Эта величина показывает как много имеется нулевых корней в знаменателе передаточной функции разомкнутой системы.

Далее на оси частот делаются отметки соответствующие частотам сопряжения всех звеньев. На каждом участке между отметками наклон асимптоты ЛАЧХ будет соответствовать сумме наклонов элементарных звеньев системы на данной частоте. Если частота , где T_j-постоянная времени апериодического звена - наклон будет иметь слагаемое (-20 dB/dec); для , где T_k – постоянная времени колебательного звена – в наклон добавляется компонента (-40 dB/dec).

Фазочастотная характеристика также строится как геометрическая сумма соответствующих ФЧХ элементарных звеньев.

Пример:

логарифмические частотные характеристики представлены на рис.3.5.

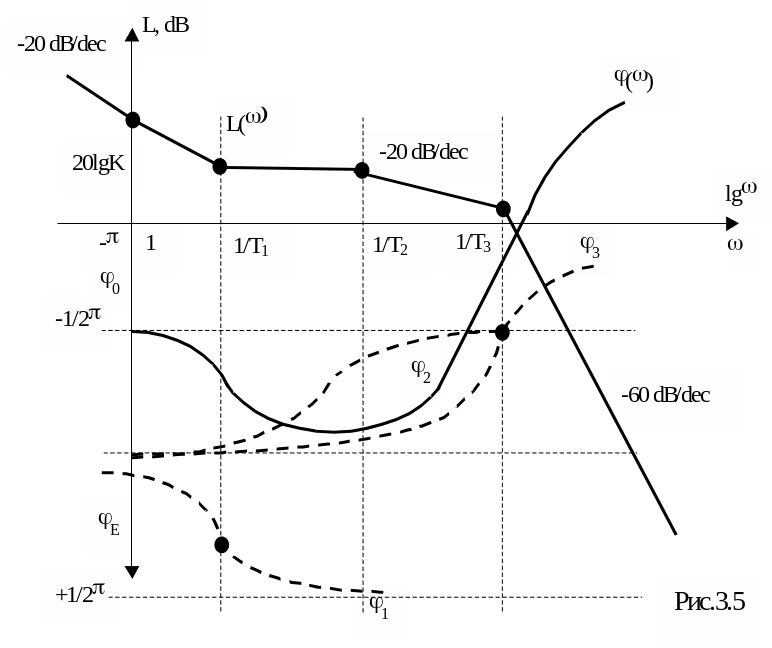
Д ругой формой частотных характеристик систем управления является комплексная амплитудно-фазовая ЧХ. Она имеет вид годографа: модуль описывающего вектора соответствует величине амплитудной характеристики на данной частоте, а аргумент (угол поворота) соответствует ФЧХ (рис.3.6)

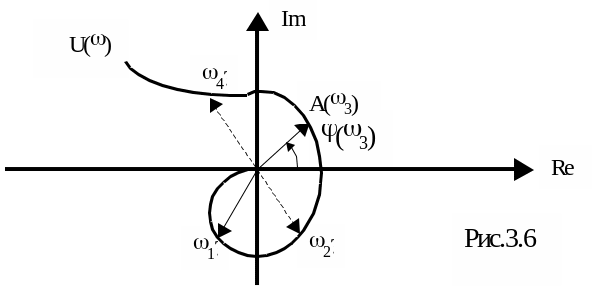
Иногда этот годограф представляют в виде совокупности двух характеристик P()=Re[U()] - (действительной АФЧХ) и Q()=Im[U()] (мнимой АФЧХ).

Все рассмотренные нами характеристики применяются преимущественно для линейных стационарных систем, так как только в этом классе систем характеристики постоянны для любого конечного значения амплитуды входного гармонического сигнала. (Выходная амплитуда будет здесь строго пропорциональна входному сигналу).

С целью получения графиков частотных характеристик в системе MatLab необходимо использовать рассмотренную в лабораторной работе №3 функцию plot.

Для использования логарифмических масштабов построения графиков предназначены функции semilogx, semilogy, loglog,особенности применения которых, как и для любой функции, можно узнать с помощью команды

help имя_функции

Также для получения комплексной АФЧХ системы можно использовать построение графиков в полярных координатах. Например, для этого можно воспользоваться последовательностью команд

phi=0: 0.01: 2*pi; r=sin(3*phi));

polar(phi, r).

3.3 Варианты заданий на работу

Постройте АЧХ и ФЧХ электротехнического объекта (по вариантам):

1) Электродвигатель постоянного тока

2) Асинхронный электродвигатель переменного тока

3) Электрогенератор постоянного тока

4) Асинхронный генератор переменного тока

Повторите построение этих характеристик в логарифмическом масштабе.

Числовые параметры системы задаются преподавателем или выбираются студентом самостоятельно.

4. Контрольные вопросы

1. Какие виды динамических характеристик вы знаете?

2. Какие основные характеристики используются для анализа систем управления?

3. Назовите основные частотные характеристики и дайте им физическую интерпретацию.

4. Что называется амплитудно-частотной характеристикой системы (звена)?

5. Что называется фазочастотной характеристикой системы (звена)?

6. Как определить выражение амплитудно-фазовой характеристики по заданной передаточной функции?

7. Что такое сопрягающая частота, частота среза , полоса пропускания системы (звена)?

8. Почему для построения частотных характеристик удобнее использовать логарифмическую шкалу?

9. В чем отличие ЛАФЧХ статических и астатических систем?

10. Какой начальный наклон имеет ЛАЧХ системы с астатизмом второго порядка?

Лабораторная работа 4

Оценка устойчивости линейных автоматических систем

4.1 Цель работы

Изучить методы анализа устойчивости линейных динамических систем. Получить практические навыки применения алгебраических и частотных критериев устойчивости.

4.2 Теоретические положения

Необходимым и достаточным условием устойчивости линейной динамической системы является отсутствие корней характеристического уравнения с положительными действительными частями. Чтобы установить справедливость этого условия нет необходимости вычислять все корни и даже составлять характеристическое уравнение. Для этого применяются критерии устойчивости, которые разделяются на алгебраические и частотные.

В качестве необходимого алгебраического условия устойчивости выступает то, что все коэффициенты характеристического полинома должны быть положительными (быть одного знака). Для нахождения достаточного условия требуется дополнительный анализ коэффициентов.

Критерий Гурвица. Этот критерий позволяет определить знак всех корней характеристического уравнения без их вычисления.

Пусть характеристический полином имеет вид:

Составим определитель Гурвица в виде:

и запишем его диагональные миноры

Последний определитель можно выразить через предпоследний:

По критерию Гурвица необходимым и достаточным условием устойчивости системы является выполнение следующей системы неравенств:

Используя этот критерий легко установить, что для систем первого и второго порядка необходимое условие является и достаточным:

Критерий Михайлова. Все частотные критерии устойчивости базируются на преобразовании Фурье (в передаточной функции выполняем подстановку ) и принципе аргумента, сущность которого заключается в следующем. С возрастанием частоты от ω=0 до ω=∞ характеристический вектор будет изменять свой аргумент (угол поворота относительно действительной оси ) в соответствии со знаком корня характеристического уравнения. Конец этого вектора будет описывать кривую, которая называется годографом Михайлова. Если в системе n-го порядка все n корней характеристического уравнения находятся слева от мнимой оси на комплексной плоскости, то характеристический вектор повернется на угол с возрастанием частоты от ω=0 до ω=∞. Следовательно, для устойчивости системы достаточно, чтобы при возрастании частоты от ω=0 до ω=∞ годограф Михайлова последовательно проходил n квадрантов на комплексной плоскости.

На рис.4.1 кривая Михайлова (a) соответствует устойчивой системе, кривая (b) – неустойчивой, система с годографом Михайлова (c) находится на колебательной границе устойчивости.

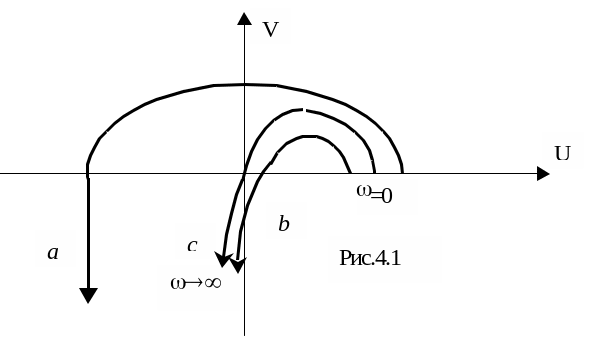
Критерий Найквиста. Часто необходимо определить устойчивость замкнутой системы управления с передаточной функцией Ф(р), если известна передаточная функция разомкнутой системы W(p)

,

здесь порядок полинома R(p) меньше, чем порядок полинома Q(p). (Передаточную функцию W(р) можно получить экспериментально).

Введем вспомогательную функцию

,

в числителе которой получим характеристический многочлен системы D(p).

Для устойчивой системы в диапазоне частот годограф не будет охватывать точку (0; j0). Следовательно, обычная комплексная частотная характеристика разомкнутой системы W(jω) не будет охватывать точку (-1; j0) на комплексной плоскости.

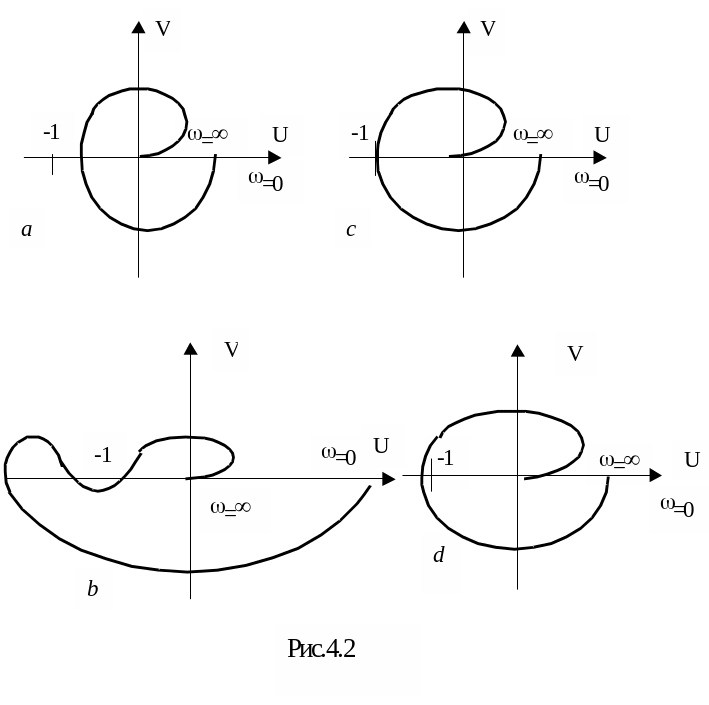
Поскольку две ветви частотной характеристики W(jω) (для и для ) симметричны относительно действительной оси, то для анализа устойчивости достаточно построить только первую ветвь. На рис.4.2a,b представлены характеристики W(jω) (годографы Найквиста) для устойчивой системы; на рис.4.2c – кривая W(jω) для системы, находящейся на колебательной границе устойчивости; на рис.4.2d – для неустойчивой системы.

Система, характеристика которой W(jω) представлена на рис.6.2a будет называться абсолютно устойчивой. Это значит, что при любом увеличении коэффициента усиления разомкнутой системы K замкнутая система останется устойчивой.

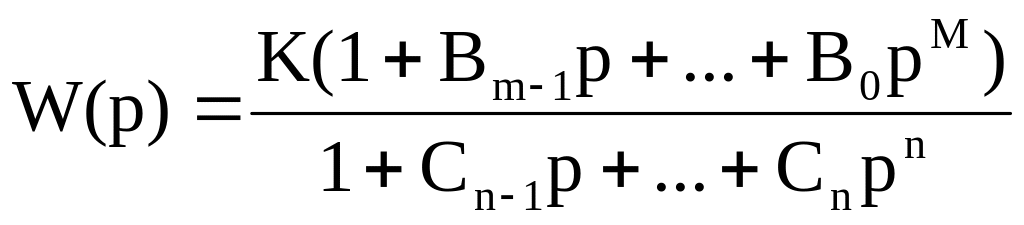
Если передаточная функция W(p) имеет астатизм порядка N, то при построении годографа Найквиста мы должны дополнить кривую дугами бесконечного радиуса с изменением аргумента на ( ) , чтобы начало годографа (для ) располагалось на положительной части действительной оси.

Иногда замкнутая система будет устойчивой даже если передаточная функция разомкнутой системы W(p) имеет корни знаменателя в правой части комплексной плоскости. Для этого случая критерий Найквиста имеет специальную форму. В графической форме это выражается в том, что годограф Найквиста должен охватывать точку (-1; j0) столько раз, сколько знаменатель W(p) имеет корней с положительной действительной частью.

Анализ устойчивости с помощью ЛАФЧХ. Требование критерия Найквиста, чтобы комплексная частотная характеристика разомкнутой системы не охватывала точку (-1; j0) на практике означает, что для частоты, где argW(jω) =( ), должно выполняться условие |W(jω) |<=1. В противном случае при замыкании системы можно получить условие самовозбуждения колебаний системы, когда сигнал отрицательной обратной связи превращается в положительную обратную связь, которая не уменьшает, а увеличивает рассогласование системы.

Таким образом, можно сказать, что для устойчивости системы необходимо, чтобы на частоте среза ω_с (где A(ω_с)=1) выполнялось условие φ(ω_с)>-. Наоборот, для частоты ω_π ( где φ(ω_π)=-π) должно выполняться условие A( )<=1.

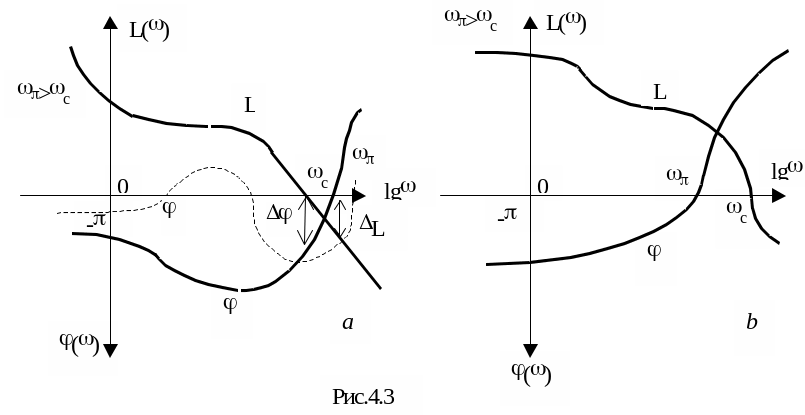
Если перевести эти условия в изображение логарифмической частотной характеристики, то получим, что при возрастании частоты ЛАЧХ L( ) должна пересекать отметку 0 dB до того, как ЛФЧХ φ(ω) пересечет отметку (- ) rad. На рис.4.3a построены логарифмические АЧХ и ФЧХ для устойчивой системы, на рис.4.3b – для неустойчивой. На рис.4.3a представлена также ФЧХ устойчивой системы, которая соответствует случаю, относящемуся по критерию Найквиста к рис.4.2b. Здесь за частоту ω_π следует принять последнюю точку пересечения линии φ(ω)=-π фазовой характеристикой при возрастании частоты.

Из рис.4.3b легко заключить, что для того, чтобы системы стала устойчивой необходимо уменьшить общий коэффициент усиления разомкнутой системы («опустив» кривую L(ω)).

Для устойчивой системы (рис.4.3a) можно определить запасы устойчивости по фазе Δφ и по амплитуде ΔL. Обычно для хорошей устойчивости автоматической системы предъявляются требования:

Применение критериев устойчивости к системам управления может быть выполнено с помощью системы MatLab, которую следует использовать для построения частотных характеристик, а также для вычисления определителя предварительно заданной квадратной матрицы X с помощью функции det[X]. Для применения частотных критериев используются рассмотренные в предыдущей лабораторной работе функции построения графиков в линейных, логарифмических или полярных координатах.

4.3 Варианты заданий на работу

Определить устойчивость замкнутой системы автоматического регулирования, включающей в качестве объекта управления одну из электрических машин (по вариантам):

1) Электродвигатель постоянного тока

2) Асинхронный электродвигатель переменного тока

3) Электрогенератор постоянного тока

4) Асинхронный генератор переменного тока

Устойчивость вначале определяется по критерию Гурвица, а затем по одному из частотных критериев, указанному преподавателем. Числовые параметры системы задаются преподавателем или выбираются студентом самостоятельно.

4. Контрольные вопросы

1. К чему сводятся условия устойчивости линейной динамической системы?

2. Сформулируйте необходимое алгебраическое условие устойчивости.

3. Как проверяется устойчивость системы с помощью алгебраических критериев? В чем их достоинство?

4. На каком принципе основаны все частотные критерии устойчивости? Объясните этот принцип.

5. Нарисуйте годограф Михайлова устойчивой системы четвертого порядка.

6. Каковы преимущества частотных критериев устойчивости?

7. Может ли неустойчивая разомкнутая динамическая система при замыкании обратной связи стать устойчивой?

8. Нарисуйте годограф Найквиста устойчивой системы с астатизмом второго порядка.

9. Поясните, как отразится на устойчивости системы регулирования последовательное включение интегрирующего регулятора.

10. Как определить устойчивость замкнутой системы по ЛАФЧХ разомкнутой системы?

Лабораторная работа 5

Исследование точности работы автоматических систем

5.1 Цель работы

Изучить методы анализа точности систем автоматического управления. Получить практические навыки вычисления установившейся ошибки в линейной системе при заданном входном воздействии.

5.2 Теоретические положения

Под точностью автоматической системы понимают степень приближения выходной величины к ее заданному значению. Точность оценивается ошибкой х, равной

x= g – x_ос

где g – заданное значение входной (регулируемой) величины, x_ос - действительное значение регулируемой величины в системе, представленной на рис. 5.1

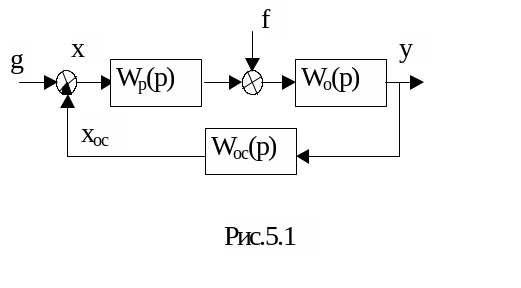
В случае отсутствия погрешностей в звеньях системы общая установившаяся статическая ошибка по теореме о конечном значении в преобразовании Лапласа определится по выражению

x = {Ф_x(p)G(p) + Ф_fx(p)F(p)}|_p=0,

где Ф_x(p) и Ф_fx(p) – передаточные функции замкнутой системы по ошибке от управляющего и возмущающего воздействий соответственно;

G(p) и F(p) – изображения управляющего и возмущающего воздействий.

С точки зрения принципа суперпозиции возмущающее воздействие f(t) и управляющее воздействие g(t) действуют на линейную систему независимо, поэтому можно упрощенно рассматривать одно внешнее воздействие g(t) и одну передаточную функцию разомкнутой системы W(p)=W_p(p) W_o(p) W_oc(p) приняв f(t)=0. Тогда изображение ошибки равно

где - передаточная функция замкнутой системы по ошибке.