§5. Остовные деревья минимальной стоимости.

5.1. Определения и свойства.

Определение 1. Свободным деревом называется связный граф без циклов.

Остовным деревом графа 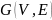называется свободное дерево , , 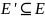содержащее все вершины графа .

Теорема 1. (Свойства свободных деревьев)

1. Каждое свободное дерево, имеющее n вершин (n≥1), имеет ровно n-1 ребро.

2. При добавлении в любое свободное дерево нового ребра образуется цикл.

Определение 2. Пусть - помеченный граф, для каждого ребра его метка (стоимость) равна 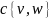. Стоимостью остовного дерева графа называется сумма стоимостей всех ребер, входящих в дерево. То есть

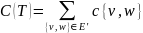
В этом разделе рассматриваются методы нахождения остовных деревьев минимальной стоимости.

Типичное применение остовных деревьев минимальной стоимости можно найти при разработке коммуникационных сетей. Здесь вершины графа представляют города, ребра - возможные коммуникационные линии между городами, а стоимость ребер соответствует стоимости коммуникационных линий. В этом случае остовное дерево минимальной стоимости представляет коммуникационную сеть, объединяющую все города коммуникационными линиями минимальной стоимости.

Теорема 2. (Свойство остовных деревьев минимальной стоимости).

Пусть 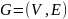— связный граф с заданной функцией стоимости, определенной на множестве ребер. Обозначим через 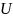подмножество множества вершин . Если 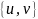— такое ребро наименьшей стоимости, что 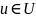и 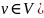, тогда для графа существует остовное дерево минимальной стоимости, содержащее ребро .

Доказательство. Допустим противное: не существует остовного дерева минимальной стоимости для графа , содержащего , то есть для любого остовного дерева 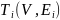, содержащего его стоимость не минимальна.

Рассмотрим произвольное остовное дерев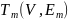о , имеющее минимальную стоимость. В частности, для него

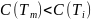(1)

Добавим к дереву 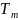ребро , получим 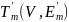, 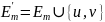. По теореме 1(2), 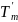- граф с циклом. Цикл содержит ребро , соединяющее и 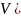, а также некоторое ребро 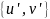, соединяющее и . (рис. 5.1.1)

Причем, по выбору ребра , справедливо .

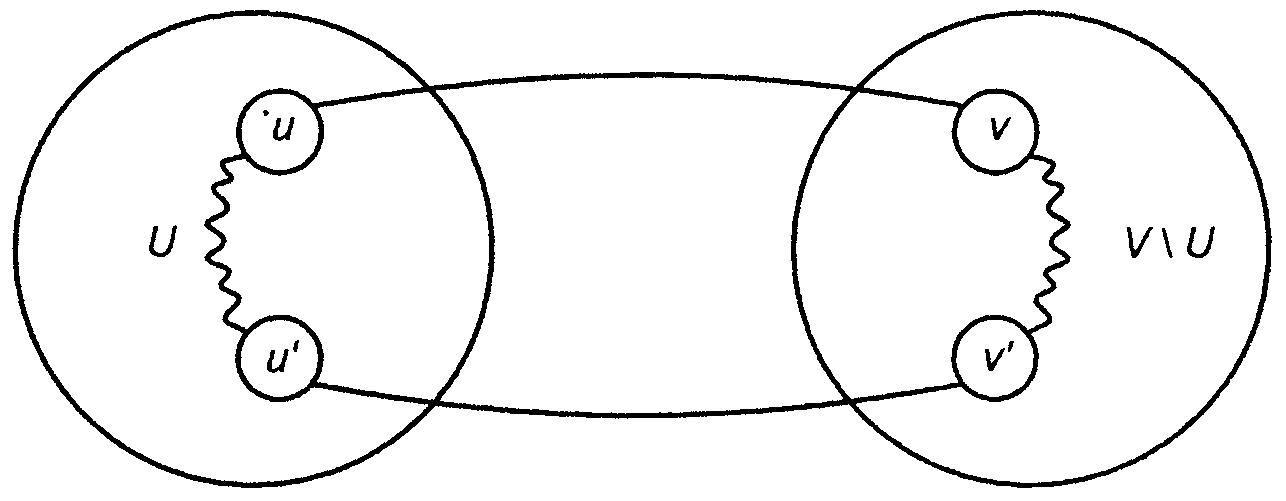Рис. 5.1.1.

Удалим ребро из дерева , получим , .

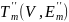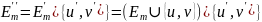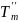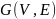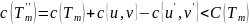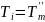Так как удаление ребра привело к разрыву цикла, то - свободное дерево, содержащее все вершины , следовательно - остовное дерево графа , содержащее , стоимость которого . Однако, выбирая в (1) , получим 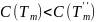. Противоречие. Значит допущение неверно. Теорема доказана.

Существуют различные способы построения остовных деревьев минимальной стоимости. Многие из них основаны на теореме 2. Далее будут рассмотрены два таких алгоритма.

5.2. Алгоритм Прима.

Пусть дан граф , 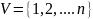. Множество вершин , входящих в остовное дерево минимальной стоимости, строится в алгоритме Прима (Prim) по следующим правилам:

1. Сначала состоит из одной произвольной вершины. Например, .

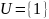2. На каждом шаге алгоритма находится ребро наименьшей стоимости 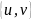такое, что и . Ребро добавляется к дереву, вершина переносится из множества во множество .

Согласно теореме 2, существует остовное дерево минимальной стоимости графа , содержащее новое множество вместе с ребром .

3. Шаг 2 повторяется до тех пор, пока множество не станет равным множеству , то есть, пока не будет достигнуто 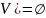. Это означает, что в остовное дерево будут включены все вершины графа и некоторые его ребра. По теореме 2, существует остовное дерево минимальной стоимости графа , содержащее именно те ребра, которые выбирались на шаге 2. Значит, полученное остовное дерево и является остовным деревом минимальной стоимости.

Эскиз алгоритма показан в листинге 5.2.1.

Листинг 5.2.1. Эскиз алгоритма Прима

procedure Prim ( G: граф; var T: множество ребер );

var

U: множество вершин;

u, v: вершина;

begin

T:= ;

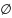U:= {1};

while U 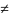V do begin

нахождение ребра (u, v) наименьшей стоимости и такого,

что и ;

Т:= Т ;

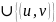U:= U

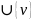
end

end; { Prim }

Для выбора ребра с наименьшей стоимостью, соединяющего множества и на каждом шаге алгоритма используются два массива. Массив CLOSEST[i] для каждой вершины i из множества содержит вершину из , с которой она соединена ребром минимальной стоимости (это ребро выбирается среди ребер, инцидентных вершине i, и которые ведут в множество ). Другой массив LOWCOST[i] хранит значение стоимости ребра (i, CLOSEST[i]).

На каждом шаге алгоритма просматривается массив LOWCOST, находится минимальное значение LOWCOST[k] (строки (5)-(10)). Вершина k принадлежит множеству и соединена ребром с вершиной из множества . Затем выводится на печать ребро (k, CLOSEST[k]) (строка (11)).

После нахождения очередной вершины k остовного дерева значение LOWCOST[k] устанавливается равным infinity (бесконечность), очень большому числу, такому, чтобы эта вершина уже в дальнейшем не рассматривалась (строка (12)). Значение числа infinity должно быть больше стоимости любого ребра графа.

Так как вершина k присоединяется к множеству , то вследствие этого изменяются массивы LOWCOST и CLOSEST (строки (13)-(16)).

Программа на языке Pascal, реализующая алгоритм Прима, представлена в листинге 5.2.2. На вход программы поступает матрица стоимостей ребер графа - массив С размера , чьи элементы C[i, j] равны стоимости ребер 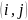. Если ребра не существуют, то элемент C[i, j] полагается равным некоторому достаточно большому числу.

Листинг 5.2.2. Программа выполнения алгоритма Прима

procedure Prim ( С: аггау[1..n, 1..n] of real );

{ Prim печатает ребра остовного дерева минимальной стоимости

для графа с вершинами {1, ..., n} и матрицей стоимости С}

var

LOWCOST: array[1..n] of real;

CLOSEST: array[1..n] of integer;

i, j, k, min: integer;

{ i и j — индексы. При просмотре массива LOWCOST

к — номер найденной вершины, min = LOWCOST[k] }

begin

(1) for i:= 2 to n do begin

{ первоначально в множестве U только вершина 1 }

(2) LOWCOST[i]:= СП, i];

(3) CLOSEST[i]:= 1

end;

(4) for i:= 2 to n do begin { поиск вне множества U наилучшей вершины к, имеющей

инцидентное ребро, оканчивающееся в множестве U }

(5) min:= LOWCOST[2];

(6) k:= 2;

(7) for j:= 3 to n do

(8) if LOWCOST[j] < min then begin

(9) min:= LOWCOST[j];

(10) k:= j

end;

(11) writeln{k, CLOSEST[k]); { вывод ребра на печать }

(12) LOWCOST[k] := infinity; { к добавляется в множество U }

(13) for j:= 2 to n do { корректировка стоимостей в U }

(14) if (C[k, j] < LOWCOST[j]) and

(LOWCOST[j] < infinity) then begin

(15) LOWCOST[j]:= C[k, j];

(16) CLOSEST[j]:= k

end

end

end; { Prim }

Пример. Рассмотрим этапы построения остовного дерева минимальной стоимости для графа на рис. 5.2.1.

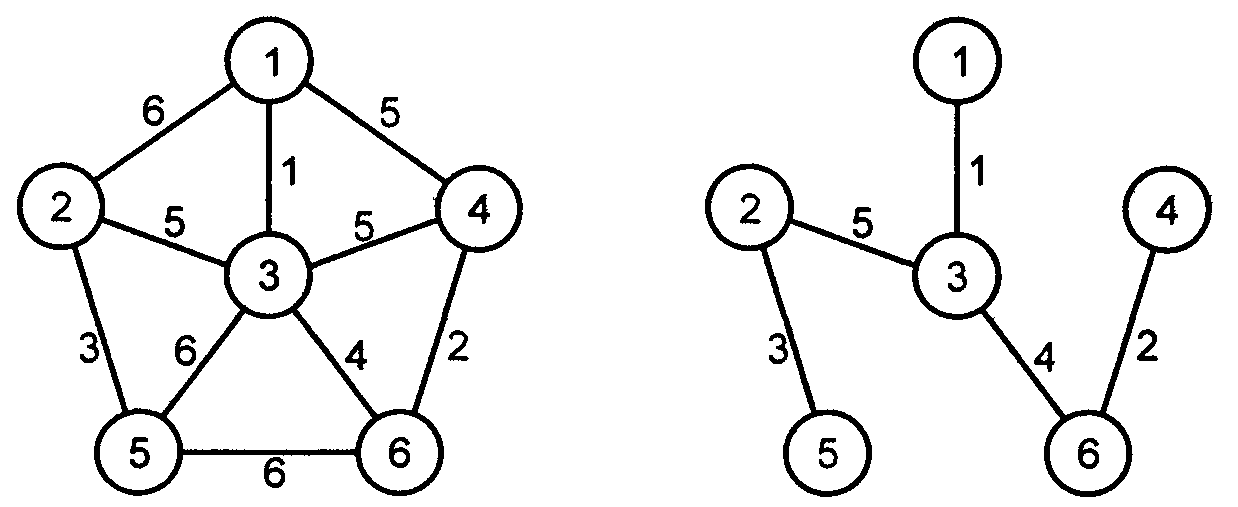Рис. 5.2.1.

Решение. Результаты последовательных итераций приведем в таблице

Множество U	Ребро {u, v}	Стоимость с{u,v}	Вершина v
{1}	{1,3}	1	3
{1,3}	{3,6}	4	6
{1,3,6}	{6,4}	2	4
{1,3,6,4}	{3,2}	5	2
{1,3,6,4,2}	{2,5}	3	5
{1,3,6,4,2,5} = V

Этапы построения остовного дерева минимальной стоимости изображены на рис. 5.2.2.

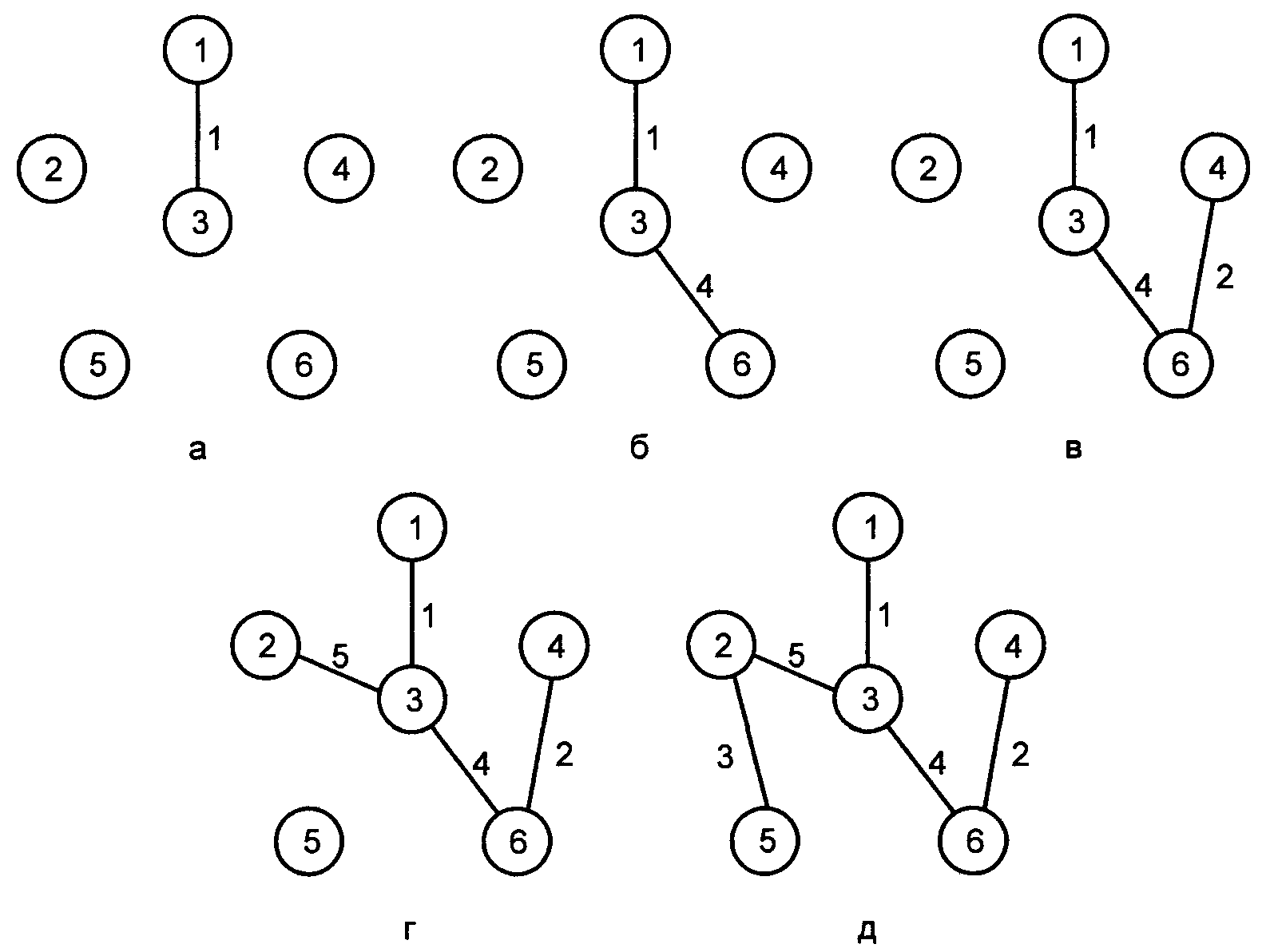Рис.5.2.2

Время выполнения алгоритма Прима имеет порядок , поскольку выполняется 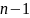итерация внешнего цикла строк (4) – (16), а каждая итерация этого цикла требует времени порядка 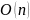для выполнения внутренних циклов в строках (7)-(10) и (13)–(16). Если значение достаточно большое, то использование этого алгоритма нерационально.

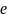Далее мы рассмотрим алгоритм Краскала нахождения остовного дерева минимальной стоимости, который выполняется за время порядка , где — количество ребер в данном графе. Если значительно меньше , то алгоритм Краскала предпочтительнее, но если близко к , рекомендуется применять алгоритм Прима.