4.2. Алгоритм Флойда.

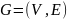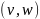Рассмотрим общую задачу поиска кратчайших путей между всеми парами узлов в помеченном ориентированном графе . Для любой упорядоченной пары узлов требуется найти путь из 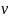в 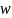наименьшей стоимости.

Первый способ заключается в применении алгоритма Дейкстры, выбирая поочередно каждый узел орграфа в качестве источника. Пусть n=|V|. Временная сложность алгоритма Дейкстры O(n²). Применяя его в цикле для каждого из n узлов, получим временную сложность алгоритма O(n³).

Второй способ заключается в применении алгоритма, известного как алгоритм Флойда-Варшалла (Floyd-Warshall algorithm) или алгоритма Флойда. Временная сложность его в худшем случае также равна O(n³).

Как и ранее, наличие в орграфе дуг с отрицательным весом допускается, но предполагается, что контуры с отрицательным весом отсутствуют.

Структура кратчайшего пути

В алгоритме Флойда рассматриваются "промежуточные" узлы кратчайшего пути. Промежуточным узлом простого пути 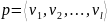называется произвольный узел, отличный от и 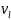т.е. это любой узел из множества .

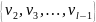Предположим, что орграф 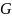состоит из узлов . Рассмотрим подмножество узлов 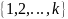для некоторого 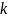. Для произвольной пары узлов 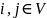рассмотрим все пути из узла 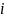в узел 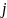, все промежуточные узлы которых выбраны из множества . Пусть среди этих путей 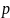— путь с минимальным весом (этот путь простой). В алгоритме Флойда используется взаимосвязь между путем р и кратчайшими путями из узла в узел , все промежуточные узлы которых принадлежат множеству . Эта взаимосвязь зависит от того, является ли узел k промежуточным на пути .

Если — не промежуточный узел пути , то все промежуточные узлы этого пути принадлежат множеству . Таким образом, кратчайший путь из узла в узел со всеми промежуточными узлами из множества одновременно является кратчайшим путем из узла в узел со всеми промежуточными узлами из множества .

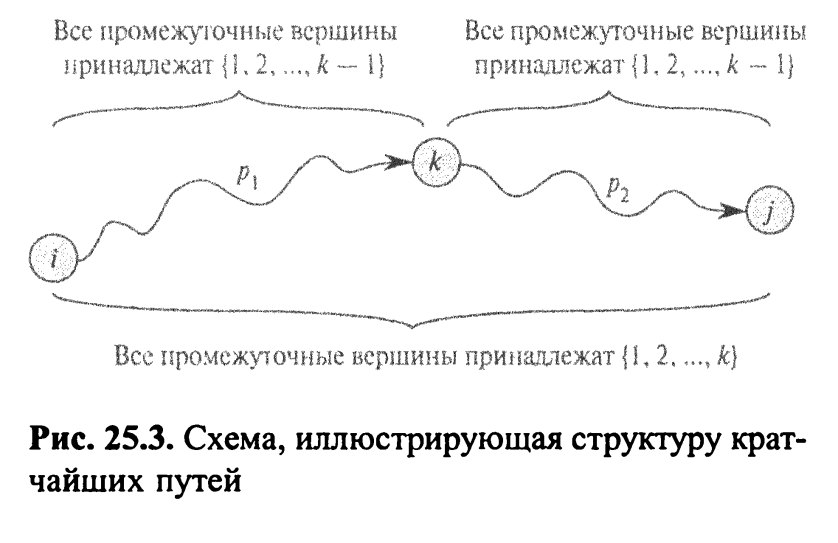Рис.4.2.1.

Если — промежуточный узел пути , то этот путь, как видно из рис. 4.2.1, можно разбить следующим образом: 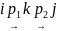. Поскольку не является промежуточным узлом пути 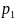, понятно, что —кратчайший путь из узла в узел , все промежуточные узлы которого принадлежит множеству . Аналогично, — кратчайший путь из узла в узел , все промежуточные узлы которого принадлежат множеству .

Вычисление весов кратчайших путей в восходящем порядке

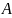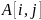Алгоритм Флойда использует матрицу размера , в которой элемент содержит длину кратчайшего пути из узла в узел , найденного к данной итерации. Используется также матрица , в которой элемент содержит последний узел, добавленный к пути из узла в узел к моменту текущей итерации.

Далее нижний индекс обозначает значение матрицы или P после -й итерации

Начальные значения на 0-й итерации: – вес дуги 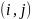для всех 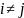. Таким образом, на начальном этапе кратчайшим путем из узла в узел считается непосредственно дуга , если она существует. На этом пути нет промежуточных узлов, поэтому . Если дуга 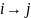отсутствует, то

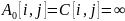
Кратчайший путь из узла в узел имеет, очевидно, стоимость 0, и не имеет промежуточных узлов, поэтому , .

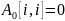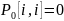Над матрицей выполняется 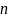итераций.

После 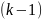-й итерации содержит наименьшую длину путей из узла в узел , которые могут проходить через узлы из множества и не проходят через узлы из множества .

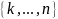На -й итерации для вычисления матрицы применяется следующая формула:

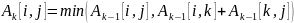
Графическая интерпретация этой формулы показана на рис 4.2.2.

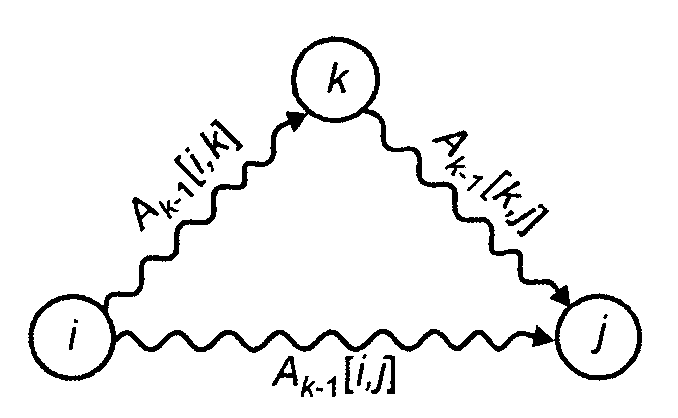
Рис. 4.2.2 Включение узла в путь от узла к узлу

Это означает, что для вычисления 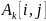проводится сравнение величины 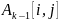(т.е. стоимость пути от узла к узлу без участия узла или другого узла с более высоким номером) с величиной 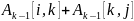(стоимость пути от узла до узла плюс стоимость пути от узла до узла ).

Если путь через узел дешевле, чем ,то величина заменяется на . При этом в матрице P фиксируется добавление к кратчайшему пути из узла в узел промежуточного узла : .

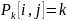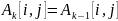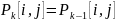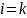В противном случае стоимость кратчайшего пути не меняется: и узел к пути не добавляется: . В частности, это всегда будет происходить при и при 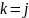, так как в этих случаях уже входит в путь и его включение, как промежуточного узла, не сократит стоимость. Таким образом, на -й итерации не меняются элементы -й строки и -го столбца матриц A и P.

Заметим, что поскольку кратчайший путь из узла в узел имеет, стоимость 0, и не имеет промежуточных узлов, то начальные значения диагональных элементов , не будут меняться в процессе итераций.

Пример.

1

2

8

3

5

2

3

Рис. 4.2.3 Помеченный ориентированный граф

На рис. 4.2.3 показан помеченный орграф, а далее представлены значения матриц А и P после трех итераций.

A0	1	2	3		P0	1	2	3		A1	1	2	3		P1	1	2	3
1	0	8	5		1	0	0	0		1	0	8	5		1	0	0	0
2	3	0	∞		2	0	0	0		2	3	0	8		2	0	0	1
3	∞	2	0		3	0	0	0		3	∞	2	0		3	0	0	0
A2	1	2	3		P2	1	2	3		A3	1	2	3		P3	1	2	3
1	0	8	5		1	0	0	0		1	0	7	5		1	0	3	0
2	3	0	8		2	0	0	1		2	3	0	8		2	0	0	1
3	5	2	0		3	2	0	0		3	5	2	0		3	2	0	0

Равенства 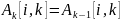и означают, что на -й итерации элементы матрицы , стоящие в -й строке и -м столбце, не изменяются.

Приведем примеры вычисления матриц A и P на различных итерациях алгоритма. Цветом выделены ячейки, значения которых подлежат пересчету на данной итерации.

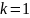
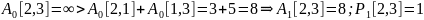
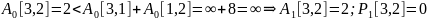
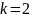
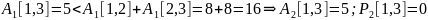
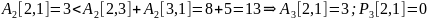
По окончательным значениям матриц A₃ и P₃ восстановим кратчайшие пути и их стоимости.

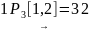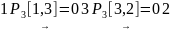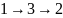От узла 1 до узла 2: , . Кратчайший путь , его стоимость .

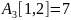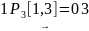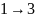От узла 1 до узла 3: . Кратчайший путь , его стоимость .

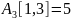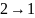От узла 2 до узла 1: . Кратчайший путь , его стоимость .

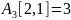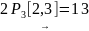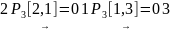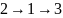От узла 2 до узла 3: , . Кратчайший путь , его стоимость .

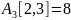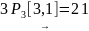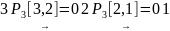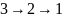От узла 3 до узла 1: , . Кратчайший путь , его стоимость .

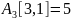Листинг 4.2.1. Реализация алгоритма Флойда

procedure Floyd( var A: array[1..n, 1..n] of real; С: array[l..n, 1..n] of real);

var

i, j, k: integer;

begin

for i: = 1 to n do

for j: = 1 to n do begin

A[i, j] := C[i, j];

P[i, j] := 0;

end;

for i := 1 to n do

A[i , i] := 0;

for k: = 1 to n do

for i: = 1 to n do

for j: = 1 to n do

if A[I,k] + A[k, j] < A[I, j] then begin

A[I, j] := A[I, k] + A[k, j];

P[I, j] := k;

end;

end; { Floyd}

Для вывода на печать последовательности узлов, составляющих кратчайший путь от узла до узла , вызывается процедура path(i,j), код которой приведен в листинге 4.2.2.

Листинг 4.2.2. Процедура печати кратчайшего пути

procedure раth ( i, j: integer );

var

k: integer ;

begin

k:= P[i, j];

if k = 0 then

return;

path(i, k);

writeln(k);

path(k, j)

end; { path }

Сравнение алгоритмов Флойда и Дейкстры

Ввиду наличия трех вложенных циклов (см. листинг 4.2.1), временная сложность алгоритма Флойда равна .

Поскольку версия алгоритма Дейкстры с использованием матрицы смежности находит кратчайшие пути от одного узла за время порядка , то в этом случае применение алгоритма Дейкстры для нахождения всех кратчайших путей потребует времени порядка , т.е. получим такой же временной порядок, как и в алгоритме Флойда.

Константы пропорциональности в порядках времени выполнения для обоих алгоритмов зависят от применяемых компилятора и вычислительной машины, а также от особенностей реализации алгоритмов. Вычислительный эксперимент и измерение времени выполнения — самый простой путь подобрать лучший алгоритм для конкретного приложения.

Если 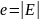, количество дуг в орграфе, значительно меньше, чем 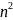, тогда, несмотря на относительно малую константу в выражении порядка для алгоритма Флойда, целесообразно применять версию алгоритма Дейкстры со списками смежности. В этом случае время решения общей задачи нахождения кратчайших путей имеет порядок , что значительно лучше алгоритма Флойда, по крайней мере, для больших разреженных графов.

Транзитивное замыкание

Во многих задачах интерес представляет только сам факт существования пути, длиной не меньше единицы, от узла до узла . Алгоритм Флойда можно приспособить для решения таких задач. Полученный в результате алгоритм еще до Флойда разработал Уоршелл (S. Warshall), поэтому его также называют алгоритмом Уоршелла.

Предположим, что матрица стоимостей 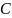совпадает с матрицей смежности для данного орграфа , т.е. 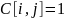только в том случае, если есть дуга , и 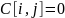, если такой дуги не существует. Требуется вычислить матрицу такую, что тогда и только тогда, когда существует путь от узла до узла длиной не менее 1 и 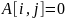— в противном случае. Такую матрицу часто называют транзитивным замыканием матрицы смежности.

Транзитивное замыкание можно вычислить с помощью процедуры, подобной Floyd, применяя на k-м шаге следующую формулу к булевой матрице :

.

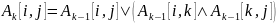Эта формула устанавливает, что существует путь от узла до узла , проходящий через узлы с номерами, не превышающими , только в следующих случаях.

1. Уже существует путь от узла до узла , который проходит через узлы с номерами, не превышающими .

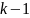2. Существует путь от узла до узла , проходящий через узлы с номерами, не превышающими , и путь от узла до узла , который также проходит через узлы с номерами, не превышающими .

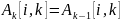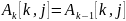Здесь, как и в алгоритме Флойда, и , то есть на -й итерации элементы матрицы , стоящие в -й строке и -м столбце, не изменяются. В отличие от алгоритма Флойда, для поиска пути длиной не меньше 1 от узла до узла на каждой итерации производится пересчет в том числе и диагональных элементов матрицы А.

Пример. Последовательные итерации при получении А₃ - транзитивного замыкания матрицы смежности орграфа из рис. 4.2.3.

A0	1	2	3		A1	1	2	3
1	0	1	1		1	0	1	1
2	1	0	0		2	1	1	1
3	0	1	0		3	0	1	0

A2	1	2	3		A3	1	2	3
1	1	1	1		1	1	1	1
2	1	1	1		2	1	1	1
3	1	1	1		3	1	1	1

Программа Warshall вычисления транзитивного замыкания показана в листинге 4.2.3.

Листинг 4.2.3. Программа Warshall для вычисления транзитивного замыкания

procedure Marshall ( var A: array[l..n, l..n] of boolean; C: array[l..n, l..n] of boolean );

var

i, j, k: integer;

begin

for i:= 1 to n do

for j-.= 1 to n do

A[i, j]:= C[i, j];

for k:= 1 to n do

for i:= 1 to n do

for j:= 1 to n do

if A[i, j] = false then

A[i, j] := A[i, k] and A[k, j]

end; { Warshall }