§4. Нахождение кратчайшего пути.

4.1. Алгоритм Дейкстры.

Пусть дан неориентированный (ориентированный) взвешенный граф с вершинами и рёбрами. Веса всех рёбер неотрицательны. Указана некоторая стартовая вершина , называемая источником. Рассмотрим задачу нахождения длины кратчайших путей из вершины во все остальные вершины, а также способ вывода самих кратчайших путей. Под длиной пути понимается сумма стоимостей ребер, составляющих путь.

Эта задача называется "задачей о кратчайших путях с единственным источником" (single-source shortest paths problem).

Далее рассмотрим алгоритм, который предложил датский исследователь Дейкстра (Dijkstra) в 1959 г. Алгоритм формулируется для неориентированного графа. Случай, когда данный граф ориентированный, рассматривается аналогично (см. пример 1).

В массиве , для каждой вершины будет храниться текущая длина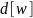 , кратчайшего пути из в .

Кроме того, для каждой вершины в булевском массиве будет храниться информация, помечена она или нет.

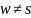В массиве предков для каждой вершины хранится номер вершины , являющейся предпоследней в кратчайшем пути до вершины .

Начало (нулевая итерация). Изначально , а для всех остальных вершин эта длина равна бесконечности (обычно в качестве бесконечности выбирают достаточно большое число, заведомо большее возможной длины пути):

Для массива предков принимаются следующие начальные значения

Изначально все вершины не помечены, и множество помеченных вершин S=.

Алгоритм Дейкстры состоит из итераций.

На очередной i-ой итерации выбирается вершина с наименьшей величиной 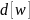среди ещё не помеченных, т.е.:

(Понятно, что на первой итерации выбрана будет стартовая вершина ). Выбранная таким образом вершина отмечается помеченной b[w] := true.

C этого момента значения и для помеченной вершины w не изменяются (см. основное утверждение далее).

Далее, на текущей итерации, из вершины производятся релаксации: просматриваются все непомеченные вершины , и для каждой такой вершины алгоритм пытается улучшить значение . Пусть длина дуги равна , тогда в виде кода релаксация выглядит как:

.

Здесь сравнивается

- длина найденного ранее кратчайшего пути до v без захода в w;

– длина кратчайшего пути с заходом в промежуточную вершину w (то есть длина кратчайшего пути до w плюс длина ребра от w до v)

При каждой успешной релаксации, т.е. когда c помощью промежуточной вершины происходит сокращение пути до некоторой вершины , в массив записывается, что предком вершины на этом пути является вершина :

p[v] := w.

На этом текущая итерация заканчивается, алгоритм переходит к следующей итерации (снова выбирается вершина с наименьшей величиной , из неё производятся релаксации, и т.д.). При этом в конце концов, после итераций, все вершины графа станут помеченными, и алгоритм свою работу завершает.

Заметим, что, если не все вершины графа достижимы из вершины , то значения для них так и останутся бесконечными. Понятно, что несколько последних итераций алгоритма будут как раз выбирать эти вершины, но никаких изменений эти итерации производить не будут (поскольку бесконечное расстояние не сможет прорелаксировать другие, даже тоже бесконечные расстояния). Поэтому работу алгоритма можно сразу останавливать, как только в качестве выбранной вершины берётся вершина с бесконечным расстоянием.

Восстановление путей Здесь используется тот факт, что если взять кратчайший путь до какой-то вершины , а затем удалить из этого пути последнюю вершину, то получится путь, оканчивающийся некоторой вершиной , и этот путь будет кратчайшим для вершины .

Кратчайший путь можно будет восстановить по массиву предков, каждый раз находя предка от текущей вершины, пока не придём в стартовую вершину — так получится искомый кратчайший путь, записанный в обратном порядке. Итак, кратчайший путь до вершины равен:

Основное утверждение, на котором основана корректность алгоритма Дейкстры, следующее. Утверждается, что после того как какая-либо вершина становится помеченной, текущее расстояние до неё уже является кратчайшим, и, соответственно, больше меняться не будет.

Доказательство будем производить по индукции. Для первой итерации справедливость его очевидна — для вершины имеем , что и является длиной кратчайшего пути до неё. Пусть теперь это утверждение выполнено для всех предыдущих итераций, т.е. всех уже помеченных вершин; докажем, что оно не нарушается после выполнения текущей итерации. Пусть — вершина, выбранная на текущей итерации, т.е. вершина, которую алгоритм собирается пометить. Докажем, что действительно равно длине кратчайшего пути до неё (обозначим эту длину через ).

Рассмотрим кратчайший путь до вершины . Этот путь можно разбить на два пути: , состоящий только из помеченных вершин (как минимум стартовая вершина будет в этом пути), и остальная часть пути (она тоже может включать помеченные вершины, но начинается обязательно с непомеченной). Обозначим через 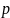первую вершину пути , а через — последнюю вершины пути .

Докажем сначала утверждение для вершины , т.е. докажем равенство . Это очевидно, так как на одной из предыдущих итераций была выбрана вершина и выполнялась релаксация из неё. Поскольку (в силу самого выбора вершины ) кратчайший путь до равен кратчайшему пути до плюс ребро , то при выполнении релаксации из величина действительно установится в требуемое значение.

Вследствие неотрицательности стоимостей рёбер длина кратчайшего пути (а она по только что доказанному равна ) не превосходит длины кратчайшего пути до вершины . Учитывая, что (ведь алгоритм Дейкстры не мог найти более короткого пути, чем это вообще возможно), в итоге получаем соотношения:

С другой стороны, поскольку и , и — вершины непомеченные, то так как на текущей итерации была выбрана именно вершина , а не вершина , то получаем другое неравенство:

Из этих двух неравенств заключаем равенство , а тогда из найденных до этого соотношений получаем что и требовалось доказать.

Реализация Время работы алгоритма складывается из:

• раз поиск вершины с наименьшей величиной среди всех непомеченных вершин, т.е. среди вершин из .

• раз производится попытка релаксаций

При простейшей реализации этих операций на поиск вершины будет затрачиваться операций, а на одну релаксацию — операций, и итоговая асимптотическая временная сложность алгоритма составляет .

Листинг 4.1.1. Реализация алгоритма Дейкстры:

procedure Diykstra(l: Matrix; var d, p:Vector); // l – матрица стоимости ребер

// d – вектор длин кратчайших путей

// p – вектор вершин пути

const

n = 6;

var

b:array[1..6]of boolean;//список просмотренных вершин

i, s, v, m, w: integer;

begin

(1) fillchar(b,sizeof(b),0); // отмечаем все вершины непомеченными

(2) fillchar(d,sizeof(d), 10000); // в качестве бесконечности примем

(3) fillchar(p,sizeof(p), 10000); // значение 1000, заполняем им векторы d и p

(4) s := 1; // устанавливаем источник

(5) d[s] := 0; //расстояние до начальной вершины

(6) p[s] := s; // предок источника равен самому себе

(7) for i:=1 to n do

begin

(8) m := 10000;

(9) for v := 1 to n do // выбор из множества V\S такой вершины w,

(10) if ( (d[v] <= m) and (not b[v]) ) then // что значение d[w] минимально

begin

(11) m:=d[v];

(12) w:=v;

end;

(13) b[w] := true; // Добавить w к множеству S

(14) for v := 1 to n do

(15) if ((not b[v]) and ((d[w]+l[w,v])<d[v])) then // релаксации: просмотр всех

begin // ребер (w,v),исходящих из вершины

(16) d[v] := d[w] + l[w,v]; // w, чтобы найти меньшее значение d[v]

(17) p[v] := w;

end;

end;

end;

Здесь граф хранится в виде матрицы стоимости ребер: для каждой вершины полагаем не принадлежит графу и .

После чтения заводятся массивы расстояний , меток и предков (строки (1)-(6)). Затем выполняются итераций. На каждой итерации сначала находится вершина , имеющая наименьшее расстояние среди непомеченных вершин (строки (9)-(12)). Если расстояние до выбранной вершины оказывается равным бесконечности, то алгоритм останавливается. Иначе вершина помечается как помеченная (строка (13)), и просматриваются все непомеченные вершины v, для каждой из них выполняются релаксации с помощью w, как промежуточной вершины (строки (14)-(17)). Если релаксация успешна (т.е. расстояние меняется), то пересчитывается расстояние и сохраняется предок (строки (16)-(17)).

После выполнения всех итераций в массиве оказываются длины кратчайших путей до всех вершин, а в массиве — предки всех вершин (кроме стартовой ).

Пример.

Пользуясь алгоритмом Дейкстры найти кратчайшие пути источника 1 до остальных узлов орграфа и их стоимости.

Решение.

Заметим, что для ориентированного графа алгоритм Дейкстры формулируется также, как и для неориентированного.

Запишем матрицу стоимости (весов) дуг:

№ итерации	S (помеченные узлы)	w	d[1]	p[1]	d[2]	p[2]	d[3]	p[3]	d[4]	p[4]	d[5]	p[5]		d[6]		p[6]
начало	∅	-	0	1
1	{1}	1	0	1	6	1	2	1
2	{1,3}	3			5	3	2	1	7	3	3	3
3	{1,3,5}	5			5	3			6	5	3	3		7		5
4	{1,3,5,2}	2			5	3			6	5			7		5
5	{1,3,5,2,4}	4							6	5			7		5
6	{1,3,5,2,4,6}	6											7		5

начало: (строки 1-6) отмечаем все узлы непомеченными (S=∅), заполняем и , в качестве источника выбираем первый узел, устанавливаем для него длину пути и в качестве предка сам узел 1.

итерация 1: (строки 9-12) наименьшая величина из невыбранных для узла

(строка 13) отмечаем , значения и далее не изменяются

(строка 14) просмотр непомеченных узлов , и попытки релаксации для них с помощью промежуточного узла ,

(строка 15) условие релаксации выполняется для узла 2: так как

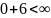
(строки 16-17) новые значения и соответственно 6 и 1

(строка 15) условие релаксации выполняется для узла 3: так как

(строки 16-17) новые значения и соответственно 2 и 1.

(строка 15) значения d[4], p[4], d[5], p[5], d[6], p[6] не изменяются, так как условие релаксации не выполняется для узлов 4,5,6.

итерация 2: наименьшая величина для непомеченных узлов: для узла .

(строка 13) Помечаем (заносим в S), значения и далее не изменяются

(строка 14) просмотр непомеченных узлов , и попытки релаксации для них с помощью промежуточного узла

(строка 15) условие релаксации выполняется для узла 2:

(строки 16-17) новые значения и соответственно 5 и 3

(строка 15) условие релаксации выполняется для узла 4: 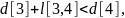так как

(строки 16-17) новые значения и соответственно 7 и 3

(строка 15) условие релаксации выполняется для узла 5: так как

(строки 16-17) новые значения и соответственно 3 и 3

(строка 15)значения d[6], p[6] не изменяются, так как условие релаксации не выполняется для узла 6.

итерация 3: наименьшая величина для непомеченных узлов: для узла

(строка 13) Помечаем (заносим в S), значения и далее не изменяются

(строка 14) просмотр непомеченных узлов , и попытки релаксации для них с помощью промежуточного узла ,

(строка 15) условие релаксации выполняется для узла 4: так как

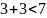
(строки 16-17) новые значения и соответственно 6 и 5

(строка 15) условие релаксации выполняется для узла 6: так как

(строки 16-17) новые значения и соответственно 7 и 5

(строка 15) значения d[2], p[2] не изменяются, так как условие релаксации не выполняется для узла 2.

итерация 4: наименьшая величина для непомеченных узлов: для узла

(строка 13) Помечаем (заносим в S), значения и далее не изменяются

(строка 14) просмотр непомеченных узлов , и попытки релаксации для них с помощью промежуточного узла ,

(строка 15) из непомеченных узлов 4 и 6 условие релаксации ни для одного не выполняется. Значения d[4], p[4], d[6], p[6] не изменяются

итерация 5: наименьшая величина для непомеченных узлов: для

(строка 13) Помечаем (заносим в S), значения и далее не изменяются

(строка 14) просмотр непомеченных узлов , и попытки релаксации для них с помощью промежуточного узла ,

(строка 15) для узла 6 условие релаксации не выполняется, значения d[6], p[6] не изменяются

итерация 6: наименьшая величина для непомеченных узлов: для узла

(строка 13) Помечаем (заносим в S), значения и далее не изменяются

все узлы отмечены, т. е. и не осталось узлов таких, что выполняется условие строки (15).

выход из цикла (7)-(17).

Результат

Стоимость кратчайшего пути до узла 2 ;

Востановим путь ; , таким образом путь:

Стоимость кратчайшего пути до узла 3 ;

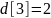Востановим путь , таким образом путь:

Стоимость кратчайшего пути до узла 4 ;

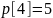Востановим путь , , таким образом путь:

Стоимость кратчайшего пути до узла 5 ;

Востановим путь , таким образом путь:

Стоимость кратчайшего пути до узла 6 ;

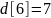Востановим путь , , таким образом путь:

60