14. Неравенство Чебышева.

Рассмотрим дискретную случайную величину Х, заданную таблицей распределения:

Х	X1	X2	…	Xn
P	P1	P2	…	Pn

Неравенство Чебышева.

Вероятность того, что отклонение случайной величины от её математического ожидания не превышает по абсолютной величине положительного числа не меньше, чем :

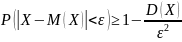
Доказательство: Так как события, состоящие в осуществлении неравенств и 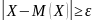противоположны, то сумма их вероятностей равна единице.

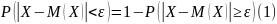
Напишем выражение дисперсии случайной величины Х:

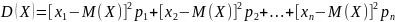
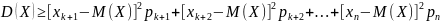
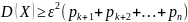
По теореме сложения сумма вероятностей 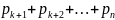есть вероятность того, что Х примет одно, безразлично какое, из значений , а при любом из них отклонение будет удовлетворять неравенству . Отсюда следует, что сумма выражает вероятность 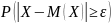. Значит:

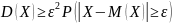
Подставляя (3) в (1), окончательно получим что и требовалось доказать.

15. Теорема Чебышева.

Теорема Чебышева: При достаточно большом числе независимых опытов среднее арифметическое наблюдённых значений случайной величины сходится по вероятности к её математическому ожиданию.

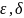- произвольно малые положительные числа

Аналогично этому, по теореме Чебышева, при увеличении n среднее арифметическое 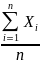сходится по вероятности к 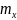, то есть:

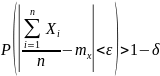
Доказательство:

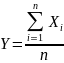
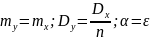
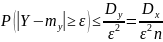
Как бы мало не было число Ɛ, можно взять n таким большим, чтобы выполнялось неравенство: . Тогда:

Что и требовалось доказать.

16. Обобщенная теорема Чебышева. Теорема Маркова.

Обобщенная теорема Чебышева.

Если 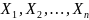- независимые случайные величины с математическими ожиданиями 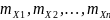и дисперсиями и если все дисперсии ограничены сверху одним и тем же числом L: 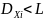, то при возрастании L среднее арифметическое наблюденных значений сходится по вероятности к среднему арифметическому их математических ожиданий.

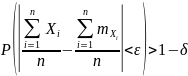
Доказательство: Математическое ожидание величины равно 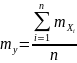, а дисперсия 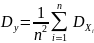. Применим неравенство Чебышева:

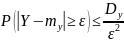
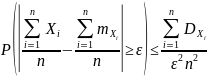
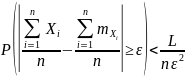
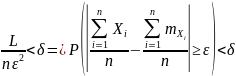
Откуда, переходя к противоположному событию, получим доказываемое неравенство.

Теорема Маркова.

Если имеются зависимые случайные величины и при n  ∞

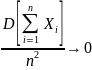, то среднее арифметическое наблюденных значений величин сходится по вероятности к среднему арифметическому их математических ожиданий.

Доказательство: Рассмотрим величину . Очевидно, 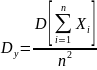. Применим неравенство Чебышева:

Так как n  ∞ , то при достаточно большом n 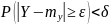. Переходя к противоположному событию, получим:

Что и требовалось доказать.

17. Характеристические функции.

Характеристической функцией случайной величины Х называется функция

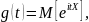
Где i – мнимая единица. Функция g(t) представляет собой математическое ожидание некоторой комплексной случайной величины 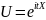, функционально связанной с величиной Х.

Зададим Х – дискретную случайную величину её рядом распределения

Xi	X1	X2	…	Xn
Pi	P1	P2	…	Pn

То её характеристическая функция .

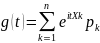Если Х – непрерывная случайная величина с плотностью распределения f(x), то .

Обратное преобразование Фурье:

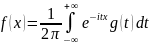
Свойства характеристических функций:

1. Если случайные величины X и Y связаны соотношением , где а – неслучайный множитель, то их характеристические функции связаны соотношением:

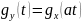
Доказательство:

2. Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых.