Додаткові завдання по модулю № 1

№ 1 Дані дві точки А(3;-4;-2) і В(2;5;-1). Знайти проекцію вектора на вісь, яка складає з координатними осями Ox та Oy кути , , а з віссю Oz – тупий кут .

№2. В тетраедрі OABC точки K, L, M, N, P, Q - середини ребер OA, OB, OC, AB, AC, BC відповідно, S – точка перетину мередіан трикутника ABC. Приймаючи за базисні вектори знайти у цьому базисі кординати:

1. Векторів

2. векторів ;

3. векторів .

№3. У трикутнику ABC проведена бісектриса AD. Знайти координати вектора у базисі, утвореного векторами .

№4. Довести, що радіус–вектор центру правильного багатокутника є середнє арифметичне радіус-векторів його вершин.

№5. Знаючи радіус–вектори r₁, r₂, r₃ трикутника знайти радіус–вектор центра кола, вписаного у трикутник.

№6. Однорідний дріт зігнутий у вигляді кута AOB зі сторонами = a, =b. Знайти координати центру тяжіння дроту в системі координат O, , .

№7. Точки K і L є серединами сторін AB і BC паралелограма OABC. Довести, що точка перетину діагоналей OABC співпадає з точкою перетину медіан трикутника OKL.

№8. На сторонах AB, BC і CA трикутника ABC взяті відповідні точки M, N, P так, що , , . Площа трикутника ABC дорівнює S . Знайти площу трикутника отриманого при перетині прямих AN, BP і CM. Вивести звідси, що медіани трикутника перетинаються в одній точці.

№9. Довести, що чотири відрізка, що сполучають вершини тетраедра з точками перетину медіан протилежних граней, перетинаються в одній точці і діляться у цій точці у співвідношенні 3:1.

№10. Дані три вектора: a(-1,-1,1), b(5,1,1), c(0,3,-2)

Обчислити

1. b (a, c) - c (a, b); 2) + - (a, b)(b, c); 3) (a, c)(a, b) + (b, c);

№11. З однієї точки відкладені три вектори a(0,-3, 4), b(4,1,-8) і c. Вектор c має довжину 1 і ділить навпіл кут між a і b. Обчислити координати вектора c.

№12. Знайти суму ортогональних проекцій вектора a на сторони правильного трикутника.

№13. У рівнобедреному трикутнику медіани проведені до бічних сторін взаємно перпендикулярні. Знайти кути трикутника.

№14. Дані α,β,γ плоскі кути тригранного кута. Знайти його двогранні кути.

№15. Дві трійки векторів a₁, a₂, a₃ та b₁, b₂, b₃ називаються взаємними, якщо (a_i,b_j)=δ_ij. Для трійки векторів a₁(3,0,1) , a₂(-1,1,2), a₃(1,2,1) знайти взаємну трійку.

№16. Довести, що площа трикутника, складеного із медіан трикутника ABC, рівна ¾ площі трикутника ABC.

№17. В просторі дано дві прямокутні системи координат 0, e₁, e₂, e₃ та 0’, e’₁, e’₂, e’₃. Початок другої системи координат має в першій наступні координати -1, 3, 5. Вектор e’₁ утворює кути 60° з векторами e₁ та e₂, та гострий кут з вектором e₃. Вектор e’₂ комланарний з векторами e₁ та e₂, та утворює гострий кут з вектором e₂. Трійки e₁, e₂, e₃ та e’₁, e’₂, e’₃ однаково орієнтовані. Знайти координати точки простору в першій СК, якщо відомі її координати в другій СК.

Матриці, ввизначники,слар

№ 1. Нехай x = r cos φ cos ψ, y = r sin φ cos ψ, z = r sin ψ.

Обрахуйте якобіан

№ 2. Нехай в матриці А порядку n точно n елементів дорівнюють 1, а інші – нулі. Чому може дорівнювати визначник матриці А ?

№ 3. Як зміниться визначник, якщо всі елементи матриці замінити комплексно спряженими числами ?

№ 4. Обрахувати визначники порядку n (корисно отримати рекурентну формулу) :

№ 5. Показати, що визначник матриці А порядку n дорівнює 0, якщо в ній є нульова підматриця розмірів

k l, і k+ l > n.

№ 6. Числа 1081, 1403, 2093 і 1541 діляться на 23. Поясніть без обрахування, чому число

також ділиться на 23.

№ 7. Довести, що det ( A – λE ) – многочлен від λ, і обрахувати його коефіцієнти.

№ 8. Доведіть, що для будь-якої дійсної матриці А виконано det AA^T ≥ 0.

№ 9. Обрахуйте:

1) 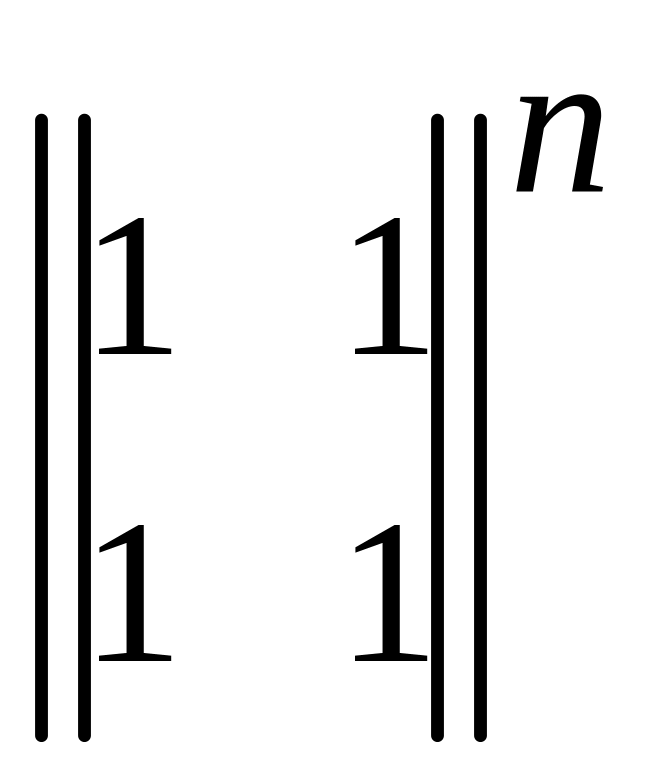; 2) ; 3)

№ 10. Обрахуйте f (A), якщо:

1. f (t) = t² - 2t + 1, A = ;

2. f (t) = t² - 2t + 1, A = ;

№ 11. На яку матрицю необхідно помножити матрицю А , щоб в результаті отримати:

1) перший стовпчик А ; 2) першу стрічку А?

№ 12. Нехай А – вироджена матриця другого порядку, m - натуральне число. Довести, що існує число λ таке, що А^m = λ^m-1 A для всіх m.

№ 13. Обрахувати:

1) 2) 3)

№ 14. Обрахувати:

№ 15. Нехай А² + А + Е = 0. Довести, що матриця А невироджена і вказати найпростіший спосіб обрахування А^-1

№ 16. Нехай А^m = 0. Довести, що (Е - А)^-1 = Е + А + ... + А^{m - 1}

№ 17. Нехай матриці А, С невироджені. Розв’язати матричне рівняння:

1) АХ = 0; 2) АХ = В; 3) ХА = В; 4) АХС = В;

5) А (Х+С) = В.

№ 18. 1) Знайти загальний вигляд ермітових матриць другого порядку.

2) Знайти загальний вигляд косоермітових матриць другого порядку.

3) Вказати всі матриці перестановок другого порядку.

№ 19. Довести твердження: Дійсна унітарна матриця ортогональна.

№ 20. Довести твердження: Якщо матриці А і В ортогональні, то АВ ортогональна.

№ 21. Довести, що не існує матриць А і В таких,

що АВ – ВА = Е.

№ 22. Обрахувати визначник Вандермонда:

№ 23. Вказати який-небудь базисний мінор і визначити ранг матриці:

1) ; 2) ; 3) .

№ 24. Довести, що якщо стовпчики матриці В є лінійними комбінаціями стовпчиків матриці А, то rg B ≤ rg A.

№ 25. 1). Оцінити ранг добутку двух матриць через ранги співмножників.

2). Навести приклади, коли виконані співвідношення:

rg AB < rg A, rg AB< rg B, rg AB < min (rg A, rg B),

rg AB = rg A, rg AB = rg B.

№ 26. Матриці А і В мають розміри m×r і r×n відповідно, і rg AB = r. Знайти ранги матриць А і В.

№ 27. Довести, що будь-яку матрицю рангу r можна представити у вигляді суми r матриць рангу 1.

№ 28. Нехай матриці А і В мають розміри відповідно m×n і n×p, і нехай АВ = 0. Довести, що rg A + rg B ≤ n.

№ 29. Виписати розширену матрицю даної системи рівнянь. Розв”язати систему

х₁ + х₂ = 3,

х₁ + х₃ = 4,

х₁ + х₄ = -2,

х₁ + х₅ = -1,

х₁ + х₆ = 0,

х₂ +х₃ + х₄ + х₅ +х₆ = -1.

№ 30. Виписати матрицю коефіцієнтів даної системи лінійних однорідних рівнянь. Розв”язати систему.

2x₁ + 4x₂ + 6x₃ + x₄ = 0

x₁ + 2x₂ + 3x₃ + x₄ = 0

3x₁ + 6x₂ + 9x₃ - x₄ = 0

x₁ + 2x₂ + 3x₃ + 5x₄ = 0

№ 31. Розв”язати систему лінійних рівнянь :

6x₁ + 3x₂ + 14x₃ – 2x₄ + x₅ = 2

20x₁ + 5x₂ + 10x₃ + 4x₄ + 11x₅ = 20

13x₁ + 4x₂ + 12x₃ + x₄ + 6x₅ = 11

4x₁ + 7x₂ + 46x₃ – 12x₄ - 7x₅ = -12

x₁ - 2x₂ - 16x₃ + 5x₄ + 4x₅ = 7

№ 32. Сформулювати необхідну і достатню умову того, що система m лінійних рівнянь з n невідомими має єдиний розв’язок.

№ 33. Довести, що якщо стовпчики основної матриці лінійно незалежні, то система лінійних рівнянь має не більше одного розв’язку.

№ 34. Довести, що якщо стрічки основної матриці лінійно незалежні, то система рівнянь сумісна при будь-якому стовпчику вільних членів.

№ 35. 1) Сформулювати в термінах рангів і довести умову на декартові координати (а₁, b₁), (a₂, b₂), (a₃, b₃) трьох точок площини, необхідну і достатню для того, щоб ці точки не лежали на одній прямій.