
- •1. Решение систем линейных уравнений методом Гаусса
- •2. Матрицы. Равенство матриц. Операции над матрицами: транспонирование, сложение, умножение на число, произведение матриц
- •3. Определители 2-ого и 3-его порядков: их определения и свойства
- •4. Обратная матрица: определение, необходимое и достаточное условие ее существования. Нахождение обратной матрицы для квадратных матриц второго и третьего порядков
- •5. Правило Крамера для решения систем линейных уравнений
- •6. Решение системы линейных уравнений с помощью обратной матрицы
- •7. Определение свободного вектора
- •8. Сложение векторов и умножение их на число
- •9. Базис пространства векторов. Координаты вектора в базисе
- •10. Скалярное произведение и его свойства
- •11. Ортонормированный базис. Скалярное произведение в ортонормированном базисе. Длина вектора, угол между векторами.
- •12. Прямоугольная система координат в пространстве и на плоскости. Расстояние между двумя точками
- •13. Различные формы уравнения прямой на плоскости
- •14. Взаимное расположение двух прямых. Нахождение точки пересечения, угла между прямыми. Условия параллельности и перпендикулярности прямых
- •15. Вывод канонического уравнения окружности
- •16. Эллипс: определение, каноническое уравнение, свойства
- •17. Гипербола: определение, каноническое уравнение, свойства
- •18. Парабола: определение, каноническое уравнение, свойства
- •19. Плоскость
- •20. Вывод канонического уравнения сферы. Шар. Эллипсоид
- •21. Определение линейного пространства строк
- •22. Линейная независимость и линейная зависимость векторов: определения, примеры
- •23. Базис линейного пространства, его свойства. Координаты вектора в базисе
- •24. Ранг матрицы и методы его нахождения
- •25. Евклидово пространство. Скалярное произведение и его свойства
- •26. Ортонормированный базис
- •27. Определения отображения и линейного преобразования. Примеры
- •28. Матрица линейного преобразования
- •29. Собственные векторы матрицы: определение, метод нахождения
25. Евклидово пространство. Скалярное произведение и его свойства
Евклидово пространство – это линейное пространство со скалярным произведением.
Определение
Пусть
- стандартный базис
("бегущая единица"). Пусть
![]() .
Тогда
.
Тогда
![]()
![]()
Скалярным произведением называется число
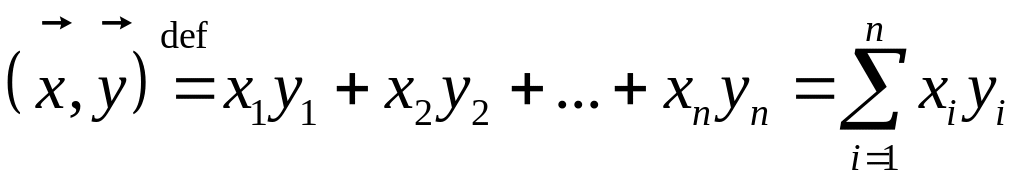 (*)
(*)
Свойства
1.
![]()
2.
![]() (доказательство:
(доказательство:
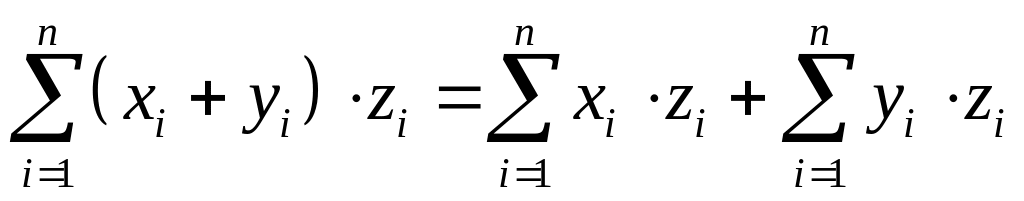 )
)
3.
![]()
![]()
4.
![]() ,
,
![]()
Что дает скалярное произведение?
I.
Длина
![]() вектора
:
вектора
:
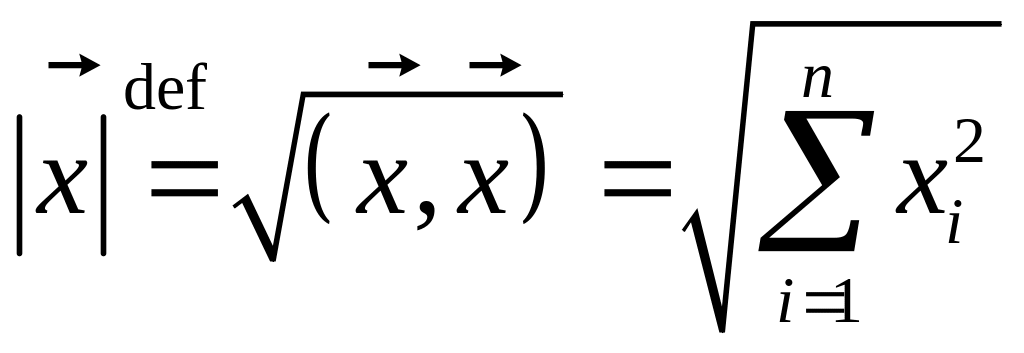
Свойства
1.
![]() ,
,
![]()
2.
![]()
3. Нормирование
вектора
![]() :
:
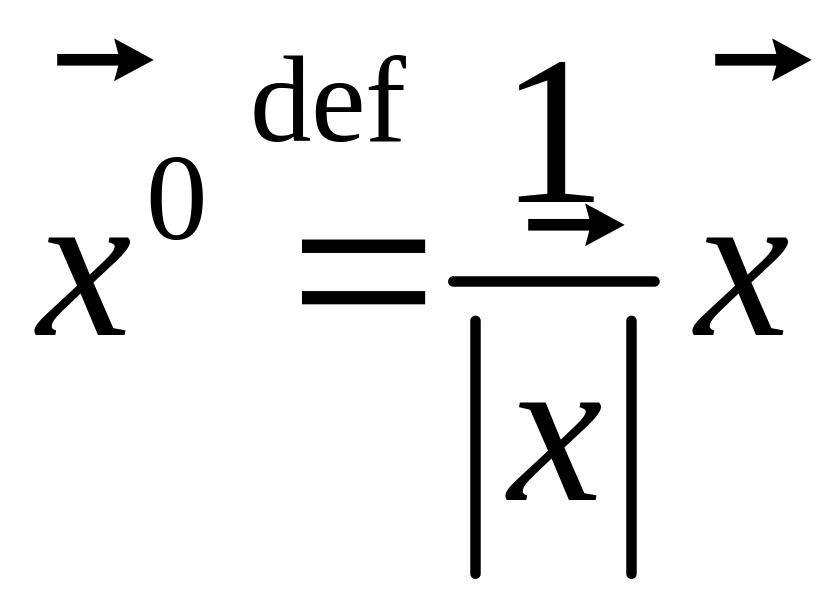 ,
,
![]() .
.
II. Неравенство Коши-Буняковского
Для
![]()
![]() ,
причем
,
причем
![]() и
и
![]() коллинеарны (
коллинеарны (![]() или
или
![]() )
)
Следствие
1.
![]() - неравенство треугольника
- неравенство треугольника
2. При
![]()
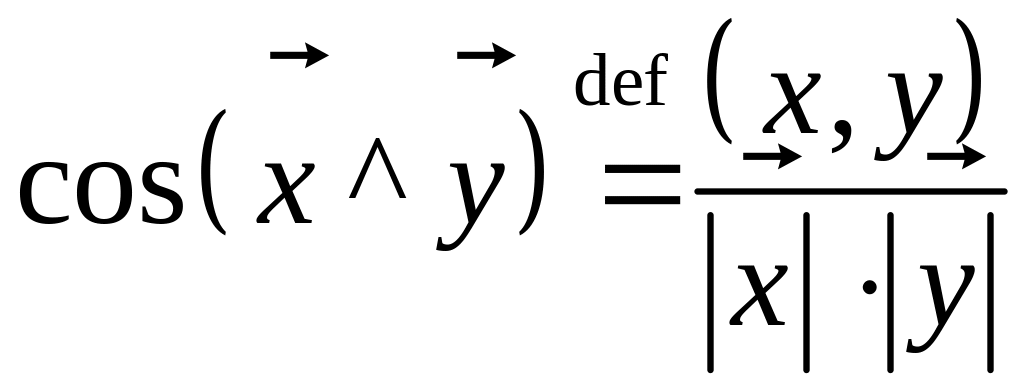 (1)
(1)
Из (1)
![]()
[_]
26. Ортонормированный базис
Определение
Пусть
.
и
называются ортогональными
(![]() )
)
![]() (
(![]() )
)
Определение
Система называется ортонормированной, если она состоит из попарно перпендикулярных векторов длины 1.
![]() при
при
![]() и
и
![]() или
или
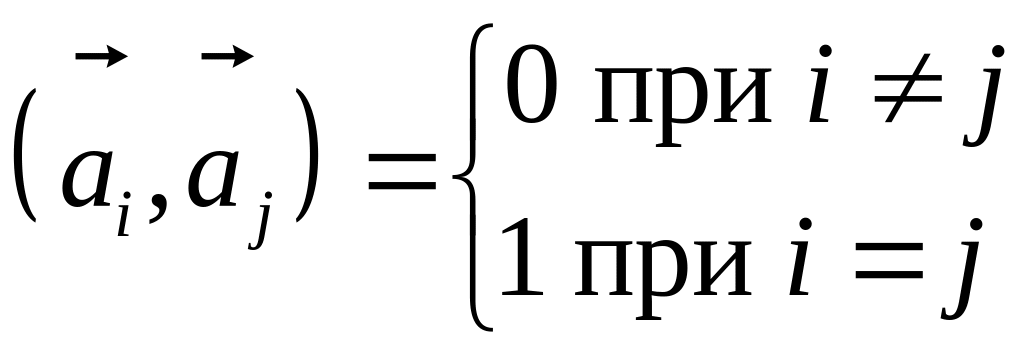
Теорема
Любая ортогональная
система
![]() в
линейно независима.
в
линейно независима.
Доказательство
Пусть
![]() (*)
(*)
Умножим (*) скалярно
на
![]() :
:

![]()
Аналогично, умножив
(*) на
![]() ,
получим
,
получим
![]() и т.д. Получили, что
.
и т.д. Получили, что
.
Следствие
Ортонормированная система из векторов является ортонормированным базисом .
Теорема
Пусть - ортонормированный базис в .
![]() ,
,
![]()
Тогда
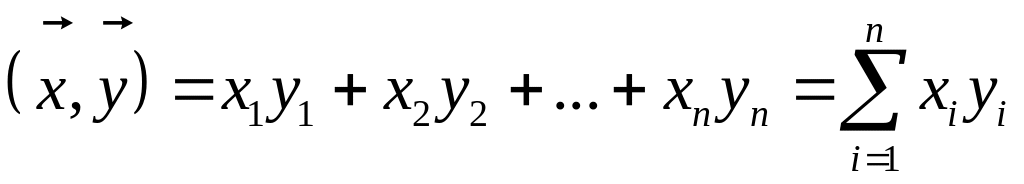 [_]
[_]
27. Определения отображения и линейного преобразования. Примеры
Определение
Пусть
![]() - множества (возможно
- множества (возможно
![]() ).
Отображение
).
Отображение
![]() это закон, по которому каждому элементу
это закон, по которому каждому элементу
![]() ставится в соответствие единственный
элемент
ставится в соответствие единственный
элемент
![]() .
Обозначается
.
Обозначается
![]() .
.
Пример
Числовая функция
![]() с областью определения
с областью определения
![]() - это отображение
- это отображение
![]() .
.
Определение
Пусть
- линейное (евклидово) пространство.
Отображение
![]() называется линейным
преобразованием,
если для
называется линейным
преобразованием,
если для
![]() и
и
1.
![]()
2.
![]()
Следствия
![]() (док-во:
(док-во:
![]() )
)
![]()
Пример
Числовая функция
![]() является линейным преобразованием:
является линейным преобразованием:
1.
![]()
2.
![]()
[_]
28. Матрица линейного преобразования
Пусть
:
- базис в
.
Пусть
![]()
![]()
Будем обозначать
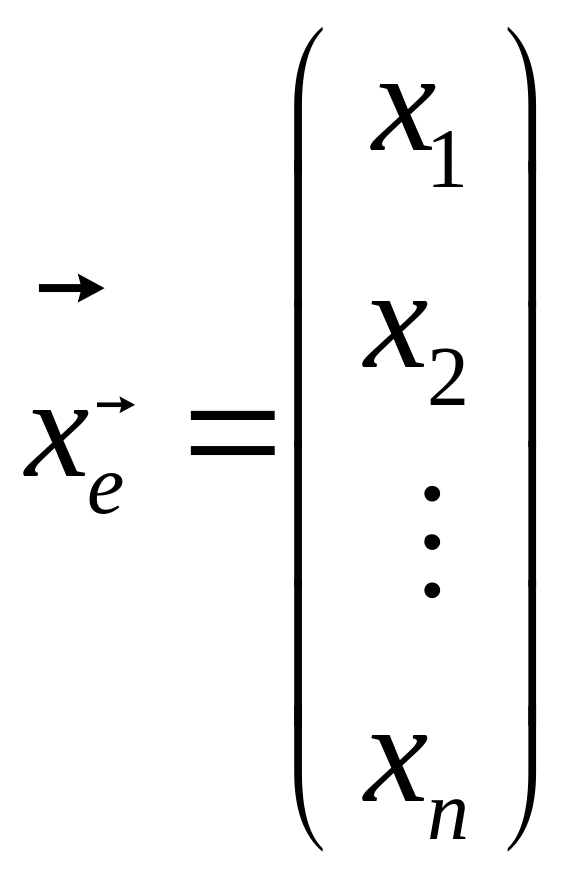
Пусть для каждого
![]()
![]() разложение
разложение
![]() по
:
по
:
![]()
Матрицей линейного преобразования называется матрица
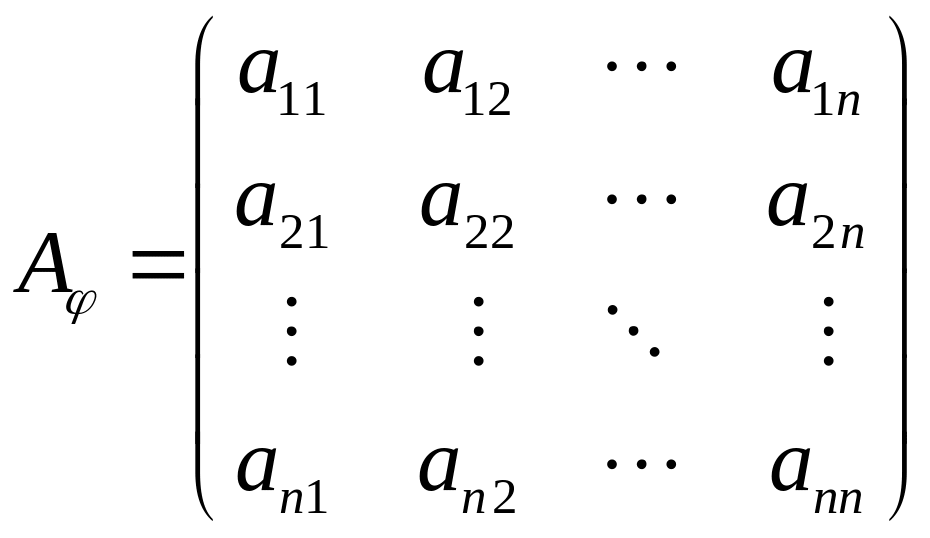 ,
,
т.е. матрица, по столбцам которой записаны координаты в базисе .
Доказывается, что
для
![]()
![]()
[_]
29. Собственные векторы матрицы: определение, метод нахождения
Пусть
- квадратная матрица
,
.
Пусть
![]() - записанный в столбец вектор
.
Тогда
- записанный в столбец вектор
.
Тогда
![]() имеет размерность
имеет размерность
![]() - то есть это тоже вектор из
.
- то есть это тоже вектор из
.
Определение
Вектор
![]() из
называется собственным
вектором
(СВ) квадратной матрицы
порядка
,
если
из
называется собственным
вектором
(СВ) квадратной матрицы
порядка
,
если
![]() ,
,
где
- некоторое число, называемое собственным
значением (СЗ) СВ
![]() .
.
Почему СВ ?
![]() для любого
,
для любого
,
т.е. был бы СВ с любым СЗ .
Метод нахождения
Пусть
- квадратная матрица порядка 3. Ищем СВ
в виде
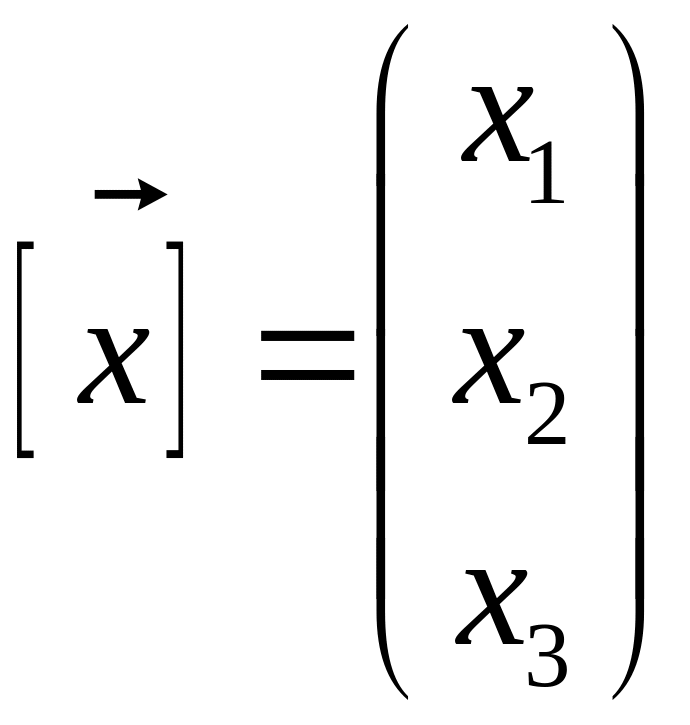 ,
где
,
где
![]() - неизвестные и
,
так как это СВ.
- неизвестные и
,
так как это СВ.
![]()
![]()
![]()
![]()
Можно записать
![]()
Таким образом, мы получили матричный вид однородной СЛУ с неизвестными :
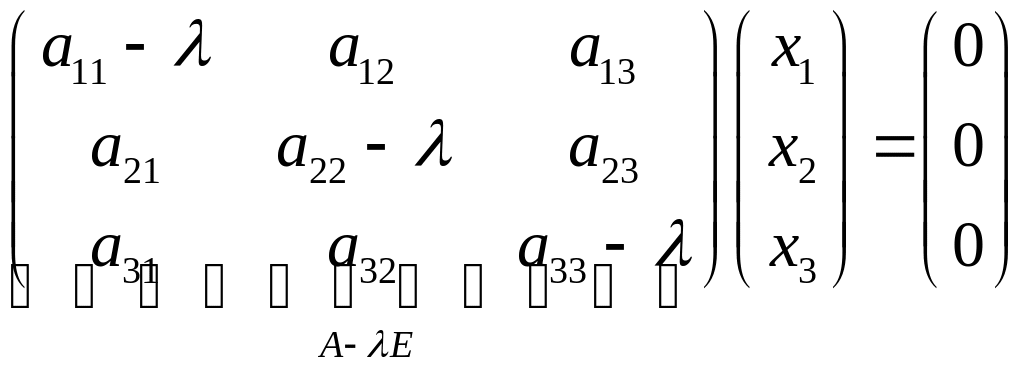 (*)
(*)
Очевидно, что вектор
![]() является решением этой системы. По
правилу Крамера, если
является решением этой системы. По
правилу Крамера, если
![]() ,
то система имеет единственное решение
– вектор
,
но по определению
не может быть СВ. Значит для нахождения
СВ необходимо, чтобы
,
то система имеет единственное решение
– вектор
,
но по определению
не может быть СВ. Значит для нахождения
СВ необходимо, чтобы
![]()
Определение
Пусть - квадратная матрица . Тогда
![]()
Называется характеристическим многочленом матрицы . Степень этого многочлена .
СВ матрицы существуют только для тех , которые являются корнями характеристического многочлена этой матрицы. Поэтому
1. Находим характеристический многочлен матрицы
![]()
и его корни
![]() - СЗ матрицы
.
- СЗ матрицы
.
2. Подставляем в (*)
![]() .
Общее решение этой СЛУ – множество всех
СВ для СЗ
.
Общее решение этой СЛУ – множество всех
СВ для СЗ
![]() .
.
3. Берем
![]() и т.д.
и т.д.
[_]
