19. Плоскость

Определение

Плоскость определяется точкой и нормальным вектором (т.е. ).

Нормальный вектор плоскости - любой ненулевой вектор перпендикулярный любому вектору, лежащему в плоскости .

Вывод уравнения плоскости в Декартовой системе координат

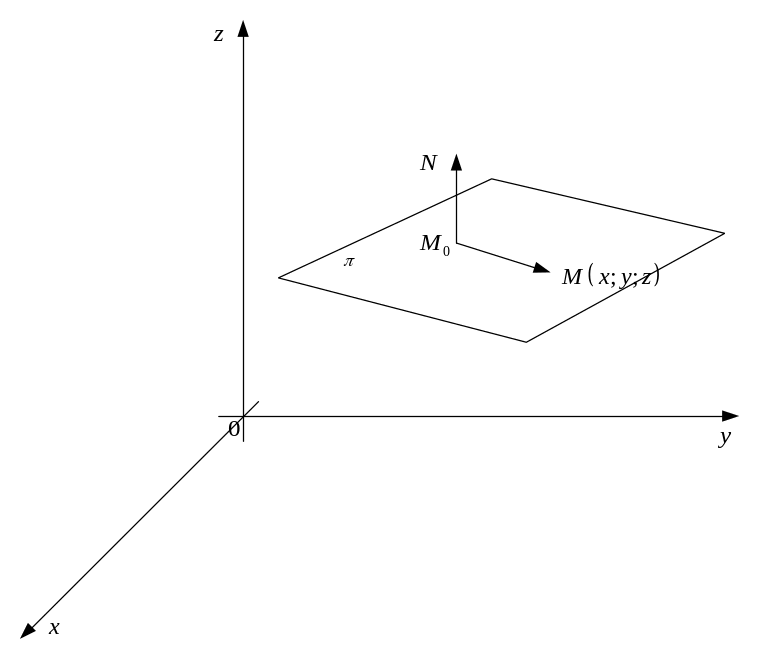
Точка .

Но , . Значит

(*)

Получили уравнение плоскости с нормальным вектором , проходящей через точку .

Преобразуем (*):

(**)

Получили каноническое уравнение плоскости.

Неполное уравнение плоскости

Рассмотрим (**)

1. начало координат (точка ) принадлежит плоскости

2. , т.к. , значит плоскость параллельна

3. , значит плоскость параллельна

4. , значит плоскость параллельна

Угол между плоскостями

Углом между плоскостями называется угол между их нормальными векторами:

Таким образом:

1. Плоскости параллельны, если их нормальные векторы колинеарны.

2. Плоскости перпендикулярны, если их нормальные векторы ортогональны.

[_]

20. Вывод канонического уравнения сферы. Шар. Эллипсоид

Сфера

Сфера – поверхность, каждая точка которой равноудалена от некоторой фиксированной точки (центра сферы) на положительное расстояние (радиус сферы).

Вывод канонического уравнения сферы радиуса с центром

сфере

Шар

Шар радиуса с центром в :

шару

Эллипсоид

Эллипсоид – поверхность с каноническим уравнением

[_]

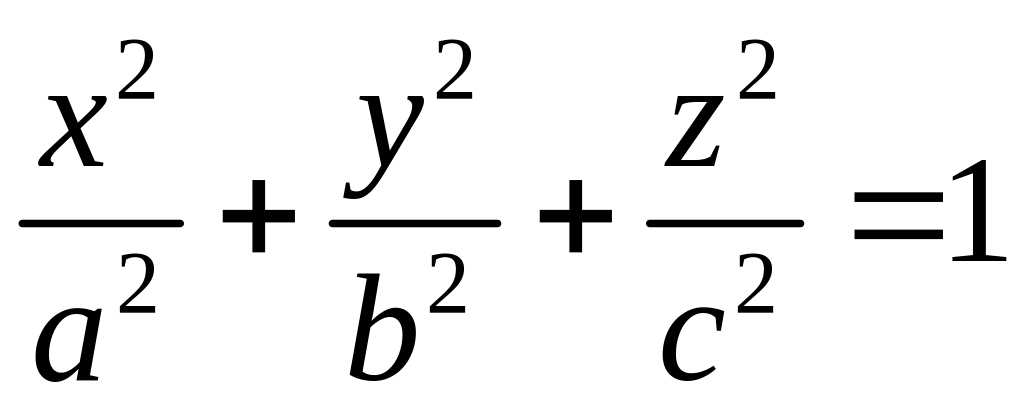
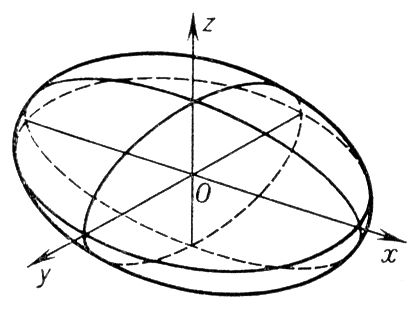
21. Определение линейного пространства строк

Пусть - натуральное фиксированное число.

- множество строк длины

Операции на

Сложение:

Умножение на :

Определение. с операциями сложения и умножения на число называется линейным пространством строк длины . Элементы называются -мерными векторами.

Вектор называется нулевым вектором.

[_]

22. Линейная независимость и линейная зависимость векторов: определения, примеры

Определение

Система векторов ( ) называется линейно независимой, если из равенства следует, что и линейно зависимой, если , не все равные нулю, такие что .

Следствие

Если к линейно зависимой системе добавить какие-то векторы , то полученная система останется линейно зависимой. Действительно, , не все равные нулю, но

Тогда . Значит - линейно зависимая система.

Лемма

- линейно зависимая система векторов тогда и только тогда, когда хотя бы один из векторов этой системы равен линейной комбинации остальных векторов.

Доказательство

Векторы линейно зависимы , не все равные нулю :

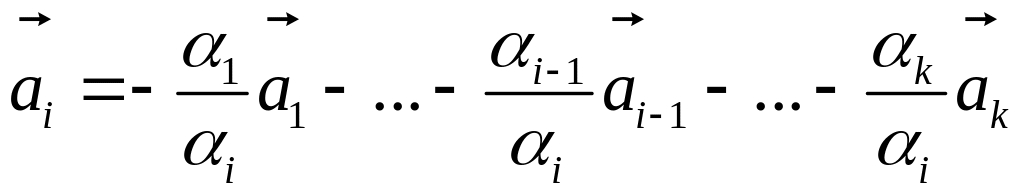
Пусть

Тогда

Значит - линейно зависимы.

Теорема

В векторы

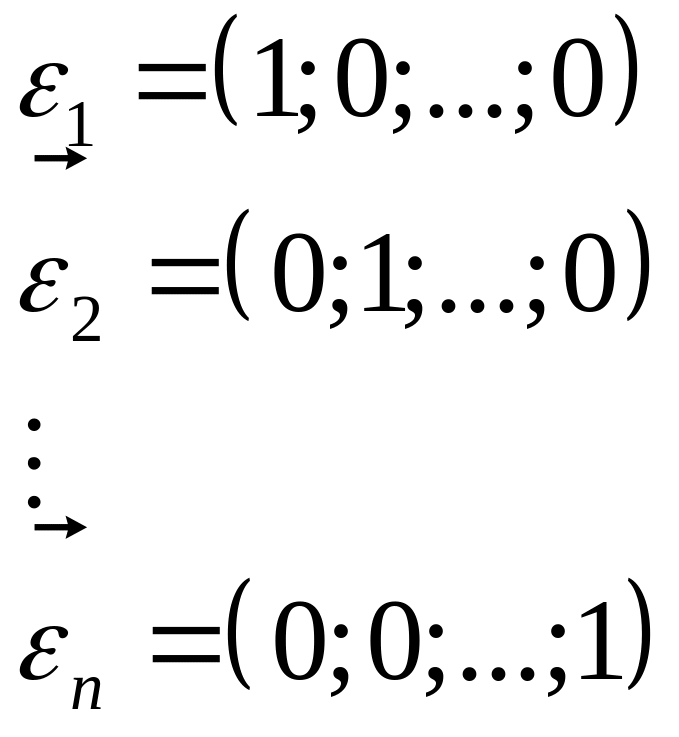
("бегущая единица") линейно независимы.

Доказательство

Пусть

Пример. Частные случаи линейной зависимости системы векторов в .

. По лемме образуют линейно зависимую систему хотя бы один из них линейно выражается через другой вектор или - коллинеарные вектора. Следовательно, два вектора линейно независимы они неколлинеарны.

. По лемме линейно зависимы хотя бы один из них линейно выражается через остальные векторы например, - компланарные векторы. Следовательно, 3 вектора линейно независимы они некомпланарны. В частности, некомпланарны - линейно независимые векторы.

. Любые 4 вектора линейно зависимы. Действительно, если компланарные, то они линейно зависимы и, следовательно, линейно зависимы. Если не компланарные, то равен их линейной комбинации (см. билет №9) и, следовательно, линейно зависимы.

[_]