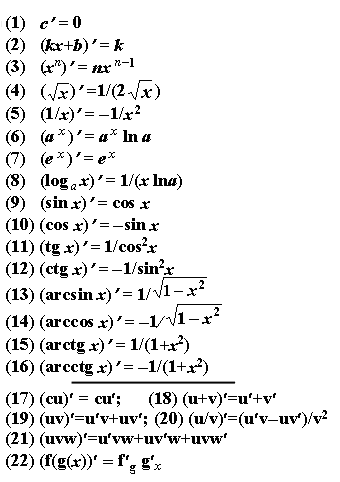Предел числовой последовательности.Примеры.

Последовательность - это функция, заданная на множестве натуральных чисел . Число называется пределом последовательности , если для любого положительного числа , как бы мало оно ни было, существует такой номер , что для всех c номерами справедливо неравенство . Неравенство , эквивалентное неравенству , означает, что для любого существует такой номер , что все c номерами расположены между и . Последовательность, предел которой - конечное число , называется сходящейся, и ее предел обозначают .

Единственность.предел суммы,произведения,частного.

теорема о единственности предела: ф-ия f(х) не может иметь более одного предела в точке х₀ (если предел ф-ии существует только один).

Теорема о пределе суммы, разности, произведения и частного двух функций

Если две последовательности {x_n} и {y_n} имеют пределы, равные соответственно a и b, то:

Суммы и разности;

     а) Последовательность {x_n y_n} имеет предел равный a b, т. е.

     Это свойство распространяется на случай любого фиксированнго числа слагаемых.

 

б) Последовательность {x_n y_n} имеет предел равный ab, т. е.

     Это свойство распространяется также на случай любого фиксированного числа сомножителей.

     Постоянный множитель можно выносить за знак предела при любом постоянном k.

     с) Последовательность имеет предел равный , т. е.

при условии, что все y_n не равны нулю и .

Предельный переход в неравенствах для последовательности.

     Теорема. Если элементы сходящейся последовательности {x_n}, начиная с некоторого номера, удовлетворяют неравенству x_n ≥ b (x_n ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).

     Теорема. Пусть {x_n} и {z_n} - сходящиеся последовательности, имеющие общий предел a. Пусть, кроме того, начиная с некоторого номера, элементы последовательности {y_n} удовлетворяют неравенствам x_n ≤ y_n ≤ z_n. Тогда последовательность {y_n} сходится и имеет предел a.

Теорема Вейерштрасса о пределе монотонной последовательности

Теорема Вейерштрасса Всякая монотонная и ограниченная последовательность имеет предел (эта теорема даётся в средней школе без доказательства). 

Монотонные последовательности: Для числовой последовательности справедливы все теоремы о пределах ф-ии.

1){Xn}-ограничена сверху если  М: Хn<=M n>=N

2){Xn}-ограничена снизу если  М: Хn>=M n>=N

3) {Xn}-ограниченная если она ограничена и сверху и снизу

 m, M; m<=Xn<=M n>=N

{Xn} если Хn+1>=Xn nN

{Xn} если Хn+1<=Xn nN

Если эти неравенства строгие то последовательность – строго убывающая или возрастающая. Возрастающие и убывающие последовательности называются монотонными.

Теорема о пределе монотонной последовательности: 1) если последовательность возрастает и ограничена сверху, то она имеет предел 2) если последовательность убывает и ограничена снизу, то она имеет предел  всякая монотонная ограниченная последовательность имеет предел.

Число “е”.

Число (число Эйлера, число Непера)

e — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e»

Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики.

Теорема об извлечении сходящейся подпоследовательности из огограниченной последовательности.

Т е о р е м а  1. Из всякой последовательности действительных чисел  можно выделить подпоследовательность , сходящуюся к конечному числу, или к , или к .

В случае, когда последовательность  не ограничена сверху (снизу), она, очевидно, содержит в себе подпоследовательность, стремящуюся к  (к ), что доказывает теорему. Если же последовательность ограничена, то теорема 1 сводится к следующей теореме.

Т е о р е м а  2 (Больцано-Вейерштрасса). Из всякой ограниченной последовательности  можно выделить подпоследовательность , сходящуюся к некоторому числу.

Определение предела функции в точке.

Пусть функция f(x) определена на множестве X = {x}, имеющем точку сгущения a. Запись

              (1)

обозначает, что для каждого числа ε > 0 существует число δ = δ(ε) > 0 такое, что для всех x, для которых f(x) имеет смысл и которые удовлетворяют условию 0 <|x - a|< δ, справедливо неравенство

|f(x) – A| < ε.

Для существования предела функции (1) необходимо и достаточно, чтобы для каждой последовательности x_n → a, x_n ≠ a (x_n є X; n = 1, 2, …), было выполнено равенство

.

Имеют место два замечательных предела:

1) ,           2)    

Эквивалентность определений по Коши и Гейне

Определение предела функции по Коши: пусть f(x) определена на множестве X, и a - предельная точка X. Число b называется пределом f(x) при x → a, если ∀ ε > 0 ∃ δ > 0 такое, что ∀ x ∈ {0 < x - a< δ}: f(x) - b < ε.

Определение предела функции в точке a по Гейне:

b называется пределом f(x) при x → a, если ∀ {x_n} → a (x_n ≠ a): {f(x_n)} → b.

Определения предела функции в точке a по Гейне и по Коши эквивалентны.

Свойства пределов функции

1) Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

Аналогично предел разности двух функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

5) Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

Первый и второй замечательные пределы

Первый замечательный предел

Второй замечательный предел

или

Эквивалентные бесконечно малые функции.Таблица эквивалентных бесконечно малых.

Функция α (x) называется бесконечно малой при , если

Предположим, что α (x) и β (x) - бесконечно малые функции при .

• Если , то говорят, что функция α (x) является бесконечно малой высшего порядка по сравнению с функцией β (x);

• Если , то говорят, что функции α (x) и β (x) являются бесконечно малыми одинакового порядка малости;

• Если , то говорят, что функция α (x) является бесконечно малой порядка n относительно функции β (x);

• Если 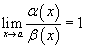, то говорят, что бесконечно малые функции α (x) и β (x) эквивалентны при .

Таблица эквивалентных бесконечно малых!

При вычислении предела отношения двух бесконечно малых функций мы можем заменить эти функции их эквивалентными выражениями.

Понятие непрерывности функции в точке

Пусть функция f (x) определена в некоторой окрестности точки х₀. Функция f (x) называется непрерывной в точке х₀, если предел функции и ее значение в этой точке равны, т. е.

для непрерывной функции можно переставить знак функции и знак предела. Если функция непрерывна в точке х₀, то она определенна в этой точке, т.е. существует f (x₀)

Непрерывность основных элементарных функций

все основные элементарные функции непрерывны при всех значениях х, для которых они определены. Как известно, элементарной называется такая функция, которую можно задать одной формулой, содержащей конечное число арифметических действий и суперпозиций (операции взятия функции от функции) основных элементарных функций. всякая элементарная функция непрерывна в каждой точке, в которой она определена.

Теорема Больцано-Коши о промежуточном значении

Непрерывная функция переменного x, положительная при некото-

ром значении x и отрицательная при некотором другом значении x из

замкнутого интервала непрерывности a 6 x 6 b, должна обращаться

в нуль при некотором промежуточном значении x. Итак, если функ-

ция f(x) непрерывна при изменении x от a до b, и при этом f(a) < 0

и f(b) > 0, то существует такое значение a переменного x, что a < a < b

и f(a) = 0.

Теорема Вейерштрасса о максимальном значении

Эта теорема утверждает: если функция f(x) непрерывна в интервале I, a 6

6 x 6 b, не исключая также и конечных точек интервала a и b, то

в интервале I должна существовать по крайней мере одна точка, в

которой функция f(x) достигает своего наибольшего значения M, и

другая точка, в которой функция f(x) достигает своего наименьшего

значения m. Говоря интуитивно, это значит, что график непрерывной

функции u = f(x) должен иметь по крайней мере одну наивысшую и

одну наинизшую точки.

Существенно отметить, что это утверждение может быть неверным,

если функция u = f(x) перестает быть непрерывной в конечных точ-

ках промежутка I. Например, функция f(x) = 1

x не имеет наибольшего значения в промежутке 0 < x 6 1, хотя она и непрерывна внутри проме-

жутка. И вместе с тем разрывная функция вовсе не обязательно достигает наибольшего и наименьшего значений, даже если она ограниченная

Определение производной

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.

Геометрический,механический,экономический смысл производной.

Геометрический смысл

Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке

Уравнение касательной к графику функции y = f(x) в точке x₀:

Механический смысл

Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан:  координата  x  движущейся точки – известная функция  x ( t ) времени  t. В течение интервала времени от  t₀  до  t₀ +   точка перемещается на расстояние:  x ( t₀ + )  x ( t₀ ) = , а её средняя скорость равна:  v_a =  . При  0  значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью  v ( t₀ )  материальной точки в момент времени  t₀ . Но по определению производной мы имеем:

отсюда,  v ( t₀ ) = x’ ( t₀ ) , т.e. скорость – это производная координаты по времени. В этом и состоит  механический смысл производной. Аналогично, ускорение – это производная скорости по времени:  a = v’ ( t )

Экономический смысл

Рассмотрим задачу о производительности труда. Пусть функция и = и (t) отражает количество произведенной продукции u за время ti необходимо найти производительность труда в момент t0.

За период времени от t0 до t0 + t количество произведенной продукции изменится от значения u0 = u (t0) до значения u0 + u = u (t0 + t), тогда средняя производительность труда за этот период времени zсер =. Очевидно, что производительность труда в момент t0 можно определить как предельное значение средней производительности за период времени от t0 до t0 + t при t à 0, т.е.

Таким образом, производительность труда есть производная от объема произведенной продукции по времени.

Дифференцируемые функции

Дифференци́руемая фу́нкция — это функция, имеющая дифференциал. Дифференцируемая функция может быть хорошо приближена линейной функцией. Дифференцируемость является одним из фундаментальных понятий в математике и имеет большое число приложений как внутри неё, так и в естественных науках, широко использующих математический аппарат (на данном отрезке).

Связь с существованием производной. непрерывность дифференцируемой функции.

Пусть на некотором промежутке Х определена функция y = f (x). Возьмём любую точку х₀ Х и зададим аргументу х в точке х₀ произвольное приращение Δ x такое, что точка х₀ + Δ x также принадлежит Х. Функция получит приращение Δy = f (x₀ + Δ x) − f (x₀).    Производной функции у = f (x) в точке х₀ называется предел отношения приращения функции в этой точке к приращению аргумента при Δ x → 0 (при условии, что этот предел существует)

.

   Правой производной функции у = f (x) в точке х ₀ называется предел отношения приращения функции в этой точке к приращению аргумента при Δ x → + 0 (при условии, что этот предел существует)

.

   Левой производной функции у = f (x) в точке х₀ называется предел отношения приращения функции в этой точке к приращению аргумента при Δ x → − 0 (при условии, что этот предел существует)

.

   Если левая производная функции у = f (x) в точке х₀ совпадает с правой производной функции у = f (x) в этой точке, то эти односторонние производные совпадают с самой производной функции в данной точке. Если для некоторого значения х₀ выполняется условие

(или ),

то говорят, что в точке х₀ функция имеет бесконечную производную знака плюс (или знака минус).

Непрерывность:

Если функция y = f (x) имеет производную в точке х = х₀, то говорят, что при данном значении аргумента х = х₀ функция дифференцируема.    Если функция дифференцируема в каждой точке интервала (a, b), то говорят, что она дифференцируема на этом интервале.    Если функция дифференцируема в некоторой точке х = х₀, то она в этой точке непрерывна.

Правила дифференцирования:производная суммы,произведения и частного

При дифференцировании константу можно выносить за производную: Правило дифференцирования суммы функций: Правило дифференцирования разности функций: Правило дифференцирования произведения функций (правило Лейбница): Правило дифференцирования частного функций: Правило дифференцирования функции в степени другой функции: Правило дифференцирования сложной функции: Правило логарифма при дифференцировании функции:

Производная сложной функции

Двухслойная" сложная функция записывается в виде

y=(fg)(x)=f(g(x))=f(u)

где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция также дифференцируема по x и ее производная равна

Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)!

Производная обратной функции

Дифференцируемая монотонная функция f: ]a, b[ → R с необращающейся в нуль производной имеет обратную дифференцируемую функцию f ^-1, производная которой вычисляется по формуле

Производная параметрической функции

Если функция f задана параметрически

x = φ(t), y = ψ(t), α < t < β,

где y = f(x) и функции φ и ψ дифференцируемы, причем φ'(t) ≠ 0, то

производные основных элементарных функций

Таблица производных

дифференциал,его геометрический смысл

Дифференциалом dy функции y=y(x) называется главная часть ее приращения, пропорциональная приращению  независимой переменно x. Дифференциал dx независимой переменной x равен ее приращению   : Дифференциал любой дифференцируемой функции y=y(x) равен произведению ее производной на дифференциал независмой переменной:

Геометрический смысл. На графике функции  (рис. 7.1.) возьмем произвольную точку . Дадим аргументу  приращение , тогда функция получает приращение . В точке  проведем касательную, образующую угол  с осью . Из треугольника : . Из  имеем: . Таким образом,  и соответствует формуле (7.1).

Инвариантность формы первого дифференциала

Рассмотрим сложную функцию y=f(u(x)). Пусть функции y=f(u), u=u(x) дифференцируемы, тогда Таким образом, если аргументом функции является функция другого аргумента, то форма дифференциала совпадает с формой дифференциала , когда аргументом функции является независимая переменная. Это свойство называется инвариантностью формы дифференциала.

Применение дифференциала в приближенных вычислениях

Пусть нам известно значение функции y₀=f(x₀) и ее производной y₀' = f '(x₀) в точке x₀. Покажем, как найти значение функции в некоторой близкой точке x. Как мы уже выяснили приращение функции Δyможно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dyили Δy»f'(x₀)·Δx. Т.к., по определению, Δy = f(x) – f(x₀), то f(x) – f(x₀)≈f'(x₀)·Δx. Откуда f(x) ≈ f(x₀) + f'(x₀)·Δx

производные и дифференециалы высших порядков

производные

Производной второго порядка от функции называется производная от ее производной:   . Аналогично определяют производную любого порядка:  .

дифференциалы

Рассмотрим дифференциал функции в произвольной точке промежутка : . Здесь - приращение независимой переменной, которое является числом и не зависит от . Сам же дифференциал есть функция от , и можно вычислить дифференциал от этой функции:  При этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле Аналогично вычисляется дифференциал любого порядка .

Формула Лейбница-это

формула, выражающая производную n-го порядкаот произведения двух функций через производные сомножителей:  

теоремы Ролля и условия монотонности функции

Пусть функция f (x) непрерывна на [a, b], дифференцируема на (a, b) и на концах отрезка принимает равные значения f(a) = f(b). Тогда существует точка c  (a, b), в которой f ' (c) = 0.   

Условия монотонности

• (Критерий монотонности функции, имеющей производную на интервале) Пусть функция непрерывна на (a,b), и имеет в каждой точке производную f'(x). Тогда

f возрастает на (a,b) тогда и только тогда, когда

f убывает на (a,b) тогда и только тогда, когда

• (Достаточное условие строгой монотонности функции, имеющей производную на интервале) Пусть функция непрерывна на (a,b), и имеет в каждой точке производную f'(x). Тогда

если то f строго возрастает на (a,b);

если то f строго убывает на (a,b).

• (Критерий строгой монотонности функции, имеющей производную на интервале) Пусть и всюду на интервале определена производная f'(x). Тогда f строго возрастает на интервале (a,b) тогда и только тогда, когда выполнены следующие два условия:

2.