
Матричное исчисление
.docМатричное исчисление
Обозначения, терминология
Матрица размеров
![]() -
система mn чисел (элементов матрицы),
расположенных в прямоугольной таблице
из m строк и n столбцов. Если m
= n, матрицу называют квадратной
матрицей порядка n. Обозначения:
-
система mn чисел (элементов матрицы),
расположенных в прямоугольной таблице
из m строк и n столбцов. Если m
= n, матрицу называют квадратной
матрицей порядка n. Обозначения:

или более кратко
![]() соответственно
соответственно
![]()
Две матрицы А и B
одинаковых размеров равны (запись А
= В), если
![]()
 - нулевая матрица,
- нулевая матрица,
 - матрица, противоположная матрице A,
- матрица, противоположная матрице A,
 - трапециевидная (ступенчатая) матрица
- трапециевидная (ступенчатая) матрица
![]()
![]() -
матрица-строка.
-
матрица-строка.
![]() -
матрица-столбец,
-
матрица-столбец,
 -
верхняя треугольная матрица,
-
верхняя треугольная матрица,
 -
нижняя треугольная матрица,
-
нижняя треугольная матрица,
 -
диагональная матрица,
-
диагональная матрица,
 -
скалярная матрица,
-
скалярная матрица,
 -
единичная матрица,
-
единичная матрица,
(кратко:
![]() где
где
 -
символ Кронекера).
-
символ Кронекера).
Если все
![]() действительны,
то матрица A называется действительной;
если хотя бы одно из чисел
действительны,
то матрица A называется действительной;
если хотя бы одно из чисел
![]() комплексное,
то матрица называется комплексной.
комплексное,
то матрица называется комплексной.
Сложение матриц
Суммой матриц
![]() и
и
![]() одинаковых
размеров называется матрица
одинаковых
размеров называется матрица
![]() тех
же размеров, у которой
тех
же размеров, у которой
![]() Обозначение:
C = А + В.
Обозначение:
C = А + В.
Свойства сложения
матриц: А + В = В + А, (А + В) + С = A + (B +
C), А + 0 = A, А + (-A) = 0,
![]() A,
B, C.
A,
B, C.
Вычитание матриц
А - В = А + (-В).
Умножение матрицы на число
Произведением матрицы
![]() на
число
на
число
![]() называется
матрица
называется
матрица
![]() тех
же размеров, у которой
тех
же размеров, у которой
![]() Обозначение:
Обозначение:
![]()
Свойства
![]() ,
,
![]()
![]()
![]() и
и
![]()
Умножение матриц
Произведением матрицы
![]() размером
размером
![]() на
матрицу
на
матрицу
![]() размером
размером
![]() назвается
матрица
назвается
матрица
![]() размером
размером
![]() у
которой
у
которой
 Обозначение:
C = AB.
Обозначение:
C = AB.
Свойства AE = EA = A, AO
= OA = O, (AB)D = A(BD),
![]() (AB)
= (
(AB)
= (![]() A)B
= A(
A)B
= A(![]() B),
(A + B)D=AD + BD, D(A + B) = DA + DB (при условии,
что указанные операции имеют смысл).
B),
(A + B)D=AD + BD, D(A + B) = DA + DB (при условии,
что указанные операции имеют смысл).
Для квадратных матриц
А и B, вообще говоря,
![]()
Транспонирование матриц

Свойства:
![]()
![]()
![]()
![]()
Специальные классы квадратных матриц
Симметрические матрицы:
![]()
![]() -
симметрическая
-
симметрическая
![]()
Кососимметрические
матрицы:
![]()
![]() -
кососимметрическая
-
кососимметрическая
![]()
Ортогональные матрицы:
![]()
![]() -
ортогональная
-
ортогональная

Невырожденные
(неособенные) матрицы:
![]()
Вырожденные (особенные)
матрицы:
![]()
Обратная матрица
Матрица
![]() -
обратная для матрицы A, если
-
обратная для матрицы A, если
![]()
Для квадратной матрицы
A обратная существует тогда и только
тогда, когда
![]()

где
![]() -
алгебраические дополнения элементов
-
алгебраические дополнения элементов
![]() матрицы
A.
матрицы
A.
Свойства:

Элементарные преобразования матрицы
Элементарными преобразованиями матрицы называют:
1) умножение какой-нибудь строки (столбца) на отличное от нуля число;
2) прибавление к какой-нибудь строке (столбцу) другой ее строки (столбца), умноженной на произвольное число;
3) перестановку местами любых двух строк (столбцов).
Вычисление обратной матрицы
Если с помощью элементарных
преобразований строк квадратную матрицу
A можно привести к единичной матрице
E, то при таких же элементарных
преобразованиях над матрицей E
получим
![]() .
.
Пример.
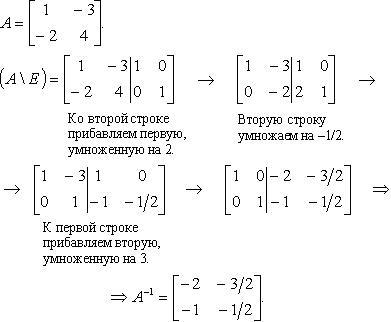
Ранг матрицы
Ранг матрицы - наивысший порядок отличных от нуля ее миноров. Обозначение: rank A.
Базисный минор матрицы - любой отличный от нуля минор порядка r = rank A.
Системы линейных уравнений
Общий вид системы

![]() ,
i = 1, 2, ..., m; j = 1, 2, ..., n, - коэффициенты
системы;
,
i = 1, 2, ..., m; j = 1, 2, ..., n, - коэффициенты
системы;
![]() -
свободные члены;
-
свободные члены;
![]() -
переменные;
-
переменные;
![]()
Если все
![]() =
0, система называется однородной.
=
0, система называется однородной.
Матричная запись системы линейных уравнений
AX = B,
где

Матрицу A называют матрицей (или основной матрицей) системы. Матрицу

называют расширенной матрицей системы,
а матрицу
![]() для
которой AС = В, - вектор-решением
системы.
для
которой AС = В, - вектор-решением
системы.
Критерий совместности линейных уравнений
Система совместна тогда и только тогда, когда rank A = rank D.
Правило Крамера
Если m = n и
![]() то
система совместна и имеет единственное
решение
то
система совместна и имеет единственное
решение
![]() или,
что то же самое,
или,
что то же самое,
![]() где
где
![]() -
определитель, полученный из det A
заменой i-го столбца столбцом
свободных членов.
-
определитель, полученный из det A
заменой i-го столбца столбцом
свободных членов.
Общее решение системы линейных уравнений
Если система линейных
уравнений AX = B совместна, rank A =
r и, например,
 -
базисный минор матрицы системы, то она
равносильна системе
-
базисный минор матрицы системы, то она
равносильна системе

Придавая переменным
![]() (свободным
переменным)
(свободным
переменным)
![]() получаем
однозначно (например, по правилу Крамера)
получаем
однозначно (например, по правилу Крамера)
![]() Тогда
Тогда
![]() -
решение исходной системы.
-
решение исходной системы.
Метод Гаусса
Метод Гаусса - метод последовательного исключения переменных. С помощью элементарных преобразований строк расширенной матрицы D системы матрицу A системы приводят к ступенчатому виду:

![]() Если
среди чисел
Если
среди чисел
![]() есть
отличные от нуля, система несовместна.
есть
отличные от нуля, система несовместна.
Если
![]() то:
то:
1) при r = n исходная система равносильна системе:

имеющей единственное решение (сначала
находим из последнего уравнения
![]() ,
из предпоследнего
,
из предпоследнего
![]() и
т. д.);
и
т. д.);
2) при r < n исходная система равносильна системе:

имеющей бесчисленное множество решений
(![]() - свободные переменные).
- свободные переменные).
Однородные системы линейных уравнений
Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rank A < n.
Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:

Тогда n - r линейно независимыми вектор-решениями будут:

а любое другое решение является их
линейной комбинацией. Вектор-решения
![]() образуют
нормированную фундаментальную систему.
образуют
нормированную фундаментальную систему.
В линейном пространстве
![]() множество
решений однородной системы линейных
уравнений образует подпространство
размерности n - r;
множество
решений однородной системы линейных
уравнений образует подпространство
размерности n - r;
![]() -
базис этого подпространства.
-
базис этого подпространства.
Определители
Определения
В перестановке
![]() чисел
1, 2, ..., n два числа
чисел
1, 2, ..., n два числа
![]() и
и
![]() составляют
инверсию, если i < j, но
составляют
инверсию, если i < j, но
![]() >
>![]() .
Число всех возможных инверсий данной
перестановки обозначают
.
Число всех возможных инверсий данной
перестановки обозначают
![]() Перестановку
называют четной, если I - четное
число, и нечетной, если I - нечетное
число.
Перестановку
называют четной, если I - четное
число, и нечетной, если I - нечетное
число.
Определитель (детерминант)
квадратной матрицы
![]() -
число (обозначение
-
число (обозначение
![]() )
)
![]()
где
 означает,
что суммирование производится по всем
перестановкам
означает,
что суммирование производится по всем
перестановкам
![]() чисел
1, 2, ..., n.
чисел
1, 2, ..., n.
В частности n = 2

при n = 3

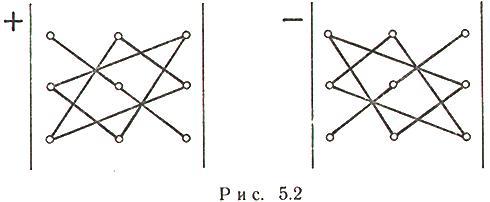
На рис. 5.2 проиллюстрирован закон, по которому составляется определитель матрицы третьего порядка: слева дано правило вычисления положительных членов определителя, справа - отрицательных.
Миноры определителя
Минор
![]() элемента
элемента
![]() определителя
определителя
![]() порядка
n - определитель порядка n - 1,
полученный из
порядка
n - определитель порядка n - 1,
полученный из
![]() вычеркиванием
i-й строки и j-го столбца.
вычеркиванием
i-й строки и j-го столбца.
Главные миноры определителя
Для
 главные
миноры есть определители
главные
миноры есть определители

Алгебраические дополнения
Алгебраическое дополнение
элемента
![]() определителя
определителя
![]() -
определитель
-
определитель
![]() где
где
![]() -
минор элемента
-
минор элемента
![]() .
.
Разложение определителя
По элементам i-й строки:
![]()
По элементам j-го столбца:
![]()
Например, при n = 4 разложение по первой строке

Свойства определителя
1.
![]()
2. Если все элементы какой-нибудь строки (столбца) определителя равны нулю, то определитель равен нулю.
3. Если матрица B
получена из матрицы A перестановкой
двух каких-либо ее строе (столбцов), то
![]()
4. Общий множитель всех элементов произвольной строки (столбца) определителя можно вынести за знак определителя.
5. Определитель, содержащий две пропорциональные строки (столбца), равен нулю.
6. Пусть
![]() -
квадратная матрица порядка n; k
- фиксированное натуральное число:
-
квадратная матрица порядка n; k
- фиксированное натуральное число:
![]() -
матрицы, которые получаются из A
заменой ее k-й строки (столбца)
соответственно строками (столбцами)
-
матрицы, которые получаются из A
заменой ее k-й строки (столбца)
соответственно строками (столбцами)
![]()
![]() Тогда
Тогда
![]()
7. Определитель не меняется от прибавления к какой-либо его строке (столбцу) другой его строки (столбца), умноженной на произвольное число.
8. Если какая-либо строка (столбец) определителя есть линейная комбинация других его строк (столбцов), то определитель равен нулю.
9.
![]()
