Свойства совершенства:

1) каждое логическое слагаемое, содержащее переменные, входит в функцию F(x₁, … , x_n);

2) все логические слагаемые формулы различны;

3) ни одно логическое слагаемое формулы не содержит одновременно переменную и ее отрицание;

4) ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.

Основная операция над функциями АЛ называется суперпозицией или операцией образования сложной функции. Смысл в том, что вместо переменных ставятся функции, и это может повторяться.

Элементарной дизъюнкцией (ЭД) системы x₁, x₂, …, x_n называется дизъюнкция некоторых переменных этой системы или их отрицаний.

Элементарной конъюнкцией (ЭК) системы x₁, x₂, …, x_n называется конъюнкция некоторых переменных этой системы или их отрицаний.

ЭД называется правильной, если каждая переменная входит в нее не более одного раза, включая и ее вхождение под знаком ¬.

Если в ЭД (ЭК) входит каждая высказывательная переменная системы с отрицанием или без него и притом только 1 раз, то она называется полной ЭД или ЭК.

Систему значащих высказывательных переменных, для которых данная ПЭД принимает значение 0, назовём нулем ПЭД.

Систему значащих высказывательных переменных, для которых данная ПЭК принимает значение 1, назовём ПЭК. (стр. 39, лекции С. Яблокова, автор кратких записей в сомнениях).

Теорема 1

Для того, чтобы ЭД была ТИ необходимо и достаточно, чтобы в ней содержались вместе с некоторой высказывательной переменной x_i, и ее отрицание ¬ x_i.

Теорема 2

Чтобы ЭК была ТЛ необходимо и достаточно, чтобы в ней содержалось хотя бы одна пара множителей, один из которых является отрицанием другого.

Формула A называется конъюнктивной нормальной формой (КНФ) системы высказывательных переменных x₁, x₂, …, x_n, если A является конъюнкцией элементарных дизъюнкций (ЭД) высказывательных переменных этой системы.

Формула А называется дизъюнктивной нормальной формой (ДНФ) системы высказывательных переменных x₁, x₂, …, x_n, если A является дизъюнкцией ЭК-ций высказывательных переменных этой системы.

Теорема 3

Для каждой формулы существует эквивалентная ей КНФ.

Формула А называется совершенной КНФ (СКНФ) от высказывательных переменных x₁, x₂, …, x_n, если она является конъюнкцией различных полных элементарных дизъюнкций от высказывательных переменных этой системы. При этом порядок членов в элементарных дизъюнкциях не учитывается.

Формула B называется СДНФ от высказывательных переменных x₁, x₂, …, x_n, если она является дизъюнкцией различных полных элементарных конъюнкций от x₁, x₂, …, x_n. Формула B – СДНФ, если B = A*для некоторой СКНФ формулы А.

СДНФ формулы А(x₁, x₂, …, x_n) обладает следующими свойствами:

1) в ней нет одинаковых слагаемых;

2) ни одно слагаемое не содержит 2-х одинаковых множителей;

3) ни какое слагаемое не содержит переменную вместе с ее отрицанием;

4) в каждом слагаемом содержится в качестве множителя либо x_i, либо ˥x_i.

Условия 1) – 4) являются необходимыми и достаточными, чтобы ДНФ была совершенной нормальной формой.

АЛ используется в релейно-контактных схемах.

Логическое следствие.

Теорема 1

A |= B  | = A –> B

Теорема 2

1) A₁, A₂, …, A_n |= B

2) A₁ Λ A₂ Λ … Λ A_n |= B

3) |= A₁ Λ A₂ Λ … Λ A_n -> B – общезначима

Следствие

Если А₁, А₂, …, А_n |= B, то A₁, …, A_n |= A_n -> B

Теорема 3

Из любых посылок вытекает любая другая.

Алгоритм распознавания логического следствия.

1. Предположим, что рассуждение не является логическим следствием, т. е. рассуждение нелогично:

A_i = 1 (i = 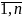), B = 0.

2. Подберем переменные, входящие в B таким образом, чтобы B = 0. будем подбирать значения других переменных так, чтобы все A_i = 1.

3. Возможны два случая:

а) удалось подобрать переменные согласно пункту 2;

значит, предположение верное, рассуждение нелогично;

б) не удалось подобрать переменные, и получилось противоречие;

значит, предложение было неверным, рассуждение логично.

Правила вывода

Правилами вывода математической логики называются правила, по которой из исходной истинности формул образуются новые истинные формулы.

Пусть А₁, А₂, …, А_n |= B

1. Сокращение посылки. Правило определения.

Пусть А = 1 и А -> B = 1, тогда можно вывести B:

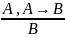
2. Цепное правило

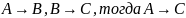
3. Правило подстановки

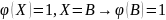
Множество {A₁, A₂, …, A_n} высказываний непротиворечиво, если А₁ Λ А₂ Λ … Λ А₃ = 1 по меньшей мере для одной комбинации, приписываемых простым компонентам истинностных значений. (т. е. то есть хотя бы для одной комбинации значений, приписываемых переменным А)

Множество {A₁, A₂, …, A_n} высказываний противоречиво, если А₁ Λ А₂ Λ … Λ А₃ = 0 для всех комбинаций истинных значений, приписываемые простым компонентам.

Противоречие – формула, которая всегда ложна. Например,

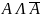
Множество {A₁, A₂, …, A_n} высказываний противоречиво, если из него в качестве логического следствия можно вывести противоречие.