Программирование

1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

1. Основные понятия теории алгоритмов

Алгоритмом часто называют конечную совокупность инструкций для решения некоторого класса задач. Это определение неформально, так как с его помощью нельзя однозначно ответить на вопросы, что такое “совокупность инструкций” и “некоторый класс задач”.

Для записи алгоритмов можно использовать обычный разговорный язык. В этом случае, например, алгоритм возведения числа X в целую положительную степень Y, т.е. вычисления по формуле S = X^Y можно записать в виде следующей системы последовательно выполняемых правил или указаний:

1. Присвоить переменной S значение “единица”. Перейти к пункту 2.

2. Присвоить переменной i значение “единица”. Перейти к пункту 3.

3. Если i Y, то перейти к пункту 4, иначе – к пункту 6.

4. Присвоить переменной S ее предыдущее значение, умноженное на величину X. Перейти к пункту 5.

5. Увеличить значение i на единицу. Перейти к пункту 3.

6. Считать значение S результатом. Вычисления прекратить.

Другой пример алгоритма – поиск минимального числа x в последовательности из n чисел a₁,a₂, ...,a_n. Пусть в качестве минимального числа x принимается а₁, после чего x сравнивается с последующими числами, начиная с а₂. Если x<a₂, то x сравнивается с а₃ и т. д., пока не найдется число a_i<х. Если a_i<x, то x присваивается значение a_i и продолжается сравнение x со следующими числами, начиная с a_i+1. Процесс продолжается до тех пор, пока не будут просмотрены все n чисел. В результате x будет иметь значение, равное наименьшему в последовательности числу. Этот процесс может быть записан в виде следующей системы последовательных указаний:

1. Положить x = a₁. Перейти к пункту 2.

2. Положить i = 2 . Перейти к пункту 3.

3. Если i  n, то перейти к пункту 4, иначе – к пункту 6.

4. Если a_i < x , то положить x= a_i. Перейти к пункту 5.

5. Увеличить i на единицу. Перейти к пункту 3.

6. Считать значение x результатом. Прекратить просмотр.

Алгоритмы, в соответствии с которыми решение задач сводится к арифметическим действиям, называются численными алгоритмами. Если решение задачи осуществляется с помощью логических действий, которые связаны с принятием решений на основе выполнения некоторых условий, то алгоритмы называются логическими. Эти определения также неформальны, так как при решении практических задач соответствующие им алгоритмы редко могут быть определены однозначно. Примерами логических алгоритмов могут служить поиск минимального числа в последовательности, поиск пути на графе, частотный анализ текстов и др.

Концепции алгоритмов в математических терминах были впервые описаны в 1930 - 1940 г.г., когда велись поиски условий, с помощью которых возможно доказательство проблемы разрешимости задач или, в общем случае, автоматическое доказательство математических теорем. Существуют три основных типа алгоритмических моделей [2]. В первом понятие алгоритм связывается с вычислимыми числовыми функциями. Во втором алгоритм представляется как некоторое универсальное устройство, способное выполнять набор простейших операций (например, машина Тьюринга). Третий тип основывается на ниже определяемых понятиях абстрактного алфавита и соответствия между словами в таком алфавите, что позволяет формально описывать процессы преобразования информации.

В современной математике алгоритмами принято называть конструктивно задаваемые соответствия между словами в абстрактных алфавитах. Это определение, в свою очередь, использует два понятия – понятие абстрактного алфавита и слов в таком алфавите.

Абстрактным алфавитом называется любая конечная совокупность объектов, называемых буквами или символами данного алфавита. Иными словами алфавит - это конечное множество различимых символов (слово "абстрактный" для краткости здесь и далее опускается). Алфавит, как и любое другое множество, может быть задан перечислением его элементов. Например, алфавит A есть A={a, bc}, алфавит B есть B={x, y}.

Под словом или строкой в алфавите понимают любую конечную последовательность символов. В последовательности (цепочке) между символами стоит операция сцепки или конкатенации, т.е. менять местами символы в последовательности нельзя. Например, в алфавите A словами являются любые последовательности: aac cbacb bb, а в алфавите B: x, y, yx, xx и т. п.

Число символов в слове называется длиной этого слова. Так слова в алфавите A, приведенные в примере, имеют длину соответственно 1, 2, 2, 3, 2. Различают также пустые слова, не содержащие ни одного символа. Слово p называется подсловом слова q, если слово q можно представить в виде q=pr, где r - любое слово, в том числе и пустое. Очевидно, что такое понятие слова будет отличаться от аналогичного в разговорных языках. Здесь под словом можно понимать любую последовательность символов, даже бессмысленную.

При расширении алфавита понятие слова может существенно меняться. Так, например, в алфавите A={0,1,2,3,4,5,6,7,8,9} цепочка символов 69+73 представляет собой два слова, соединенные знаком суммы, а в алфавите B={+,0,1,2,3,4,5,6,7,8,9} это будет одно слово. В общем случае, в качестве символов могут использоваться не только одиночные символы, но и отдельные слова, фразы, абзацы и, даже, целые тексты.

Алфавитным оператором или алфавитным отображением называется всякое соответствие между словами некоторого алфавита и словами в том же самом или в каком-либо другом фиксированном алфавите. Первый алфавит называется входным, а второй – выходным алфавитом данного оператора. В случае совпадения входного и выходного алфавитов говорят, что алфавитный оператор задан в соответствующем алфавите.

Пусть заданы слова в алфавитах X и Y и заданы соответствия между этими словами. Если x_i– слово в алфавите X, а y_j – слово в алфавите Y, то алфавитный оператор Гx_i=y_j преобразует входное слово x_i в выходное слово y_j. Символ Г в алфавитном операторе означает отображение.

Различают однозначные и многозначные алфавитные операторы. Под однозначным алфавитным оператором понимается такой алфавитный оператор, который каждому входному слову ставит в соответствие не более одного выходного слова.

Совокупность всех слов, на которых алфавитный оператор определен, называется областью его определения. Алфавитный оператор, не сопоставляющий данному входному слову a_i никакого выходного слова b_j (в том числе и пустого), на этом слове не определен.

К наиболее простым алфавитным операторам относятся так называемые посимвольные отображения. Последнее состоит в том, что каждый символ входного слова алфавита A заменяется некоторым символом выходного алфавита B. Более сложными являются так называемые кодирующие отображения. Под кодирующим отображением понимается соответствие, сопоставляющее каждому символу входного алфавита некоторую конечную последовательность символов в выходном алфавите, называемую кодом.

Пусть заданы алфавиты: A={p,r,s,t} – входной и B={a,b,c,d,f,g,h} – выходной. Тогда отображение символов А символами В, т.е. кодом (Рис.1.1), является примером кодирующего отображения. Для построения искомого отображения достаточно заменить все символы любого слова a_i в алфавите А соответствующими кодами алфавита В. Так, если слово x=sstr, то Гx=fghfghabcceg есть код исходного слова x.

Процесс, обратный кодированию, т.е. замена в слове b_j кодов алфавита В символами из А, называется декодированием и обозначается как Г^-1b_j=a_i. Например, для слова b=fghfghabcceg в алфавите В декодирование Г^-1b дает слово a=sstr.

Если при кодировании слова a_i получается некоторое слово b_j и декодирование дает исходное слово a_i(Гa_i=b_j, Г^-1b_j=a_i), то имеет место обратимость кодирования. Условие обратимости кодирования иначе называется условием взаимной однозначности соответствующего кодирующего отображения. В приведенном выше примере обратимость существует. Но, если зданы A={a,b,c}, B={r,s}, Га=r, Гb=s, Гс=rs и слово aabca в алфавите А, то обратимость отсутствует, так как Гaabca=rrsrsr, а Г^-1rrsrsr=aababa (либо одно из слов acaba, aabca, acca).

Для обратимости кодирования должны выполняться следующие условия:

• коды разных символов исходного алфавита А должны быть различны;

• код любого символа алфавита А не может совпадать ни с каким из начальных подслов кодов других символов этого алфавита.

Пояснение этих утверждений сводится к следующему. Пусть слово q=b₁,b₂, ...,b_n является кодом слова p=a₁,a₂, ...,a_m в алфавите А. Тогда по коду q можно однозначно восстановить слово р. В силу второго условия только одно начальное подслово слова q будет совпадать с каким-либо символом алфавита А. Ясно, что таким подсловом является символ а₁. Применяя аналогичные рассуждения к оставшемуся отрезку слова q, можно однозначно восстановить один за другим все символы слова р. Следовательно, любому данному коду может соответствовать только одно слово в А, что доказывает обратимость кодирующего отображения.

Второе условие обязательно выполняется в том случае, когда коды всех символов алфавита А имеют одинаковую длину. Кодирование, при котором все коды имеют одинаковую длину, называется нормальным.

Кодирование позволяет сводить изучение произвольных алфавитных отображений к алфавитным отображениям в некотором стандартном алфавите. Наиболее часто в качестве стандартного алфавита выбирается двоичный алфавит, состоящий из двух символов. В качестве таких символов обычно используются цифры 0 и 1, т.е. С={0,1}. Подавляющее большинство современных ЭВМ обрабатывают информацию, закодированную именно в двоичном стандартном алфавите.

Пусть А – произвольный, а С – стандартный алфавиты и n - число символов в алфавите А, а m - число символов в алфавите С. В этом случае всегда можно выбрать длину слова L, удовлетворяющую условию m^Ln и закодировать все символы в алфавите А словами длины l в алфавите С так, чтобы коды различных букв были разными (действительно, число различных слов длины L в m-символьном алфавите равно m^L). Любое такое кодирование будет нормальным и порождает обратимое кодирующее отображение слов в алфавите А в слова в алфавите С (см. ниже диапазон представления чисел в машине).

Понятие алфавитного оператора является чрезвычайно общим. К нему фактически сводятся или могут быть сведены любые процессы преобразования информации, поскольку символам алфавита можно поставить в соответствие объекты произвольной природы. Важно только то, что количество рассматриваемых объектов должно быть конечным.

Основой теории алфавитных операторов являются способы их задания. В случае, если область определения алфавитного оператора конечна, оператор может быть задан просто таблицей соответствия. В левом столбце такой таблицы выписываются все слова, входящие в область определения рассматриваемого оператора, в правом – выходные слова, получающиеся в результате применения оператора к каждому слову из левого столбца таблицы.

В случае бесконечной области определения алфавитного оператора задать его с помощью такой таблицы невозможно. В этом случае оператор задается системой правил p_i (p_i  P, P={p_i}, i=1,2, ...,n), позволяющей за конечное число шагов найти выходное слово, соответствующее любому наперед заданному входному слову из области определения рассматриваемого алфавитного оператора.

Формальное определение алгоритма

Как уже упоминалось алфавитные операторы, задаваемые конструктивно с помощью конечной системы правил, являются алгоритмами. При этом нужно помнить, что в понятии алфавитного оператора существенно лишь само соответствие, устанавливаемое между входными и выходными словами, а для алгоритма в первую очередь важен способ задания устанавливаемого им соответствия. Так два алфавитных оператора считаются равными, если они имеют одну и ту же область определения и сопоставляют любому наперед заданному входному слову из этой области одинаковые выходные слова. Два алгоритма считаются равными, если равны соответствующие им алфавитные операторы и совпадает система правил, задающих действие этих алгоритмов на входные слова, и эквивалентными, если у них совпадают алфавитные операторы, но не совпадают способы их задания.

Свойства алгоритма. Всякий алгоритм любому входному слову ставит в соответствие только одно выходное слово. Это одно из основных свойств алгоритма – формальность. Иначе это свойство называют детерминированностью или однозначностью.

К числу других свойств алгоритма относятся массовость и результативность.

Результативность алгоритма – свойство алгоритма, обеспечивающее получение результата через конечное число шагов. Иными словами, если любому из принадлежащих к области определения слов алгоритм через конечное число шагов сопоставит результирующее слово, то он обладает свойством результативности.

Свойство результативности определяет понятие области применимости алгоритма. Областью применимости называется множество слов, для которых алгоритм результативен.

Тогда массовость алгоритма – это применимость ко всей области его определения.

В этом случае эквивалентность алгоритмов может быть определена следующим образом: два алгоритма эквивалентны, если совпадают их области применимости и результаты переработки любого слова из этой области. Если области применимости совпадют частично, алгоритмы называют слабо эквивалентными.

Оценка сложности алгоритмов

С каждым алгоритмом обычно связывается интуитивное представление о их сложности, основанное на оценке количества необходимых преобразованй слов, а также количества и длины самих слов. Однако, интуитивное представление не позволяет однозначно выбрать для решения конкретной задачи один из множества эквивалентных алгоритмов или определить возможность применения данного алгоритма для ее решения. При формальной оценке сложности алгоритмов можно использовать следующие определения. Пусть:

• А – алгоритм решения некоторого класса задач и n-размерность одной задачи из этого клааса (в частном случае n может быть, например длинной последовательности в рассмотренном выше алгоитме, количеством слов в анализируемом тексте и т.п.);

• функция f_A(n) даст верхнюю границу для максимального числа основных операций, которые должен выполнить алгоритм А для решения любой задачи размерности n.

Тогда алгоритм называется полиномиальным, если f_A(n) растет не быстрее чем полином от n. В противном случае алгоритм А называется экспоненциальным. Так, функции типа kn, kn²,kn³,..., где k – коэфициент, могут рассматриваться как полиномиальные, а функции типа 2ⁿ, nⁿ, n!... как экспоненциальнные. Для достаточно больших n значение экспоненциальной функции всегда превышает значение полиномиальной функции. Для малых n это не всегда справедливо, но всегда есть такое n, для которого значение экспоненциальной функции превышает аналогичное для полиномиальной.

Время, затраченное на реализацию алгоритма, как функция размерности задачи называется временной сложностью алгоритма и обозначается как O[f_A(n)]. Применительно к решению задачи на ЭВМ это время является в большинстве случаев свойством самого алгоритма и слабо зависит от машины, на которой решается соотвтствующая алгоритму программа.

Кроме временной сложности алгортмов существуют и другие меры сложности. Так, сложность можно характиризовать числом операций N (применительно к конкретной ЭВМ) и общим объемом информации Р, т.е общим количеством слов, используемых при выполнении алгоритма. Тогда время его выполнения на конкретной ЭВМ связано с числом операций, а объем информации связан с объемом памяти, необходимой машине для реализации соответствующей программы. Следовательно, время реализации алгоритма есть функция T=f(N). При таком подходе значения Т и Р называют соответственно вычислительной и емкостной сложностью алгоритма.

Блок-схемы алгоритмов

Среди универсальных форм представления или записи алгоритмов можно выделить так называемые блок-схемы алгоритмов. Универсальность этой формы обусловлена тем, что в ней заранее не определяются абстракции, которые могут специфицироваться в блоках даже с применением обычного разговорного языка. Блоки являются всего лишь шаблоном для описания действий в процессе решения задачи, а связи между блоками определяют последовательность этих действий.

Такая форма часто используется в профессиональной среде программистов. Она позволяет с достаточной степенью свободы описывать решения, получаемые в процессе нисходящего проектирования алгоритмов и соответствующих им программ, абстрагируясь от средств, предоставляемых конкретным языком программирования. Палитра ее средств (допустимых шаблонов)в этом случае может быть достаточно широка, однако для записи алгоритмов необходимым является минимальное подмножество средств, т.е. только два вида блоков - операторный и условный.

Операторный блок – это прямоугоник, в который вписывается некоторое действие или выражение (Рис.1.2.а). Этот блок может иметь несколько входов и только один выход, что обеспечивает однозначность в определении последовательности выполняемых действий. Исключение составляют начальный и конечный блоки. Первый не имеет входов, второй – выхода.

Условный блок обозначается ромбом, в который вписывается некоторое условие. Поскольку результатом проверки условия может быть либо “да”, либо “нет” (“истина” или “ложь”, “0” или “1”), блок имеет два соответствующих этим ответам выхода (Рис 1.2.б).

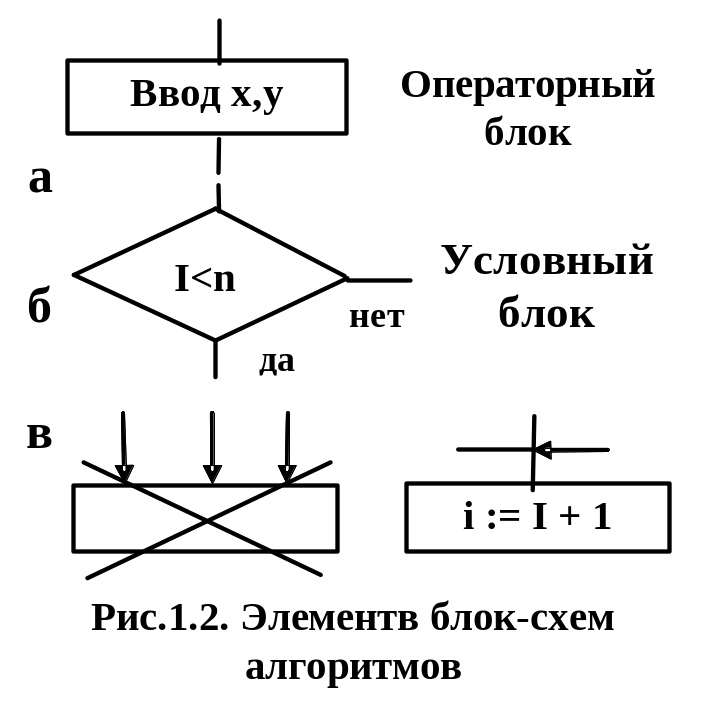
Если операторный или условный блоки имеют более одного входа, то изображение входов совмещается (Рис 1.2.в). На связях, определяющих последовательность выполнения блоков, стрелки не обязательны, если их направление сооветствует продвижению “сверху-вниз” и “слева-направо”. Ограничения на геометрические размеры блоков в этом случае не вводятся.

Такая форма представления алгоритмов очень удобнана в тех случаях, когда рассматриваются верхние уровни в иерархической структуре процесса проектирования программ и даже на нижних уровнях, если по каким-то причинам не определены средства их описания. Кроме того, блок-схемы наиболее удобны для записи алгоритмов на начальных стадиях обучения программированию.

Блок-схемы алгоритмов вычисления степенной функции и решения кваратного уравнения иллюстрируется соответствено рисунками Рис.1.3.а,б и 1.4.

Эта же форма описания алгоритмов принята для оформления программной документации. Набор блоков, используемый для документирования программ значительно шире и стандартизован.