3.7. Семейство кривых Пирсона

К. Пирсон в цикле работ начала нынешнего века предложил семейство кривых распределения столь же обширное, как и семейство кривых Джонсона. Это семейство кривых, полностью определяемое первыми четырьмя моментами, насчитывает 12 типов кривых, из которых обычно используют 7. Конкретный тип кривой устанавливают в зависимости от величины χ-критерия, который называют критерием Пирсона и определяют через величины μ₃ и μ₄ :

χ = (μ₃(s+2))/(16(s+1)), (3.34)

где

μ₃ и μ₄ - третий и четвертый основные моменты,

s=6(μ₄ - μ₃² - l)/(3μ₃²- 2μ₄ + 6).

Рис. 3.13.

С точки зрения практической аппроксимации наибольший интерес представляют следующие четыре типа асимметричных кривых (все они, за исключением кривых IV типа, могут быть U- и J-образные):

• I - случайная величина имеет размах, ограниченный с двух сторон, критерий χ<0, это - бета-распределение, рассмотренное выше;

• III—размах ограничен слева; критерий х = ±, практическое применение возможно при | χ |>4, это—гамма-распределение;

• IV—размах неограничен с обеих сторон, критерий χ заключен между 0 и 1;

• VI—размах ограничен с одной стороны (как правило, справа). Последний тип заменой у=а/х можно привести к первому типу, а непосредственное применение IV типа сопровождается определенными вычислительными трудностями.

В качестве основных обычно используют кривые I, IV и VI типов со значением критериев соответственно 0<χ<1 и χ>1, обеспечивающих по разнообразию форм кривых распределений потребности лесоводственной практики. Остальные типы - переходные на границах между I, IV и VI. Если χ=0 и ₄=0, то получают кривую нормального распределения, если χ=0, ₄<3 - типа II, если ₄>3 - VII, если χ = 1 - V.

Аппроксимацию кривыми Пирсона проводят в определенной последовательности:

1. по результатам наблюдений вычисляют первые четыре момента эмпирического распределения, на основе которых определяют критерий Пирсона и выбирают тип кривой распределения;

2. через эмпирические моменты выражают параметры кривой выбранного типа;

3. полученные параметры подставляют в уравнение соответствующего типа и вычисляют теоретические частоты.

Систематическое изложение техники аппроксимации по каждому типу семейства Пирсона достаточно громоздко, к тому же эти задачи, как и применение семейства кривых Джонсона, по своей трудоемкости требуют применения ЭВМ. В математическом обеспечении ЭВМ есть хорошие программы для автоматического поиска типа кривых и вычисления выравнивающих частот как одного, так и другого семейства.

Кривые семейства Пирсона неоднократно применяли в качестве универсальной модели распределения при решении многочисленных задач обработки лесоводственной информации. В качестве примера приведем схему вычислений выравнивающих частот ряда распределения диаметров стволов деревьев по уравнению Пирсона I типа, математическая модель которого имеет следующий вид:

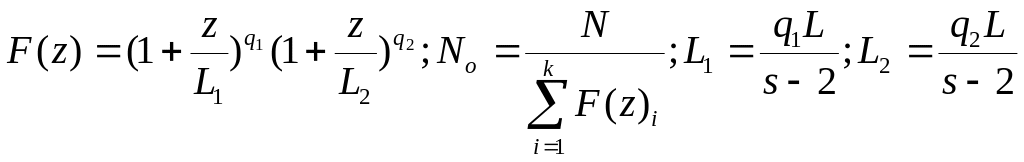( 3.35)

где

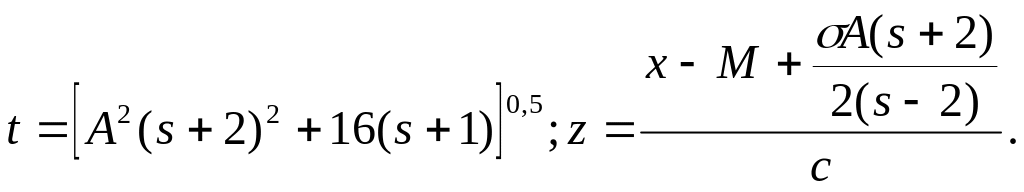
Здесь

 - среднеквадратическое отклонение;

A – коэффициент асимметрии;

E - коэффициент эксцесса

N - объем ряда распределения

n – выравнивающие частоты ряда.

Пример 3.10. Для ряда распределения (рис. 3.14) получены следующие статистики ряда распределения по толщине: n=313; M=26,492; =7,712; A=0,164; E=-0,251. Через полученные эмпирические моменты получаем по (3.35) параметры кривой f=-0,04; L=16,9719; L₁=6,7253; L₂=10,2466; q₁=9,4881; q₂= 6,2275; N_o=62,5. Далее полученные параметры подставляем в уравнение и вычисляем теоретические частоты.

Уравнения Пирсона I типа используются для “выравнивания” рядов, имеющих как резковыраженную положительную, так и близкую к нормальной ассиметрию. Наиболее часто эту модель применяют для рядов распределений деревьев по ступеням толщины при исследовании возрастной динамики древостоев.

Уравнения Пирсона I типа хорошо аппроксимируют резко асимметричные ряды распределения, как с положительной, так и с отрицательной асимметрией. Математическая модель этого уравнения имеет следующий вид:

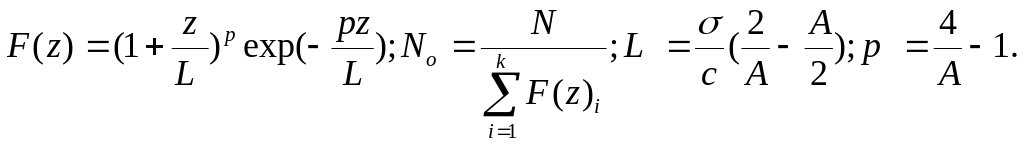( 3.36)

где

Пример 3.11. Для ряда распределения (рис. 3.15) получены следующие статистики ряда распределения деревьев по объему: n=313; M=0,625; =0,381; A=0,836; E=0,402. Через полученные эмпирические моменты получаем по (3.36) параметры кривой p=0,466; L=0,179; F(z)=4,810424; N_o=65,067. Далее полученные параметры подставляем в уравнение и вычисляем теоретические частоты с использованием MS Excel.

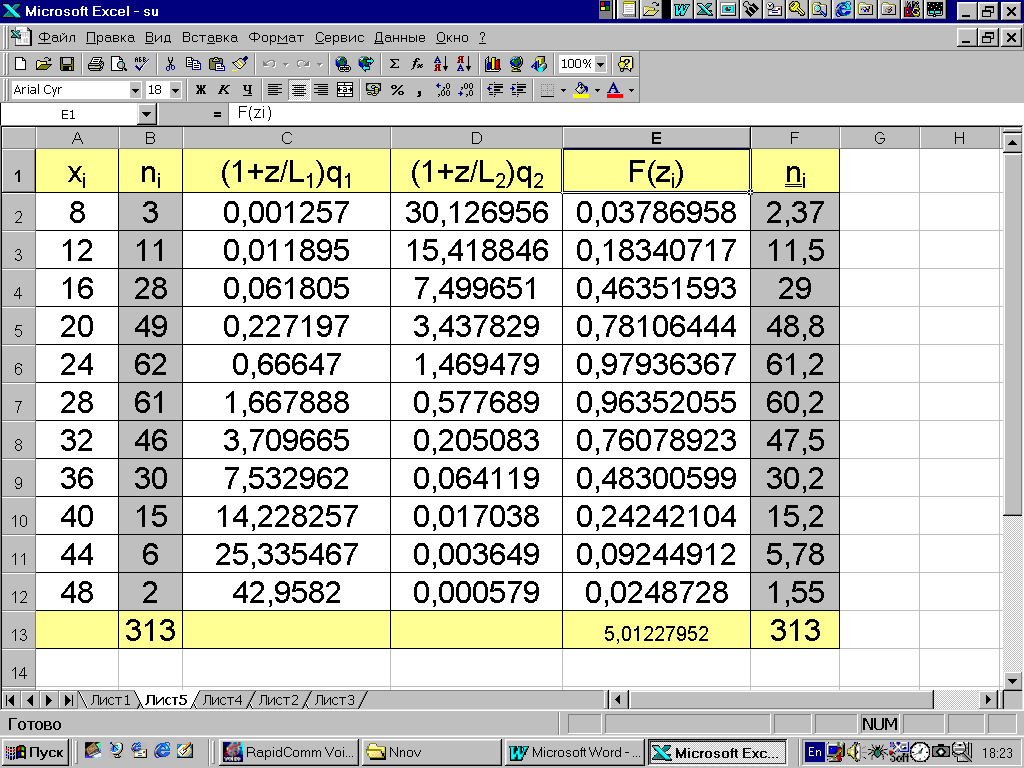
Рис. 3.14

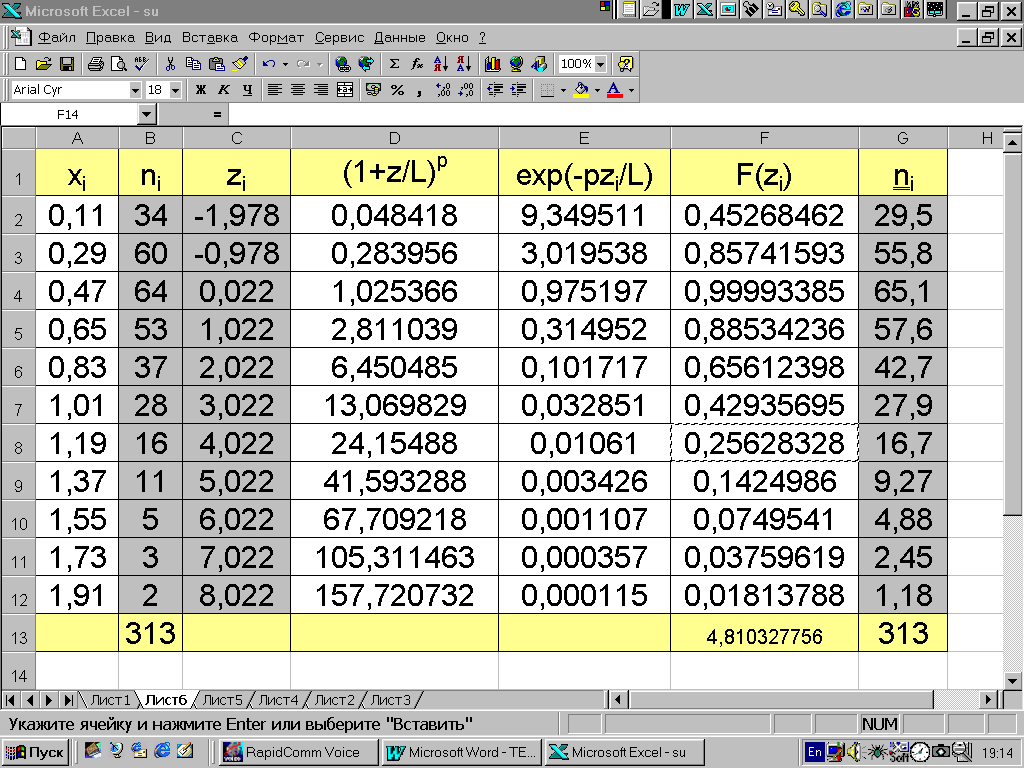
Рис. 3.15