3.2. Нормальное распределение

Этот тип непрерывного распределения, открытого в 1733 г. Муавром, имеет плотность распределения:

(3.1)

и функцию распределения (т. е. функцию накопленной вероятности):

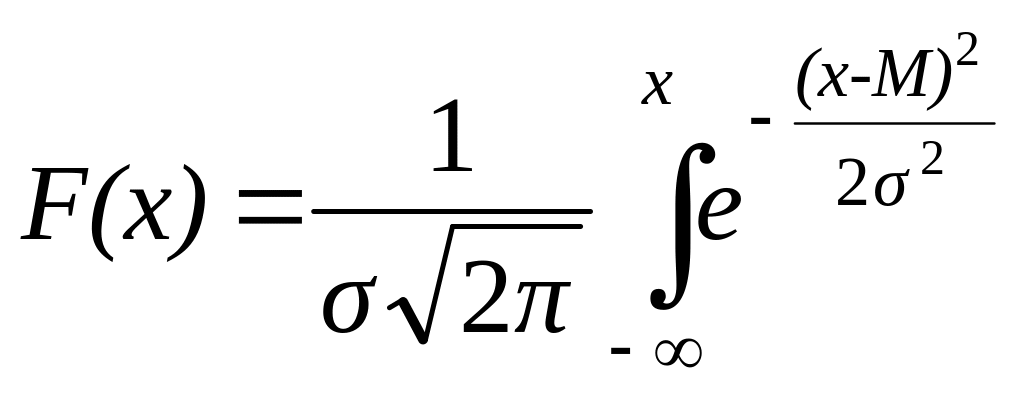, (3.2)

где

M - среднее значение;

 - среднее квадратическое отклонение.

Этими двумя параметрами нормальное распределение определяется однозначно, так как =3,142… и е=2,718... - общеизвестные константы.

Графически плотность распределения f(x) представляет собой симметричную относительно точки х = M колоколообразную кривую, форма которой зависит от величины среднего квадратического отклонения , являющегося параметром масштаба, а положение определяется величиной M (рис. 3.1). Кривая имеет один максимум 1/ , две точки перегиба на расстоянии ±σ от M и асимптотически приближается к оси х на ±. Пользуясь формулами (2.2), (2.13), можно выразить моменты нормального распределения через его параметры. В частности, имеем ₀=1, ₁==0, ₂=σ², ₃=0 (нулю равны все нечетные моменты), ₄=3σ⁴. Поэтому равенство нулю показателей косости и крутости - необходимое и достаточное условие, чтобы некоторое распределение было нормальным.

Закон нормального распределения играет особую роль как в теории статистического анализа, так и в его приложениях. Центральная предельная теорема утверждает, что распределение суммы независимых случайных величин (i=1,2, ..., N) стремится к нормальному при неограниченном увеличении n, если все величины имеют конечные средние и дисперсии и ни одна из них по своему значению резко не отличается от других.

Непосредственное вычисление вероятностей по (3.1) и (3.2) было достаточно трудоемкой операцией в эру отсутствия ЭВМ. Для "ручного" счета составить таблицы для всевозможных значений x и M было практически невозможным делом. Поэтому применялись таблицы значений f(x) и F(x), составленные для так называемого нормированного распределения, в котором M=0 (перенос точки отсчета) и σ = 1 (изменение масштаба). Конкретное распределение «нормируют» путем замены переменных

z = (x-M)/σ , (3.3)

Определение вероятности попадания любого взятого наугад дерева в заданный интервал подтверждается примером 3.1.

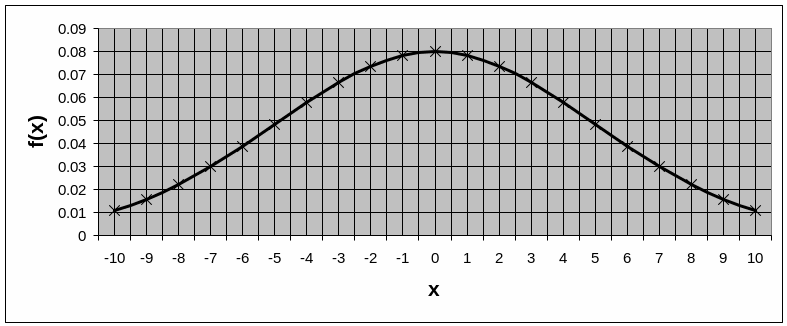
Рис. 3.1.

Пример 3.1. Диаметр деревьев в однородном древостое распределен по нормальному закону со средним M=35 см и =6 см. Определить вероятность того, что наугад взятое дерево попадает в интервал: 1) 30…40 см; 2) M±, 3) M±2, 4) M±3.

Решим поставленную задачу с использованием пакета MathCAD. Для определения первой вероятности проинтегрируем (3.1) в пределах от 30 до 40:

Таким образом, около 60% деревьев рассмотренного древостоя попадают в диапазон диаметров от 30 до 40 см. Аналогично производим расчеты для других трех случаев:

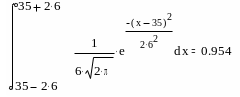
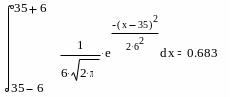
П 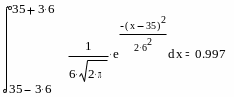оследние расчеты демонстрируют справедливость так называемых правил "одной сигмы", "двух сигм" и "трех сигм". Можно доказать, что в выборке достаточно большого объема из нормальной совокупности в среднем 68% наблюдений не отличаются от значения среднего больше, чем на величину ±σ. Аналогично имеем р(M—2σ<х<M+2σ)=0,95, для M±3σ -соответствующая вероятность - 0,997. Приведенное правило можно применять для приближенного решения ряда задач. Так, в большой выборке наименьшие и наибольшие значения случайной величины приближенно могут быть найдены как Х±3σ (правило трех сигм).

Расчет теоретических частот эмпирического ряда производят следующим образом:

1. Находят значения функции плотности вероятности нормального распределения (Приложение 2) для соответствующих величин нормирован-ного отклонения (3.3);

2. Вычисляют теоретические частоты ряда распределения n_i' по соответствующим данным объема выборки N, σ при величине классового промежутка i по формуле:

n_i' = . (3.4)

Наряду свычислением теоретических частот необходимо установить меру соответствия теоретически полученной кривой эмпирическому распределению по критерию χ² Пирсона (Приложение 3).

Пример 3.2. Вычисление теоретических частот n_i' и критерия соответствия эмпирического распределения нормальному χ²

Xi	ni	z	f(z)	n’i		ni - n’i	(ni - n’i)2
				Факт.	Округ.
8	2	2,07	0,04682	2,07	2	0	0	0
12	6	1,63	0,10567	4,66	5	1	1	0,2
16	10	1,18	0,19886	8,78	9	1	1	0,11
20	14	0,74	0,30339	13,39	13	1	1	0,08
24	16	0,30	0,39876	17,61	18	-2	4	0,22
28	18	0,14	0,39505	17,44	17	1	1	0,06
32	14	0,58	0,33530	14,81	15	-1	1	0,07
36	9	1,02	0,23713	10,47	10	-1	1	0,1
40	6	1,46	0,13542	5,98	6	0	0	0
44	3	1,91	0,06438	2,84	3	0	0	0
48	2	2,35	0,02522	1,11	1	1	1	1
Σ	100				99			χ2 = 1,84

см

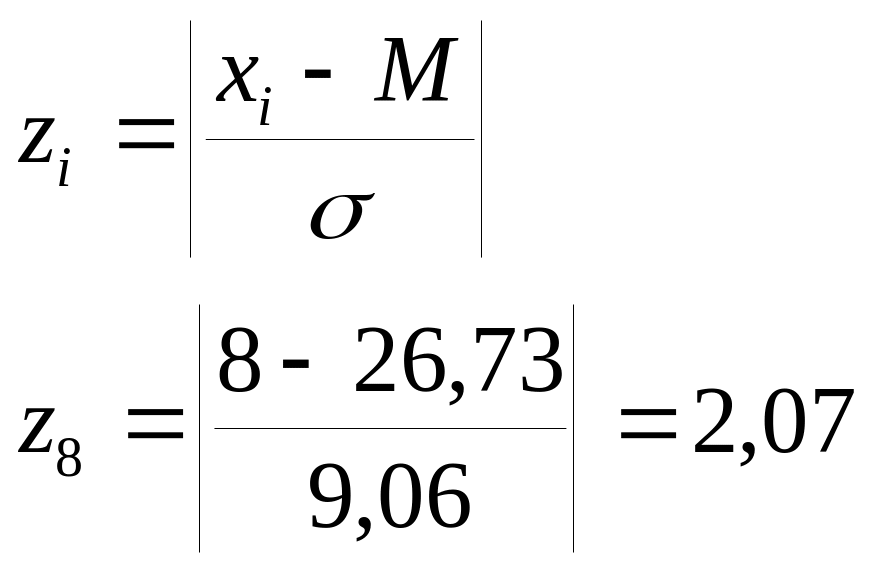
Cумма всех частных дает значение χ² = 1,84 при (11-3) = 8 степенях свободы вариации. Табличное значение =2,73 (по табл. Приложения 3). Так как =1,84 меньше =2,73, то делаем заключение о подчинении распределения эмпирических частот закону нормального распределения.

В целом предположение о том, что эмпирическое распределение строго соответствует нормальному закону, подтверждается относительно редко. Например, если в условиях, близких к требуемым по центральной предельной теореме, некоторые факторы влияют сильнее, чем другие, то распределение случайной величины становится несимметричным, хотя кривые распределения напоминают общие контуры нормальной кривой. Такие распределения (близкие к нормальным) обычны для лесного опытного дела. Далее рассмотрим одно из такого рода распределений – логарифмически нормальное.