12. Приложение производной к решению задач.

1.Составление уравнений касательной

Уравнение касательной к гр.ф-и y=f(x) в точке х=а y=f(a)+ f ’(a) (x-a) (*)

Алгоритм составления уравнения касательной к гр-ку фун-и y=f(x)

1. Обозначить абсциссу точки касания буквой а.

2. Вычислить f(а).

3. Найти f'(x) и вычислить f'(a).

4.Подставить найденные числа а, f(а), f '(а) в формулу y=f(a)+ f ’(a) (x-a).

Пр 1. Составить ур-е касс-й к гр. ф-и у =1/х в точке х = 1.

Реш-е. Восп-ся алгоритмом, учитывая, что в данном примере f(x)= 1/х.

1. а = 1.

2. f(a)= f (1)=1/1=1.

3. f ’(х)=- 1/х² ; f '(a) = f '( 1) = - 1/1² = -1.

4. Подставим найденные числа a = 1, f(a) = 1, f'(a) = -1 в формулу y=f(a)+ f ’(a) (x-a). По­лучим

y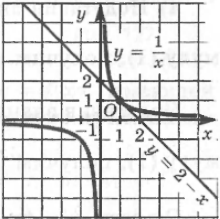 = 1 -(х- 1), у = 2-х.

На рис.изображена гипербола у =1/x, построена прямая у = 2-х. Чер­теж подтверждает приведенные выклад­ки: действительно, прямая у=2-х ка­сается гиперболы в точке (1; 1).

Ответ: у= 2-х.

Пр 2. К гр. ф-и у =x³/3 провести кас-ю так, чтобы она была параллельна прямой у = 4х — 5.

Реш-е. Требование «провести касательную» обычно означает «составить ур-е кас-й».

Воспользуемся алгоритмом составления ур-я кас-й. Здесь имеется неясность: не указана явно абсцисса точки касания.

Начнем рассуждать так. Искомая касательная д.б. парал-на пр. у = 4х- 5. Две прямые параллельны т.ит.т., когда равны их угловые коэффициенты. Зн-т, угл. коэф-т кас-й д.б равен угл.коэф-у заданной прямой: k_кас = 4. Но по геом.смыслу k_кас = f '(а). Т.о., значение а мы можем найти из уравнения f'(a) = 4.

Имеем: f '(x) =( x³/3)’=1/3 *3x² = x²; f'(a) = a².

Т.к. f '(a) = 4, т. е. а² = 4 находим а₁ = 2, а₂ = -2. Зн-т, им-ся 2 касат-е, удовл-е условию за­дачи: одна в точке с абсциссой 2, др. в точке с -2.

Теперь по алгоритму:

1. а₁ = 2, а₂ = -2

2. f(a₁)=2³/3=8/3;

f(a₂)=(-2³)/3=-8/3.

3. f '(a₁)= f '(a₂)=4.

4.Подставим значения

а₁ = 2, f(a₁)=8/3, f '(a₁)= 4 в y=f(a)+ f ’(a) (x-a) (*), у₁=8/3+4(х-2), у₁=4х-16/3.

а₂=-2, f(a₂)=-8/3, f '(a₂)=4 в (*) у₂=-8/3+4(х+2), y₂=4x+16/3

Отв. у=4х-16/3, y=4x+16/3

2.Исследование фун-и на монотонность и экстремумы

Алгоритм исслед. непрерывной ф-и у=f(х) на монотон-ть и экстремумы.

1.Найти производную f’(x).

2.Найти стационарные и критические точки.

3.Отметить стационарные и критические точки на число­вой прямой и определить знаки производной на полу­чившихся промежутках.

4.Опираясь на теоремы из § 35см.ниже, сделать выводы о моно­тонности функции и о ее точках экстремума.

Заметим, что если заданная функция имеет вид у=p(x)/q(x),то полюсы функции, т. е. точки, в которых знаменатель q(x) обращается в 0, тоже отмечают на числовой прямой, причем делают это до определения знаков производной. Но, разумеется полюсы не могут быть точками экстремума.

Пр. 6. Исследовать функцию у=(х⁴+16)/x² на монотонность и экстремумы.

Реш. Заметим, что фун-я всюду непрерывна, кро­ме точки х = 0. Восп-ся алгоритмом.

1.Найдем производную заданной функции: f ’(x)= =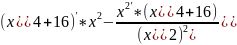

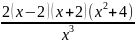
1) а = 1. 192

2) f(a)= f (1)=1/1=1. 192

3.Нахождение наибольшего и наименьшего значений непрерывной функции у= f(x) на отрезке [а,b] 194

f(x)≈ f(x₀)+ f '(x₀)∆x (1) 195

= ≈2(1+)= 2,02. 196

2. f '(x)=0 в точках х = 2 и х = -2 - это стационарные точки. Производная не существует в точке х = 0, но это не критическая точка, это точка разрыва функции (полюс).

3. Отметим точки -2, 0 и 2 на числовой прямой и расставим знаки производной на получившихся промежутках

↘ ↗ ↘ ↗

4.Делаем выводы: на луче(-∞; -2] функция убывает, на полуинтервале [-2; 0) функция воз­растает, на полуинтервале (0; 2] функция убывает, на луче [2; +∞) функция возрастает.

Далее, х = -2 — точка минимума, причем y_min = 8 (подставили значение х = -2 в формулу у=(х⁴+16)/x² )

Аналогично устанавливаем, что и х = 2 — точка минимума, причем у_min = 8.

Теоремы §35

Т1.(Т2) Если во всех точках открытого промежутка Х вып-ся нерав-во f ’(x)≥0 (f ’(x)≤0) (причем рав-во f ’(x)=0 выполняется лишь в отдельных точках и не вып-ся ни на каком сплошном промежутке), то фун-я у= f(x) возрастает (убывает ) на промежутке Х.

Т3. Если во всех точках открытого промежутка Х вып-ся рав-во f ’(x)=0, то фун-я у= f(x) постоянна на промежутке Х.

Опр.1 Точку х=х₀ наз. т. минимума функ-и у= f(x), если у этой тчк сущ-т окрестность, для всех тчк которой (кроме самой т. х=х₀) вып-ся равенство f(x)>f(x₀)

Значение фун-и в т.мин-ма обознач. y_min

Опр.2 Точку х=х₀ наз. т. максимума функ-и у= f(x), если у этой тчк сущ-т окрестность, для всех тчк которой (кроме самой т. х=х₀) вып-ся равенство f(x)<f(x₀)

Значение фун-и в т.макс-ма обознач. y_max

Тчк мин-ма и макс-ма фун-и объединяют общим термином – точки экстремума (от латин. «крайний»)

Т4.Если ф-я у= f(x) имеет экстремум в т. х=х₀ , то в этой тчк производная фун-и либо = 0, либо не сущ-т.

Внутренние тчк области опр-я фун-и, в кот. производная=0, наз.стационарными, а внутрен.тчк.обл.опр. фун-и, в которых фун-я непрерывна, но производная не сущ-т- критическими.

T6. (Достаточные условия экстремума)

Пусть фун-я у= f(x) непрер-на на промежутке Х и имеет внутри пром-ка ста стационарную или критическую т. х=х₀. Тогда :

А) если у этой т. сущ-т такая окрестность, в кот. при . х<х₀ вып-ся нерав-во f ’(x)<0, а при х>х₀ - f ’(x)>0, то х=х₀ - тчк мин-ма фун-и у= f(x);

Б) если у этой т. сущ-т такая окрестность, в кот. при . х<х₀ вып-ся нерав-во f ’(x)>0, а при х>х₀ - f ’(x)<0, то х=х₀ - тчк макс-ма фун-и у= f(x);

В) если у этой т. сущ-т такая окрестность, что в ней и слева, и справа от т.х₀ знаки производной одинаковы, то в т.х₀ экстремума нет.

3.Нахождение наибольшего и наименьшего значений непрерывной функции у= f(x) на отрезке [а,b]

1.Если функция непрерывна на отрезке, то она достигает на нем и своего наибольшего и своего наи­меньшего значений.

2.Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.

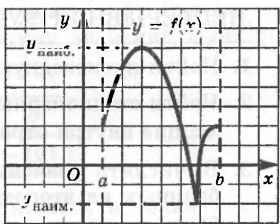
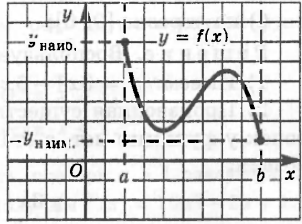
3. Если наибольшее (или наименьшее) значение достигает­ся внутри отрезка, то только в стационарной или критиче­ской точке.

В этом нет ничего удивительного, поскольку в этом случае наибольшее (или наименьшее) значение функции одновременно является экстремумом, а экстремум достигается только в ста­ционарной или критической точке.

Алгоритм отыскания наим-го и наибол-го значений непрерыв. фун-и у=f(x)на отр.[a,b]

1. Найти производную f'(x).

2.Найти стационарные и критические точки функции, ле­жащие внутри отрезка [а; b].

2. Вычислить значения функции у = f(x) в точках, ото­бранных на втором шаге (п. 2), и в точках а и b; вы­брать среди этих значений наименьшее (это будет y_нaим.) и наибольшее (это будет у_наиб.).

Мы приводим два примера, из которых второй — для тех, кому интересны математические «изюминки».

Пр 1. Найти наименьшее и наибольшее значения функ­ции у = х³ - 3х² - 45х + 1:

а) на отрезке [-4; 6]; в) на отрезке [—2; 2].

б) на отрезке [0; 6];

Решение. Воспользуемся алгоритмом.

1. Имеем: у' = 3х² - 6х -45.

2. Производная существует при всех х, значит, критических точек у функции нет, а стационарные найдем из условия у' = 0. Имеем:

3х² — 6х - 45 = 0; х² -2х - 15 = 0; х₁=- 3, х₂ =5

Дальнейшие рассуждения зависят от условий задачи.

а) Обе стационарные точки (и х₁=- 3, и х₂ =5) принадлежат заданному отрезку [-4; 6]. Значит, на третьем шаге алгоритма мы составим такую таблицу значений функции у = х³ - 3х² - 45х + 1::

X	-4	-3	5	6
У	69	82	-174	-161

Т. о., у_наим. = -174 (достигается в точке х= 5); у _наиб. =82 (достигается в точке х = -3).

б) Отрезку [0; 6] принадлежит лишь одна из двух найден­ных стационарных точек, а именно точка х = 5. Значит, на третьем шаге мы составим такую таблицу значений функции у = х³ - 3х² - 45х + 1::

X	0	5	6
У	1	-174	-161

Таким образом, у_наим. = -174 (достигается в точке х = 5); у _наиб. = 1 (достигается в т. х = 0).

в) Отрезку [-2; 2] не принадлежит ни одна из найденных стационарных точек, значит, достаточно вычислить значения функции в концевых точках: f(-2) = 71, f(2)=-93.

Т.о., в этом случае у_наим. = -93, у_наи6. - 71.

Теорема1. Пусть функция у = f(x) непрерывна на промежут­ке X и имеет внутри него единственную стационарную или кри­тическую точку х - х₀. Тогда:

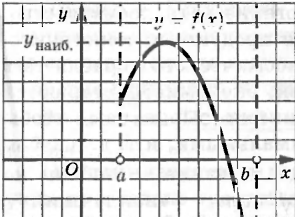
а) если х = х₀ — точка максимума, то у_наи6. = f(x₀);

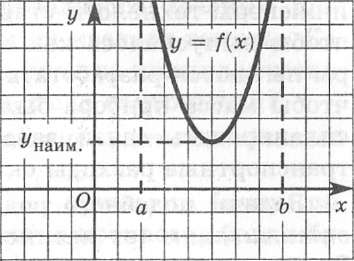
б) если х = х₀ — точка минимума, то у_наим. = f(x₀).

На рис. приведены соответствующие геометриче­ские иллюстрации.

Пр 3. Найти наибольшее значение функции 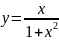на луче [0; + оо).

1. у'=

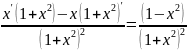
2. Производная всюду существует, зн-т, критических точек у функции нет.

Стационарные точки найдем из соотношения у' = 0. 1 - х² = 0 => х = 1 или х = -1. Задан­ному лучу [0; +оо) принадлежит лишь т. х = 1.

3.При х < 1 имеем у' > 0, а при х > 1 имеем у' < 0. Значит, х = 1 — точка максимума функции, причем y_max =f(1) = 1/(1+1²)= 1/2.

Т.к. х = 1 — единст-ая стационарная точка функ­ции на заданном промежутке, причем точка максимума, то, по теореме 1,

У _наиб.= У _max =f(1) =1/2 •

Рис. 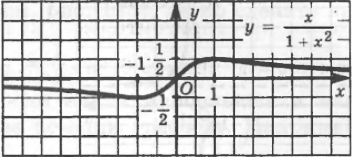хорошо иллюстрирует полученный результат.

Ответ: y_наиб. =1/2