3.Дайте определение отрезка, луча. Напишите задающее их ур-ние и неравенство в r3. Как проверить, лежит ли точка на заданном отрезке? Приведите примеры.

Отрезком в Rn, соединяющим точки P и Q, называется множество всех точек вида , причем P и Q концы.

Лучом в Rⁿ с началом в точке P называется множество всех точек вида

№8.

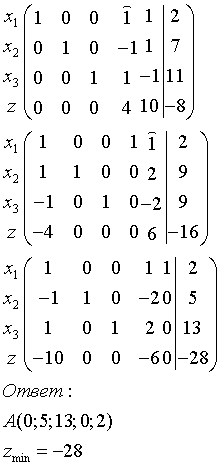
Билет 13.

№1.

Чтобы вычислить модель n-й степени комплексного числа z, используется формула Муавра:

.

Обоснование:

Чтобы изобразить на комплексной плоскости числа , нужно изобразить на плоскости точки с координатами (3;1) и (1;3) и соединить с началом координат. Получилось два вектора, изображённых на плоскости. Теперь вычислим сумму и произведение этих векторов аналитически:

Следовательно, вектор суммы изображается на плоскости как вектор, соединяющий начало координат и точку с координатами (4;4), а вектор произведения соединяет начало координат и точку с координатами (0;10).

№2.

Множество квадратных матриц порядка 2 будет называться линейным пространством, если на нём определены две операции:

• Сложение векторов

• Умножение вектора на число

Рассмотрим свойство, данное в задании.

След каждой матрицы (сумма элементов главной диагонали) Tr A=0, следовательно,

и т.д., в зависимости от количества таких матриц, составляющих множество линейного пространства.

В новой матрице, образованной из суммы данных матриц, получим:

.

Т.е. две операции, входящие в необходимое условие существование линейного пространства, определены. Следовательно, множество квадратных матриц порядка 2, обладающих вышеназванным свойством, образуют линейное пространство.

Базис данного пространства может выглядеть так:

.

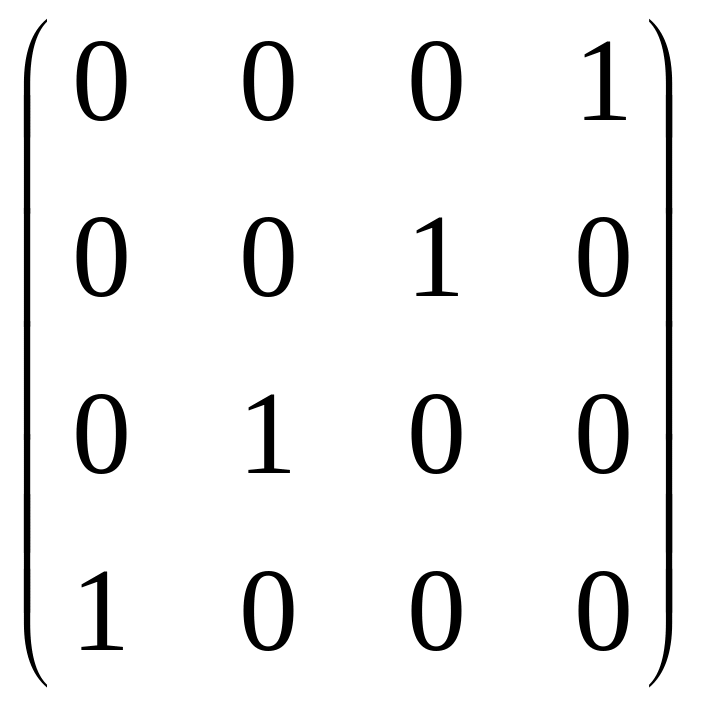№3.

Множество всех точек плоскости, координаты которых удовлетворяют алгебраическому уравнению 2-ой степени

называется кривой второго порядка.

Данные уравнения задают окружности. Чтобы схематично изобразить их графики, нужно подсчитать контрольные точки, выразив y через x и подсчитав их координаты.

№5.

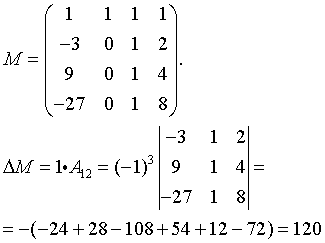
Билет №14.

№1.

Каноническим видом квадратичной формы называется такой вид, когда в новом выражении отсутствуют члены с произведениями различных координат.

Нормальным видом квадратичной формы называется вид, характеризующийся тем, что входящие в него квадраты переменных имеют коэффициенты плюс и минус единица.

Данной квадратичной форме отвечает матрица:

.

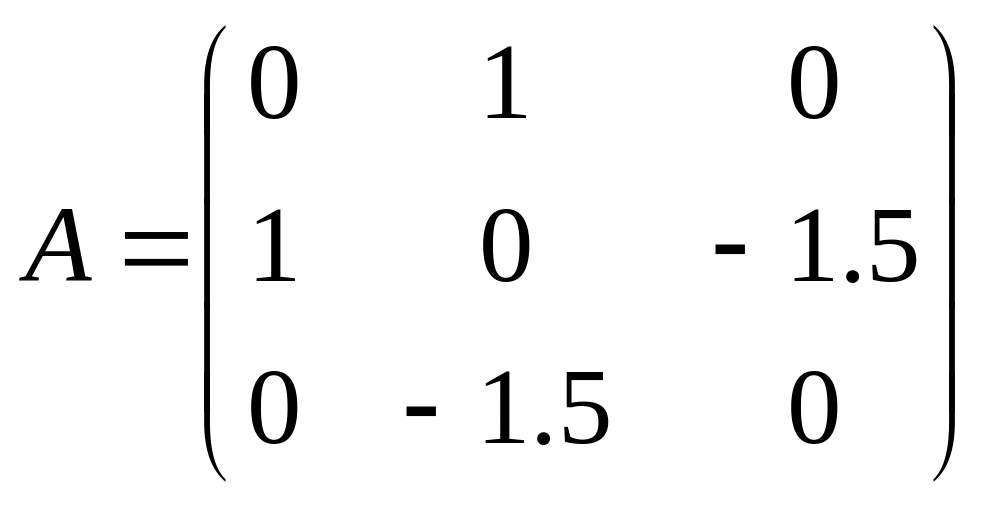Она имеет собственные значения:

Теорема приведения квадратичной формы к главным осям: для всякой симметрической матрицы можно найти такую ортогональную матрицу Q, которая приводит матрицу A к диагональному виду, т.е. матрица Q^-1AQ, полученная трансформированием матрицы A матрицей Q, будет диагональной.

№2.

Векторы называются коллинеарными, если и для некоторого числа k.

Система, содержащая коллинеарные векторы, линейно зависима:

, .

Из определения линейной зависимости следует: существуют такие , что справедливо равенство

Это равенство выполняется при условии коллинеарности векторов, следовательно, система, содержащая коллинеарные векторы, линейно зависима, а значит, вектора системы тоже линейно зависимы.

№3.

Основные теоремы двойственности.

1. Если исходная задача имеет оптимальное решение, то и двойственная ей также имеет оптимальное решение. При этом оптимальные значения целевых функций обеих задач равны.

2. Оптимальные решения пары двойственных задач связаны между собой следующими равенствами:

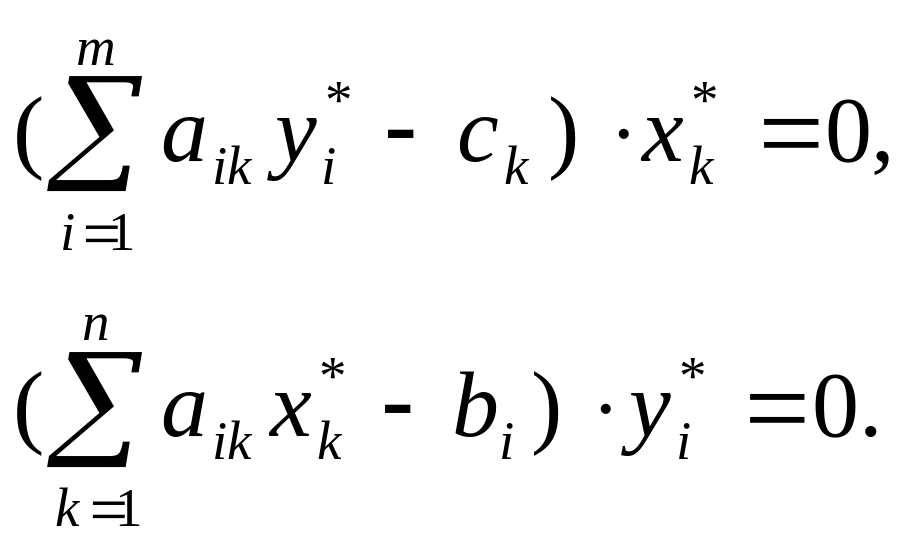
Чтобы найти решение двойственной задачи из последней симплексной таблицы исходной задачи, можно воспользоваться двумя формулами:

где - вектор индексной строки, координаты которого соответствуют базисным переменным исходной таблицы; - вектор с теми же координатами целевой функции соответственно; - вектор-строка, координаты которого равны коэффициентам целевой функции исходной задачи при базисных переменных последней симплексной таблицы; - матрица, столбцы которой соответствуют базисным переменным оптимального решения.

Билет №15.

№1.

Длину вектора называют модулем этого числа z. Пусть - отличное от нуля комплексное число, тогда из определения следует, что

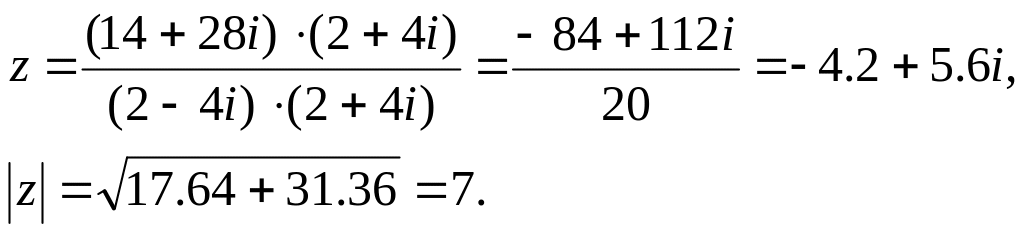
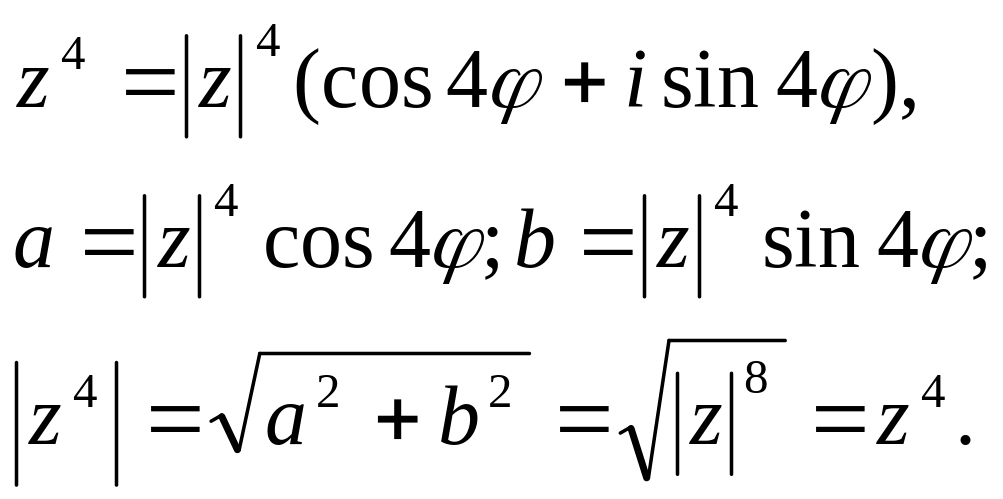
№2.

Если ФНР однородной системы линейных уравнений дан, то можно описать множество решений этой системы:

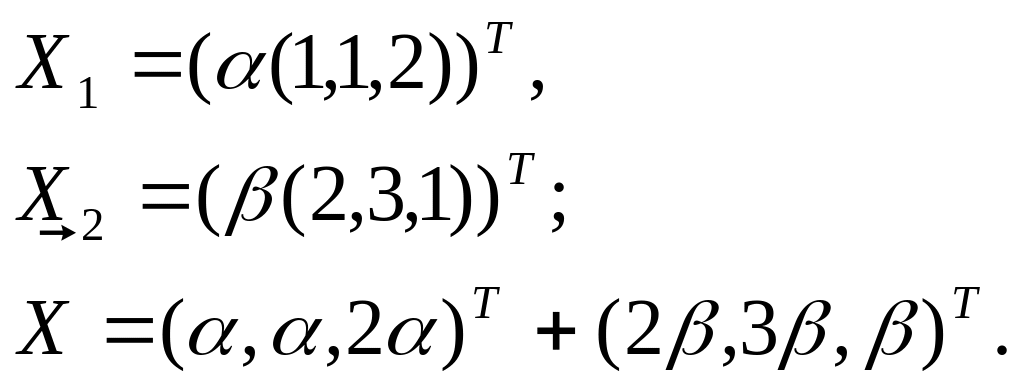
Минимально возможное число уравнений в такой системе равно 3-ём.

№3.

Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), лежащей в той же плоскости, что и кривая.

Окружность является частным случаем эллипса, когда большая и малая полуоси равны, с = 0, фокусы сливаются в центр. Эксцентриситет окружности равен нулю:

Каноническое уравнение эллипса выглядит так:

Из условия, что эксцентриситет окружности равен нулю, следует:

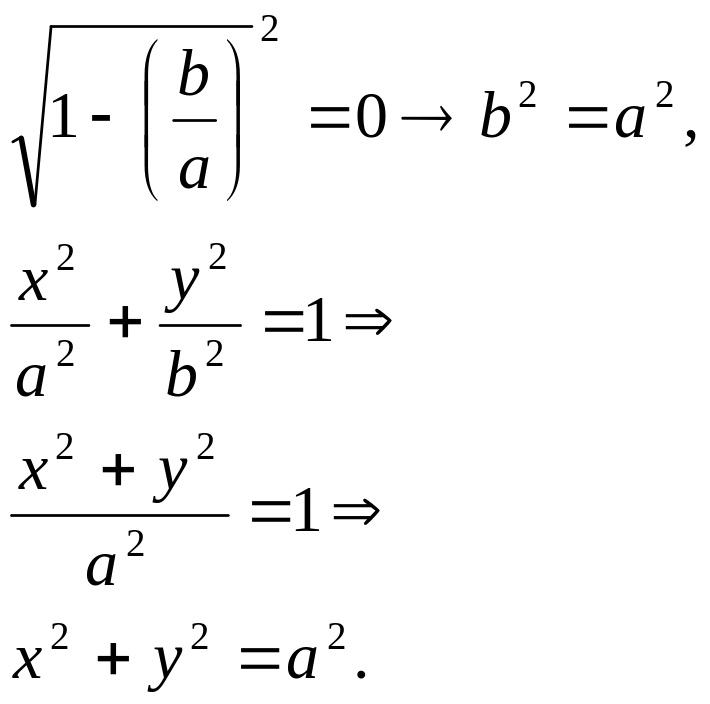
Следовательно, каноническое уравнение окружности выглядит так:

.

Билет №16.

№1.

Если ввести в рассмотрение матрицу:

,

а также матрицы

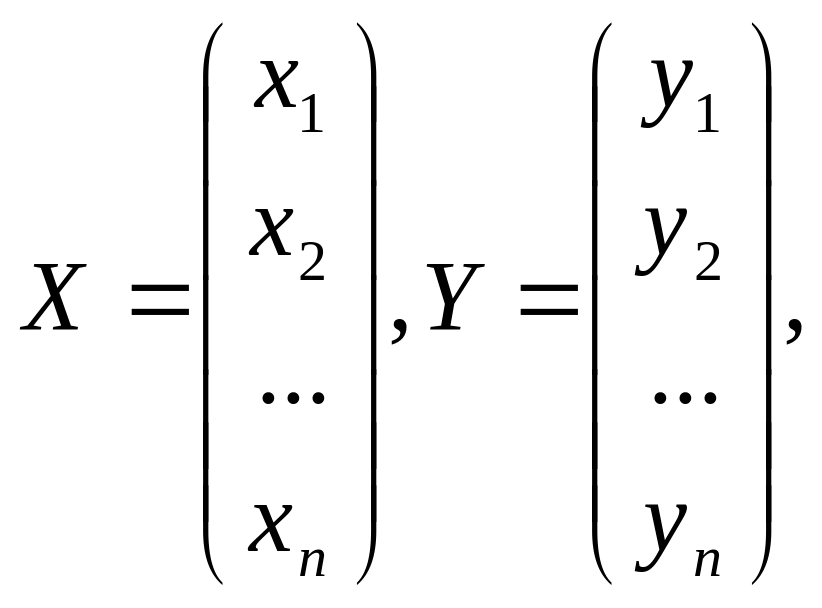то формулу можно записать следующим образом:

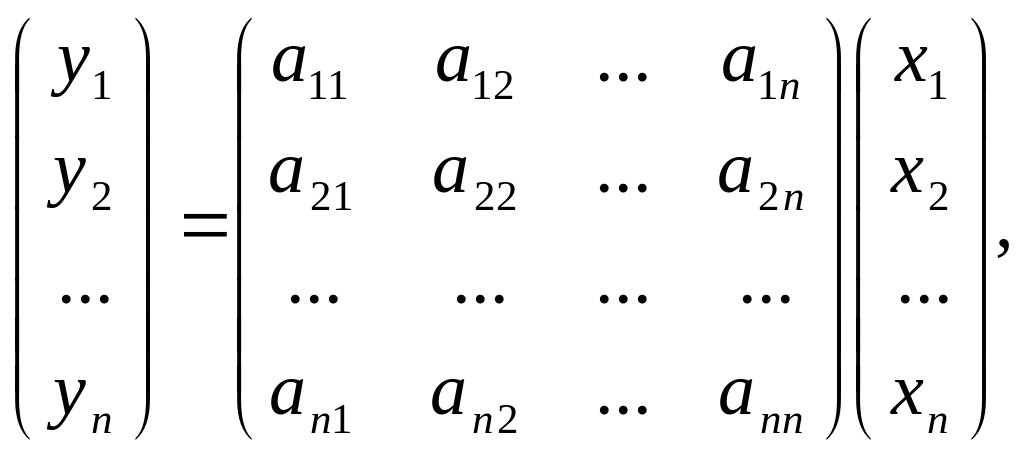
или сокращенно, в виде матричного равенства

Матрица A называется матрицей линейного преобразования f в данном базисе

Матрица поворота R² на данный угол в каноническом базисе имеет вид:

№2.

Из свойства определителя матрицы следует, что если одна из строк определителя есть линейная комбинация других строк, то определитель равен нулю.

Следовательно, рассматривая линейно независимые строки матрицы, можно судить о том, что в матрице не будет содержаться двух одинаковых или нулевых строк, а значит, её определитель не будет равен нулю.

Например,

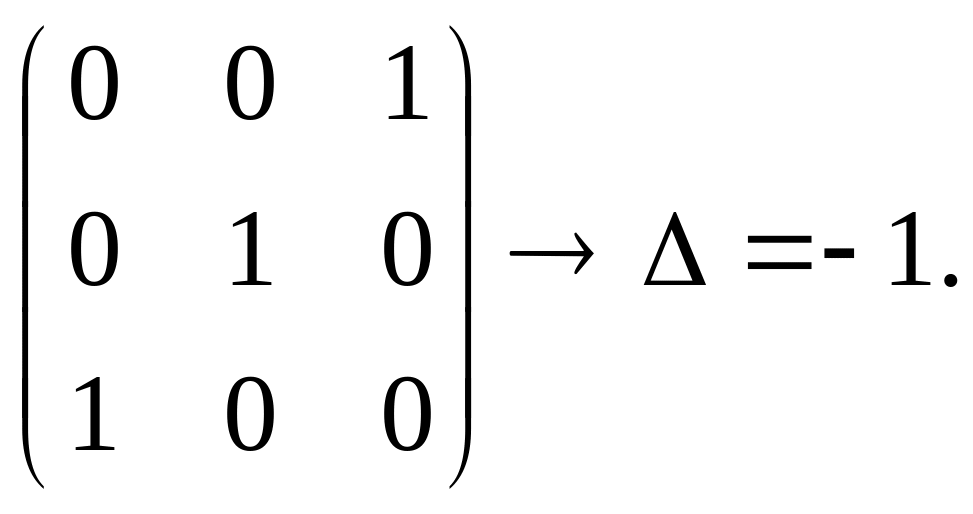
№3.

Вопрос по кривой порядка.

Кривой второго порядка называется множество всех точек комплексной плоскости, координаты которых удовлетворяют алгебраическому уравнению алгебраическому уравнению второй степени

a₁₁x² + 2a₁₂xy + a₂₂y² + 2a₁₀x + 2a₁₀y + a₀₀=0,

где коэффициенты a_ij (i,j= 0,1,2) – дейтвительные числа, причем a_11, a_12, a₂₂ не равны нулю одновременно и имеет место симметричность aij=aji.

В 17