
- •Поняття трансформації в економіці
- •Трансформаційні особливості економіки
- •Концепції управління перехідною економікою
- •Складання диференціального рівняння системи за її структурною схемою.
- •З'єднання ланок із зворотним зв'язком в одновимірній економічній системі.
- •Аналіз вихідних характеристик одновимірних економічних систем
- •Принцип суперпозиції для лінійних систем(вільні і вимушені рухи).
- •Способи знаходження перехідної матриці в багатовимірнихз системах
- •Знаходження перехідної матриці за теоремою розкладання Сильвестра
- •Аналіз стійкості економічних систем
Способи знаходження перехідної матриці в багатовимірнихз системах
Для
знаходження перехідної матриці
![]() використовують
3 способи :
використовують
3 способи :
метод варіації довільних сталих.
Якщо фундаментальна матриця
,
стовпці якої
утв.фундаментальну систему рішень одномірної системи диф.
рівняння , відома, то перехідна матриця знах.
за формулою![]() =
=
2)за теоремою розкладання Сильвестра. Перехідна матриця стаціонарної системи визначається за формулою:
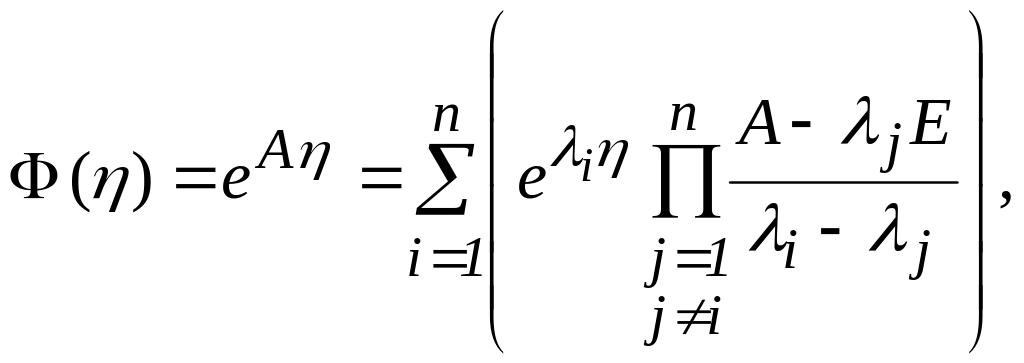
Де
![]() -
власні значення
матриці А
(тут передбачається, що вони різні),
а Е -
одинична матриця.
-
власні значення
матриці А
(тут передбачається, що вони різні),
а Е -
одинична матриця.
3)за
теоремою Келі-Гамільтона.
Розглянемо два випадки її
застосування.
1. У разі різних
власних значень матриці А:
![]() де n -
число рядків матриці А;
де n -
число рядків матриці А;
![]() -
(n-1)-й ступінь матриці А; коефіцієнти
-
(n-1)-й ступінь матриці А; коефіцієнти
![]() знаходяться із системи рівнянь
знаходяться із системи рівнянь
![]() 2. У
разі кратних власних значень матриці А формула
також справедлива.Корню
кратності m в системі n рівнянь
відповідають співвідношення
2. У
разі кратних власних значень матриці А формула
також справедлива.Корню
кратності m в системі n рівнянь
відповідають співвідношення
![]()
Знаходження перехідної матриці методом варіації довільних сталих Якщо фундаментальна матриця , стовпці якої утв.фундаментальну систему рішень одномірної системи диф. рівняння , відома, то перехідна матриця знах. за формулою =
Загальне рішення однорідної системи можна записати у вигляді де - довільні постійні.
Для стационарных систем следует выполнить действия:
Знайти корені ХР
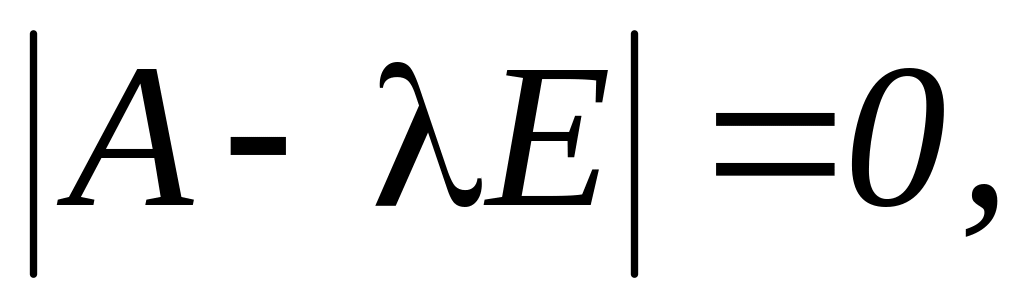 де Е
– одинична
матриця.
де Е
– одинична
матриця.
2. Выписать выражение общего решения для каждой компоненты вектора x, следуя известным правилам в зависимости от типа корней. При этом произвольные постоянные в выражении различны.
3. Полученные выражения подставить в однородную систему.
4. Приравнять коэффициенты при одинаковых функциях аргумента t и решить полученную систему уравнений.
5. Выписать общее решение, зависящее от n произвольных постоянных в форме . В результате находится фундаментальная матрица, а по формуле – переходная.
Знаходження перехідної матриці за теоремою розкладання Сильвестра
Перехідна матриця стаціонарної системи визначається за формулою:
Де - власні значення матриці А (тут передбачається, що вони різні), а Е - одинична матриця.Приклад:
![]()
![]()
А![]() Тоді
Тоді
![]() .
.
![]()
![]()
Знаходження перехідної матриці з використанням теореми Келі-Гамільтона Розглянемо два випадки її застосування. 1. У разі різних власних значень матриці А: де n - число рядків матриці А; - (n-1)-й ступінь матриці А; коефіцієнти знаходяться із системи рівнянь 2. У разі кратних власних значень матриці А формула також справедлива.Корню кратності m в системі n рівнянь відповідають співвідношення
Аналіз стійкості економічних систем
Економічна
система — це сукупність усіх видів
економічної діяльності людей у процесі
їх взаємодії. Система називається
стійкою,
якщо вона стійка за входом і за початковими
даними. Вигляд ДР:
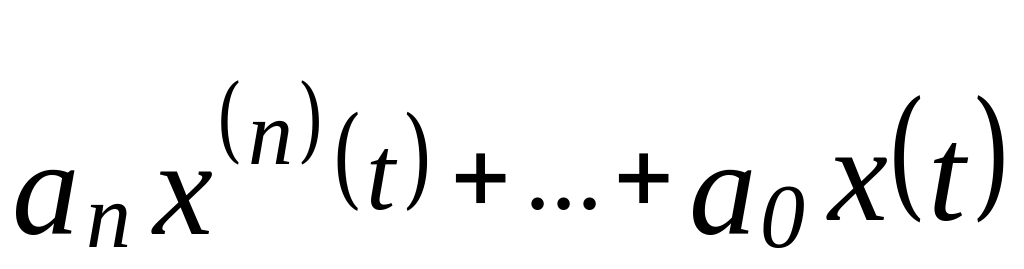 =
=
![]() .
.
Система
називається стійкою
за початковими даними,
якщо за ненульових обмежених поч. умов
віл. рух
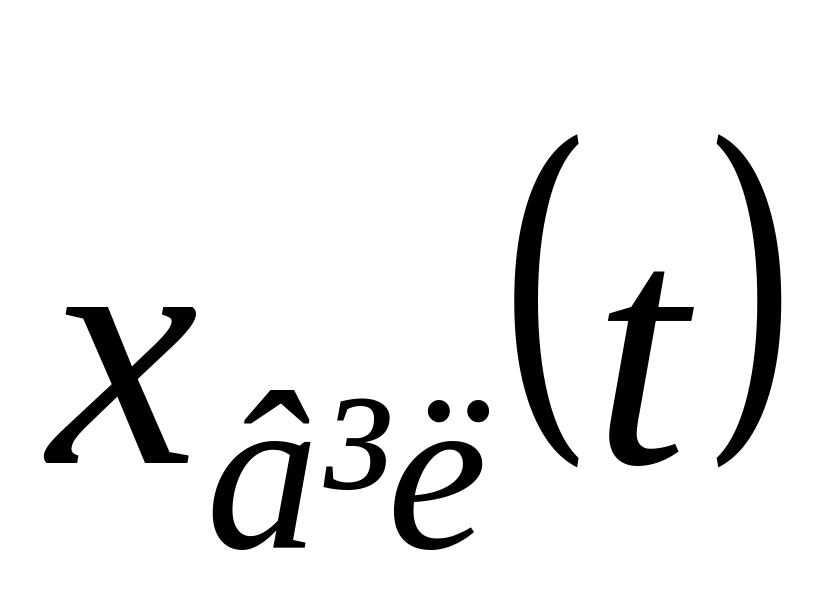 обмежений
при всіх
t
обмежений
при всіх
t![]() і
і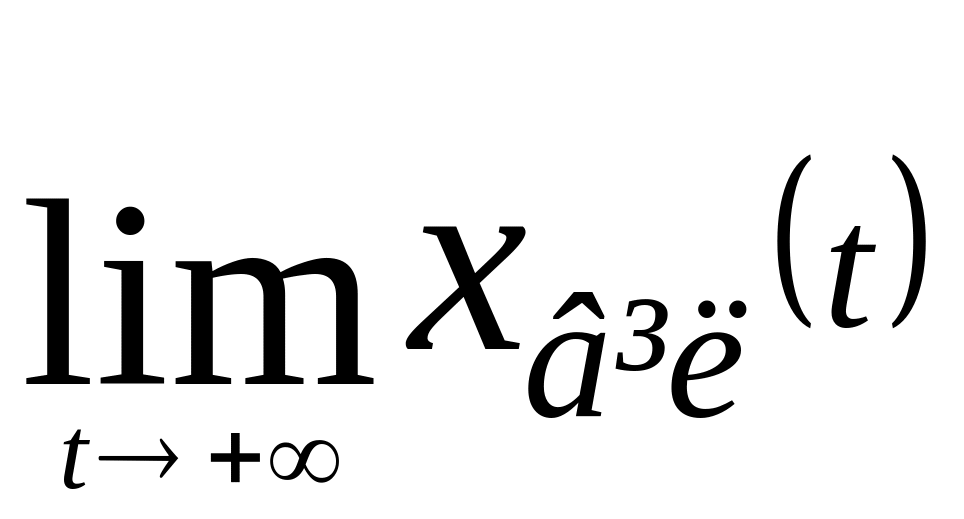 =0.
=0.
Система
називається стійкою
за входом,
якщо при будь-якій обмеженій дії
![]() реакція
системи
реакція
системи![]() є обмеженою у будь-який момент часу
t
є обмеженою у будь-який момент часу
t
![]() .
.
Критерії стійкості: 1)стійка за поч. даними; 2) критерій Рауса-Гурвіца; 3)стійка за входом.
Необхідна умова стійкості: якщо система стійка, то всі коефіцієнти характеристичного рівняння додатні.
Приклад:
![]() =
g
Характеристичне
рівняння
=
g
Характеристичне
рівняння
![]() має
від’ємні(кратні) корені
має
від’ємні(кратні) корені![]() =
- 1,
ао=1>0,
система
стійка. Порядок
(m
= 0) правої
частини
рівняння меньше
порядка (n
= 2) лівої
частини
- m<n
– система
стійка за входом. Згідно 1) і 3) критеріям
система стійка.
=
- 1,
ао=1>0,
система
стійка. Порядок
(m
= 0) правої
частини
рівняння меньше
порядка (n
= 2) лівої
частини
- m<n
– система
стійка за входом. Згідно 1) і 3) критеріям
система стійка.
Стійкість економічних систем за початковими даними
Економічна система — це сукупність усіх видів економічної діяльності людей у процесі їх взаємодії.
Система називається стійкою за початковими даними, якщо за ненульових обмежених поч. умов віл. рух обмежений при всіх t і =0.
Критерій
стійкості : Для
стійкості системи за поч. даними необхідно
і достатньо, щоб корені
![]() характеристичного
рівняння
характеристичного
рівняння
![]() =
0
мали від’ємні дійсні частини : Re
< 0, i
=
1,…, n
знаходились в лівій півплоскості
комплексної плоскості.
=
0
мали від’ємні дійсні частини : Re
< 0, i
=
1,…, n
знаходились в лівій півплоскості
комплексної плоскості.
Приклад: = g Характеристичне рівняння має від’ємні(кратні) корені = - 1, ао=1>0, система стійка за початковими даними.
Стійкість економічних систем за входом
Економічна система — це сукупність усіх видів економічної діяльності людей у процесі їх взаємодії.
Система називається стійкою за входом, якщо при будь-якій обмеженій дії реакція системи є обмеженою у будь-який момент часу t .
Критерій
стійкості :
Якщо с-ма стійка за поч. даними і порядок
m
диференціального
оператора M(p)=![]() +…+
+…+![]() правої
частини
рівняння
не більше порядку n
і диференціального оператора D(p)=
правої
частини
рівняння
не більше порядку n
і диференціального оператора D(p)=![]() +…+
+…+![]() лівої
частини, тобто
m
лівої
частини, тобто
m![]() n,
то система стійка
за входом.
n,
то система стійка
за входом.
Приклад: = g. Порядок (m = 0) правої частини рівняння меньше порядка (n = 2) лівої частини - m<n – система стійка за входом.
Прямий і побічний критерії стійкості економічних систем
Перший критерій стійкості(за початковими даними) називається прямим, а другий(критерій Рауса-Гурвіца) – побічним, тому що в цьому випадку процедура аналізу стійкості не вимагає знаходження коренів рівняння.
Для стійкості системи за поч. даними необхідно і достатньо, щоб корені характеристичного рівняння = 0 мали від’ємні дійсні частини : Re < 0, i = 1,…, n знаходились в лівій півплоскості комплексної плоскості.
Критерій Рауса-Гурвіца - для стійкості системи за поч. даними необхідно і достатньо, щоб кутові мінори
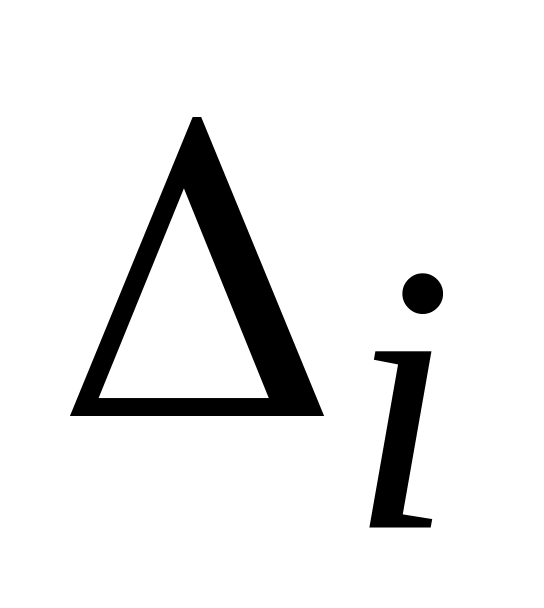 матриці
були додатніми
>0,
i=1,…,n,
де
матриці
були додатніми
>0,
i=1,…,n,
де
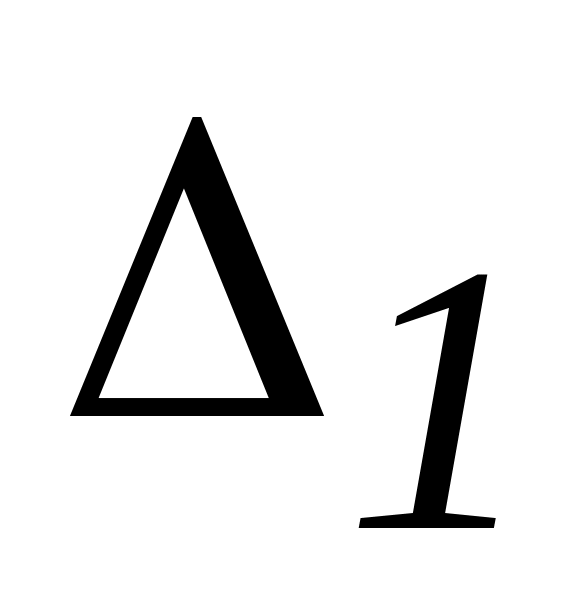 =
=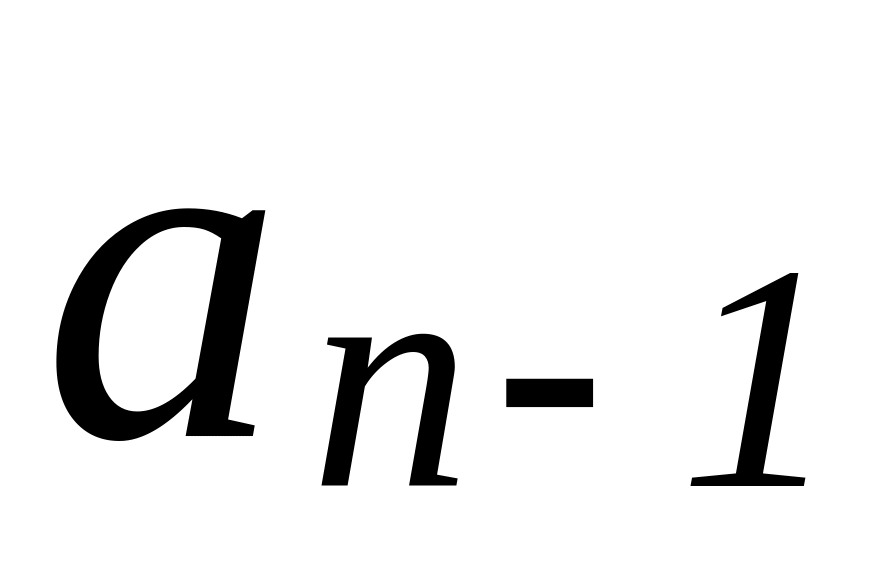 ,
,
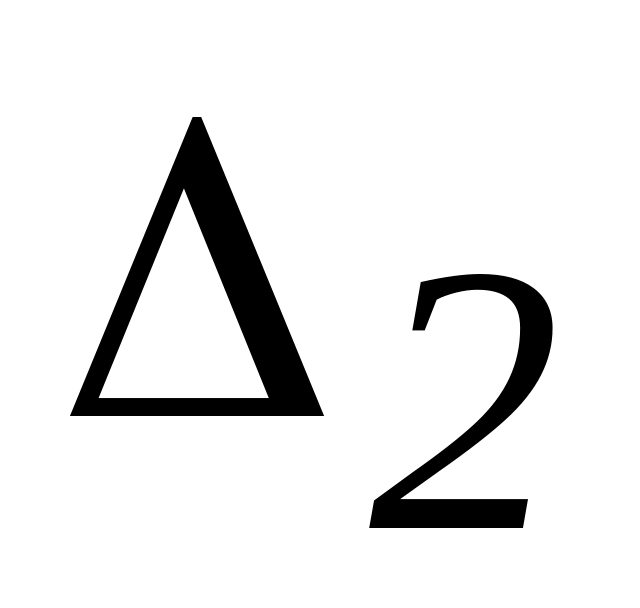 =
=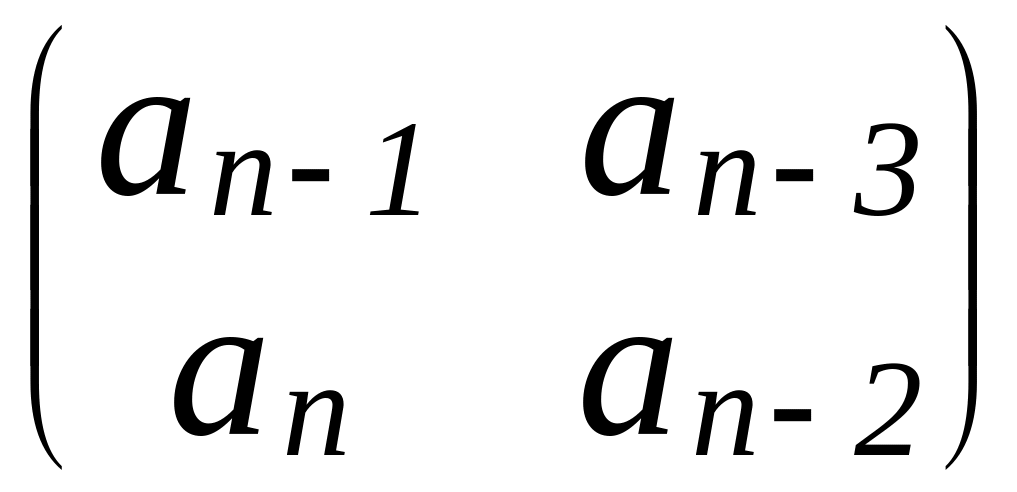 …
…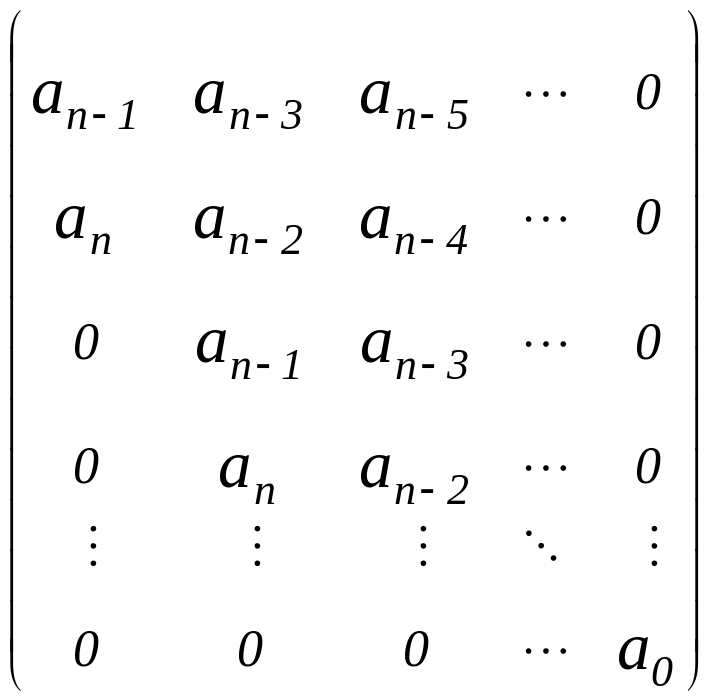
Приклад: = g Характеристичне рівняння має від’ємні(кратні) корені = - 1, ао=1>0, система стійка за початковими даними.
Критерій Рауса-Гурвіца
Економічна
система — це сукупність усіх видів
економічної діяльності людей у процесі
їх взаємодії. Критерій
Рауса-Гурвіца(використовується
для перевірки від’ємних дійсних частин
коренів характеристичного рівняння) –
для стійкості системи за поч. даними
необхідно і достатньо, щоб кутові
мінори
матриці
були додатніми
>0,
i=1,…,n,
де
=
,
=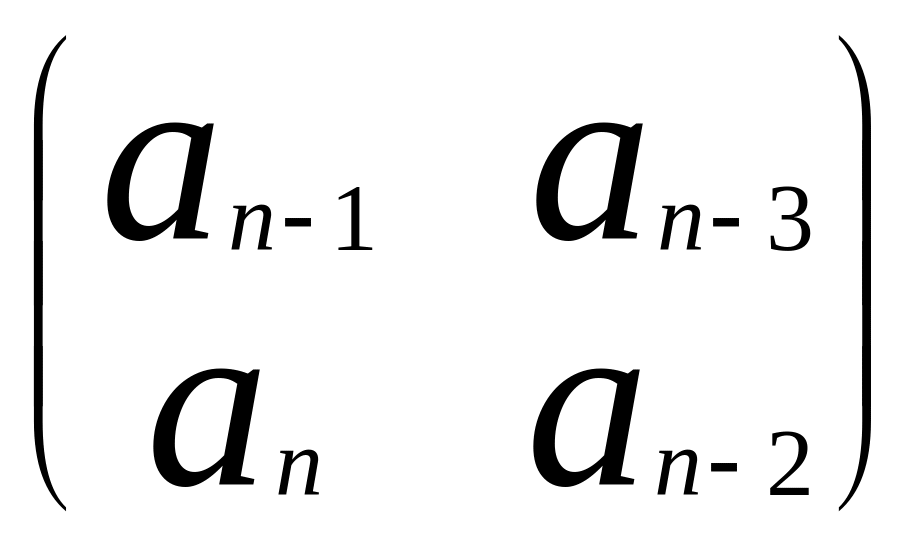 …
…
При
заповненні матриці відсутні в рівнянні
коефіцієнти![]() і
і
![]() при і >n
заміняються 0.
при і >n
заміняються 0.
Приклад:
![]() =
g.
=
g.
![]() =
1,
=
1,
![]() =
2,
=
2,
![]() =
3,
=
3,
![]() =
4.
=
4.
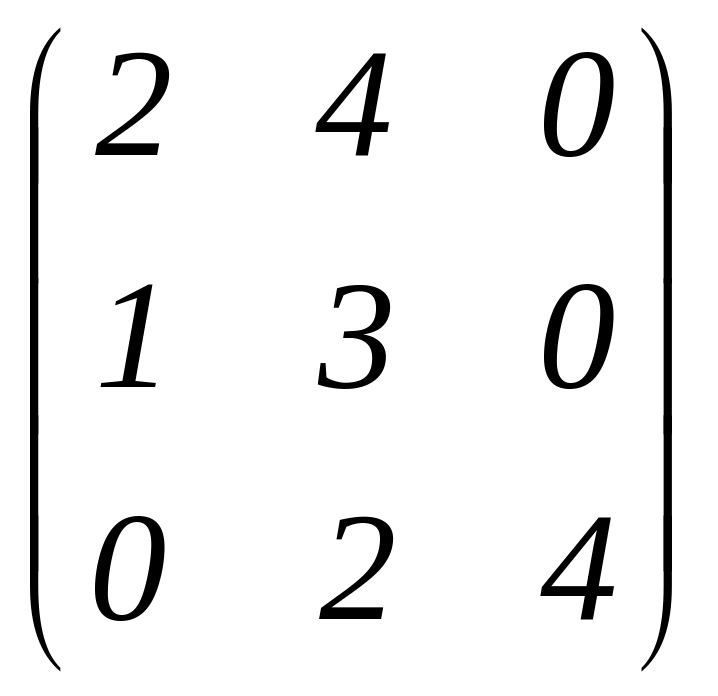
Розраховуємо
кутові мінори:
![]() =
2 > 0,
=
=
2 > 0,
=![]() =2
> 0,
=2
> 0,
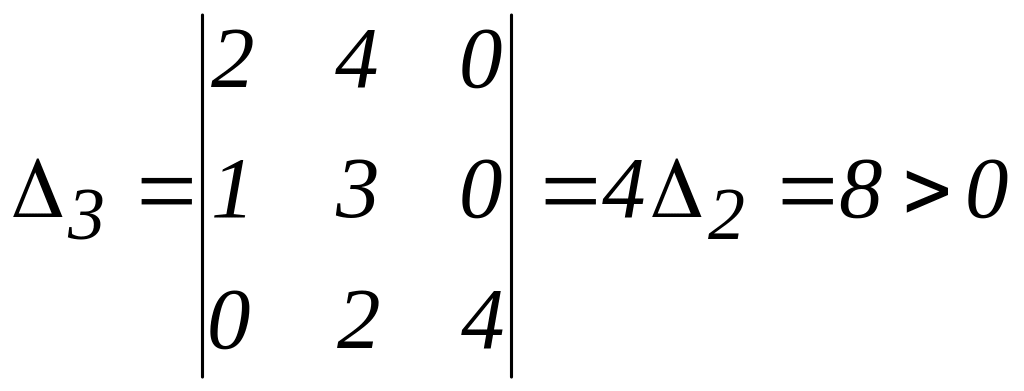 .Вони
додатні. Згідно критерію
Рауса-Гурвіца
с-ма стійка.
.Вони
додатні. Згідно критерію
Рауса-Гурвіца
с-ма стійка.
Стійкість багатовимірних економічних систем
Розглядається
лінійна багатовимірна стаціонарна
система
![]()
![]() ,
Багатовимірна система називається
асимптотично стійкою, якщо її вільний
рух
обмежений при початкових станах
,
Багатовимірна система називається
асимптотично стійкою, якщо її вільний
рух
обмежений при початкових станах
![]() і виконується умова
і виконується умова
![]()
Приклад:
![]()
![]() Тоді
Тоді![]() Характеристичне рівняння
Характеристичне рівняння
![]() або
або
![]() має від’ємні корені:
має від’ємні корені:
![]() Згідно в першим критерієм(
Згідно в першим критерієм(![]() )
система стійка.
)
система стійка.
Необхідна умова стійкості економічних систем
Необхідна умова стійкості: якщо система(для багатовимірних с-м – асимптотично) стійка, то всі коефіцієнти характеристичного рівняння додатні.
Приклад одновимірної: = g Характеристичне рівняння має від’ємні(кратні) корені = - 1, ао=1>0, система стійка. Порядок (m = 0) правої частини рівняння меньше порядка (n = 2) лівої частини - m<n – система стійка за входом. Згідно 1) і 3) критеріям система стійка.
Приклад
багатовимірної:
Тоді
Характеристичне рівняння
або
має від’ємні корені:
![]() Згідно в першим критерієм(
Згідно в першим критерієм(![]() )
система стійка.
)
система стійка.
Достатні критерії стійкості економічних систем
Критерії стійкості багатовимірних систем:
Для асимптотичної стійкості системи необхідно і достатньо, щоб корені
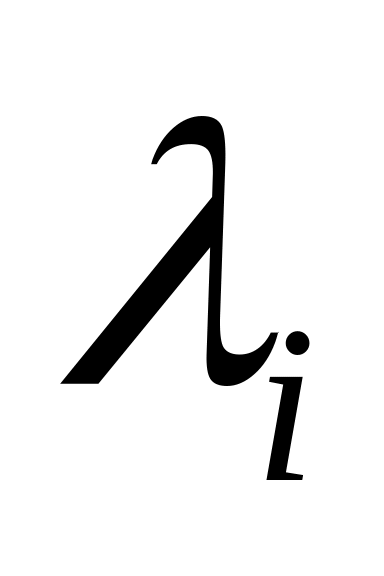 характеристичного
рівняння det
характеристичного
рівняння det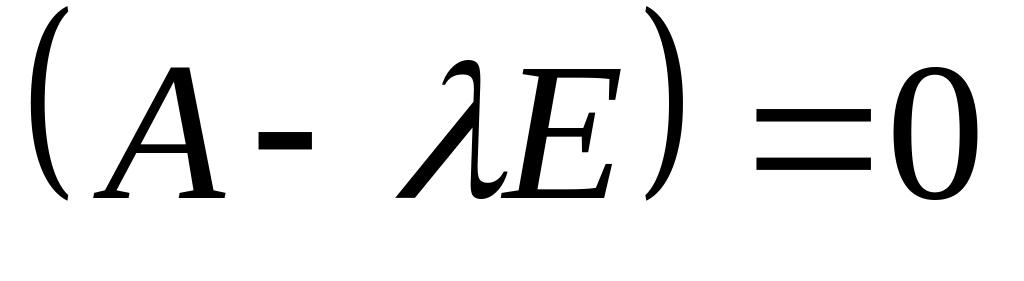 мали від’ємні дійсні частини: Re
,
мали від’ємні дійсні частини: Re
,
 ,…,n,
тобто знаходились в лівій півплоскості
комплексної плоскості.
,…,n,
тобто знаходились в лівій півплоскості
комплексної плоскості.Критерій Рауса-Гурвіца(використовується для перевірки від’ємних дійсних частин коренів характеристичного рівняння).
Приклад: Тоді Характеристичне рівняння або має від’ємні корені: Згідно в першим критерієм( ) система стійка.
Аналіз керованості та спостережуваності систем
Нехай
дана багатовимірна система, що описує
рівняння стану і виходу з відповідними
матрицями А, В, С -
![]()
![]()
![]()
Система називається керованою, якщо вибором деякого керуючого впливу її можна перевезти з довільного початкового стану у довільний наперед заданий кінцевий стан.
Система називається спостережуваною, якщо за реакцією на виході системи при заданому керуючому впливі можна визначити початковий стан системи.
Алгоритм рішення : 1) в рівняннях стану та виходу виділимо матриці А, В, С; 2) зіставимо матрицю керованості W та матрицю спостережуваності Q; 3) підрахувати ранги обох матриць и зробити висновок про керованість та спостережуваність на основі кожного критерію.
Приклад: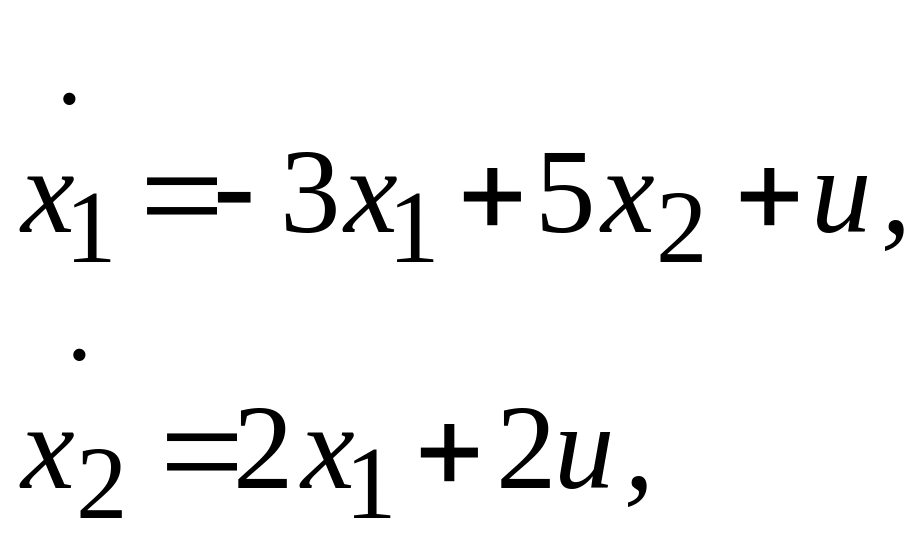
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (B
AB)
(B
AB)![]()
![]()
![]() (
(![]()
![]() )
)![]() Згідно
з критеріями система є керованою, але
не являється повністю спостережуваною.
Згідно
з критеріями система є керованою, але
не являється повністю спостережуваною.
Критерій керованості трансформаційних систем
Для
того, щоб система була керованою
необхідно і достатньо, щоб ранг матриці
керованості
(![]()
![]()
![]() …
…
![]() )
дорівнював вимірності вектора стану
)
дорівнював вимірності вектора стану
![]() .
.
Алгоритм рішення : 1) в рівняннях стану та виходу виділимо матриці А, В, С; 2) зіставимо матрицю керованості W та матрицю спостережуваності Q; 3) підрахувати ранги обох матриць и зробити висновок про керованість та спостережуваність на основі кожного критерію.
Приклад:
(B AB) Згідно з критерієм система є керованою.
Критерій спостережуваності трансформаційних сисі достатем
Для
того, щоб система була достатньо
спостережуваною,
необхідно і достатньо, щоб ранг матриці
спостережуваності Q=(
![]() …
…
![]() )
дорівнював вимірності вектора стану
)
дорівнював вимірності вектора стану
![]() .
.
Алгоритм рішення : 1) в рівняннях стану та виходу виділимо матриці А, В, С; 2) зіставимо матрицю керованості W та матрицю спостережуваності Q; 3) підрахувати ранги обох матриць и зробити висновок про керованість та спостережуваність на основі кожного критерію.
Приклад: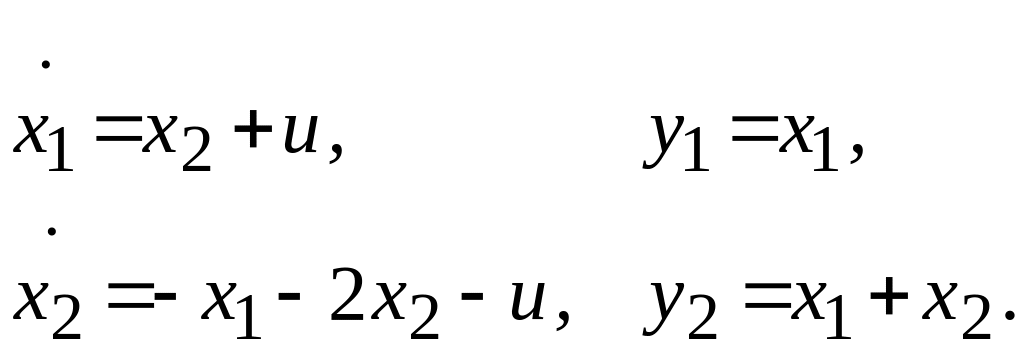
![]()
![]()
![]()
![]()
(
)![]()
![]() Згідно з критерієм система є
спостережуваною..
Згідно з критерієм система є
спостережуваною..
