Содержание

1 Оптимизация грузопотоков 4

2 Маршрутизация перевозок 19

3 Выбор подвижного состава 26

Литература

1 Оптимизация грузопотоков

В решении задач, направленных на дальнейшее совершенствование работы автомобильного транспорта и повышение эффективности использования транспортных средств, экономное использование трудовых, финансовых и материальных ресурсов, рост производительности труда и снижение себестоимости перевозок, важная роль отводится применению современных экономико-математических методов и электронно-вычислительной техники (ЭВМ).

Одним из основных резервов снижения транспортных издержек является достижение наименьшего расстояния перевозок грузов путем рационального закрепления получателей за поставщиками (оптимизация грузопотоков).

Цель работы - освоить методику решения заданной транспортной задачи с помощью экономико-математических методов.

Постановка транспортной задачи

Задача оптимизации грузопотоков - это определение плана перевозок однородных (взаимозаменяемых) грузов от m поставщиков А_i к n потребителям B_j с учетом ограничений на ресурсы и потребности, обеспечивающие минимальную транспортную работу.

Если обозначить объем вывоза груза от поставщиков А_i через Q_i , требуемый объем завоза груза потребителю B_j через Q_j, перевозимое количество груза от i-го поставщика j-му потребителю Q_ij, кратчайшее расстояние перевозки от i -го поставщика до j -го потребителя через l_ij, то задачу оптимизации грузопотоков можно выразить в следующей математической форме:

• во все j-e пункты получения груза из i-ro пункта отправления может быть вывезено только Q_j единиц груза

=Q_i, i = 1,2…,m ; (1.1)

• из всех i - х пунктов отправления j-му пункту получения должно быть доставлено только Q_j единиц груза

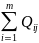=Q_j, j = 1,2…,n. (1.2)

При этом общий объем транспортной работы перевозок должен быть минимальным, что соответствует достижению наименьшего среднего расстояния перевозок

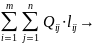min , (1.3)

а искомые переменные не могут быть отрицательными числами, т.е.

Q_ij ≥ 0. (1.4)

Если общий объем вывоза грузов от поставщиков равен общему объему их завоза потребителям, то имеет место условие

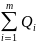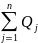= . (1.5)

Ограничения (1.1),(1.2),(1.4),(1.5) и целевая функция (1.3) являются закрытой моделью классической задачи линейного программирования.

Для оценки первоначального базисного и отыскания оптимального плана закрепления потребителей груза за поставщиками как задачи линейного протраммирования используются следующие методы: квадратов, опорных элементов, распределительные (Хичкока, Креко, модифицированный, распределительный метод — МОДИ), с разрешающими элементами[1,2].

Широкое применение получил метод МОДИ, который называют еще методом потенциалов.

Для решения поставленной транспортной задачи предлагается использовать данный метод.

Метод потенциалов

Рассмотрим решение транспортной задачи этим методом на примере.

Условия задачи. Имеется несколько поставщиков и получателей однородной или взаимозаменяемой продукции. Известны наличие груза у каждого поставщика и потребность в нем у каждого получателя, а также расстояния между ними (таблицы 1.1,1.2,1.3).

Таблица 1.1 - Наличие груза у поставщиков

Индекс поставщика	Наличие груза, т
А1	360
А2	180
А3	135
Итого:	675

Таблица 1.2 - Потребность в грузе у получателей

Индекс получателя	Потребность в грузе, т
Б1	135
Б2	135
Б3	225
Б4	180
Итого:	675

Необходимо составить оптимальный план закрепления получателей за поставщиками, при котором общая стоимость доставки груза была бы минимальной.

В соответствии с «Прейскурантом № 13-01-02 единых тарифов на перевозку грузов автомобильным транспортом» стоимость перевозки зависит от класса груза и расстояния доставки. Согласно условию, груз является однотипным, т. е. имеет одинаковый класс, и поэтому стоимость перевозки будет зависеть только от расстояния.

Следовательно, задача на отыскание оптимального варианта закрепления получателей за поставщиками сводится к отысканию минимального среднего расстояния перевозки грузов.

Для получения оптимального плана закрепления получателей за поставщиками задачу решаем методом последовательного улучшения вариантов.

Таблица 1.3 - Расстояние от поставщиков до получателей, км

Получатели	Поставщики
	А1	А2	А3
Б1	20	6	12
Б2	32	16	16
Б3	22	18	0
Б4	32	14	30

Исходные данные задачи сводим в матрицу №1, представляющую собой таблицу, в которой по строкам располагаем сведения о потребителях груза, а по столбцам - о поставщиках. В верхнем правом углу каждой клетки матрицы - в квадрате - проставляем расстояние от поставщиков к потребителям.

Получатели	Вспомогательные коэффициенты	Поставщики									Потребность в грузе, т
		А1			А2			А3
Б1				20			6			12		135
Б2				32			16			16		135
Б3				22			18			0		225
Б4				32			14			30		180
Наличие груза, т			360			180			135			675

Рисунок 1.1 - Матрица №1. Исходный план перевозок

Матрица с проставленными в ней исходными данными показана на рисунке 1.1 и называется исходным планом перевозок.

Математически транспортная задача линейного программирования формулируется следующим образом. Обозначим количество груза буквой х с двумя индексами: первый показывает, откуда везут, а второй - куда доставляют груз.

Первая группа уравнений - по поставщикам

x₁₁+ x₁₂+ x₁₃+ x₁₄ = 360;

x₂₁+ x₂₂+ x₂₃+ x₂₄ = 135; (1.6)

x₃₁+ x₃₂+ x₃₃+ x₃₄ = 180.

Вторая группа показывает ограничение количества груза по получателям

x₁₁+ x₂₁+ x₃₁ = 135;

x₁₂+ x₂₂+ x₃₂ = 135; (1.7)

x₁₃+ x₂₃+ x₃₃ =225;

x₁₄+ x₂₄+ x₃₄ =180.

Общее уравнение для отыскания минимального среднего расстояния перевозки

C_min =20x₁₁+6x₂₁+12x₃₁+32x₁₂+16x₂₂+16x₃₂ +22x₁₃+18x₂₃+0x₃₃+ +32x₁₄+14x₂₄+30x₃₄. (1.8)

Приведенное уравнение является линейным, так как содержит неизвестные только в первой степени. Согласно условию и смыслу, значение может быть только положительным.

Решение задачи с таким количеством неизвестных представляет значительные трудности, поскольку дает большое число их возможных значений. Подобные задачи лучше всего решать методом последовательного улучшения вариантов закрепления получателей за поставщиками.

Согласно заданию составляем первичный план закрепления получателей за поставщиками

Получа- тели		Вспомогательные коэффициенты	Поставщики													Потребность в грузе, т
			А1				А2						А3
Б1			135		20					6				12		135
Б2					32					16		135		16		135
Б3				225		22			18						0	225
Б4						32		180	14						30	180
Наличие груза, т				360				180			135						675

Рисунок 1.2 - Матрица №2. Первичный план закрепления получателей за поставщиками

Клетки матрицы, в которых поставлены цифры загрузки, называются загруженными (клетки А1БЗ, А1Б1,АЗБ2, А2Б4). Остальные клетки, не имеющие загрузки, называются незагруженными.

Решение задачи возможно при соблюдении некоторых правил.

Правило 1. Число загруженных клеток в матрице должно быть равно m+n-1 (m, n - число строк и столбцов).

В нашем примере m = 4, n = 3, следовательно, m+n -1=4+3 - 1=6. На матрице число загруженных клеток равно 6.

Если число загруженных клеток больше m+n - 1, то план закрепления получателей за поставщиками составлен неверно, и задачу решить нельзя. Нужно составить новый план закрепления, соблюдая приведенное выше правило. Если число загруженных клеток меньше m+n - 1, то задачу решить можно, загружая недостающее число клеток нулевой загрузкой (фиктивная загрузка). Для этого в одну или несколько клеток проставляют ноль.

Правило 2. Нулевую загрузку проставляют в клетках столбца с наи­меньшим количеством груза и с минимальным расстоянием.

Матрица с нулевой загрузкой (№3) приведена на рисунке 1.3.

Получа- тели	Вспомога- тельные коэффициенты	Поставщики						Потребность в грузе, т
		А1		А2		А3
Б1		135	20		6		12		135
Б2		0	32	0	16	135	16		135
Б3		225	22		18		0		225
Б4			32	180	14		30		180
Наличие груза, т		360		180		135			675

Рисунок 1.3 - Матрица №3. Введение фиктивной (нулевой) загрузки.

Следующим этапом является отыскание вспомогательных коэффициентов строки и столбца, руководствуясь следующим правилом-

Правило 3. Сумма вспомогательных коэффициентов строки и столбца должна равняться расстоянию, проставленному в загруженной клетке.

Матрица №4 с поставленными на ней вспомогательными коэффициентами показана на рисунке 1.4.

Получа- тели	Вспомога- тельные коэффициенты	Поставщики						Потребность в грузе, т
		А1		А2		А3
		20		4		4
Б1	0	135	20		6		12		135
Б2	12	0	32	0	16	135	16		135
Б3	2	225	22		18		0		225
Б4	10		32	180	14		30		180
Наличие груза, т		360		180		135			675

Рисунок 1.4 - Матрица №4 со вспомогательными коэффициентами

После отыскания вспомогательных коэффициентов проверяем матрицу на потенциальность.

Правило 4. Потенциальной называется незагруженная клетка, у которой сумма вспомогательных коэффициентов строки и столбца больше проставленного в ней расстояния.

Матрица №5 с проставленными потенциалами показана на рисунке 1.5.

Получа- тели	Вспомога- тельные коэффициенты	Поставщики						Потребность в грузе, т
		А1		А2		А3
		20		4		4
Б1	0	135	20		6		12		135
Б2	12	0	32	0	16	135	16		135
Б3	2	225	22		18	6	0		225
Б4	10		32	180	14		30		180
Наличие груза, т		360		180		135			675

Рисунок 1.5 - Матрица №5 с обозначенными величинами потенциалов Наличие потенциальных клеток в матрице свидетельствует о том, что составленный вариант закрепления получателей за поставщиками не является оптимальным и может быть улучшен. Улучшение варианта закрепления получателей за поставщиками производится при помощи контура.

Правило 5. Контур представляет собой замкнутую ломаную линию, состоящую из попеременных отрезков вертикальных и горизонтальных прямых, вершины которых находятся в загруженных клетках; началом контура является клетка с наибольшим по величине потенциалом; отрезки контура должны проходить через возможно большее число загруженных клеток, но не менее двух, считая и потенциальную; линии контура должны замкнуться в потенциальной клетке, из которой контур взял свое начало; вершины перегиба линий контура должны лежать только в загруженных клетках и угол перегиба должен быть прямым, т.е. составлять 90°. Вершины перегибов линий контура обозначаются попеременно знаками плюс и минус, причем первый минус ставится в потенциальной клетке.

В каждой матрице из данной потенциальной клетки можно провести только один контур.

На матрице №6 показаны линии контура для данного случая. Образцы возможных линий контура при решении транспортных задач приведены на рисунке 1.6.

Получа- тели	Вспомога- тельные коэффициенты	Поставщики						Потребность в грузе, т
		А1		А2		А3
		20		4		4
Б1	0	135	20		6		12		135
Б2	12	0	32	0	16	135	16		135
			-				+
Б3	2	225	22		18	6	0		225
			+				-
Б4	10		32	180	14		30		180
Наличие груза, т		360		180		135			675

Рисунок 1.6 – Матрица №6 с линиями контура

Следующим этапом решения задачи является отыскание минимального числового значения загрузки в клетках, где вершины контура имеют знак плюс.

Новый план закрепления получателей за поставщиками показан на матрице №7 (рисунок 1.7).

Получа- тели	Вспомога- тельные коэффициенты	Поставщики						Потребность в грузе, т
		А1		А2		А3
		20		4		4
Б1	0	135	20		6		12		135
Б2	12	135	32		16		16		135
Б3	2	90	22		18	135	0		225
Б4	10		32	180	14		30		180
Наличие груза, т		360		180		135			675

Рисунок 1.7 - Матрица №7. Улучшенный вариант закрепления потребителей за поставщиками

В результате проведенных действий произошло следующее:

- при переносе 135 единиц из клетки АЗБ2 в клетку АЗБ3 расстояние перевозки уменьшилось на 16 км (16 – 0 = 16);

• при переносе цифры 135 из клетки А1Б3 в клетку А1Б2 расстояние увеличилось на 10 км (32 - 22 = 10);

Таким образом, общее уменьшение расстояния перевозки 135 единиц груза составило 16- 10= 6 км, т.е. оно численно равно величине потенциала потенциальной клетки, из которой контур взял свое начало.

В связи с тем, что уменьшение расстояния перевозок численно равно потенциалу, контур следует начинать из клетки с наибольшим значением потенциала.

Продолжаем исследование матрицы № 7. Проверяем ее на число загруженных клеток. Оно равно 5, т.е. не соответствует правилу, при котором число загруженных клеток должно быть равно 4 + 3-1= 6.

В связи с тем, что число загруженных клеток на единицу меньше необходимого, вводим нулевую загрузку в клетку А1Б4. Находим вспомогательные коэффициенты строки и столбца, проставляем их в матрицу и проверяем ее на потенциальность. В матрице №8 нет потенциальных клеток, что свидетельствует о получении оптимального плана закрепления получателей за поставщиками:

Получа- тели	Вспомога- тельные коэффициенты	Поставщики						Потребность в грузе, т
		А1		А2		А3
		20		2		-2
Б1	0	135	20		6		12		135
Б2	12	135	32		16		16		135
Б3	2	90	22		18	135	0		225
Б4	12	0	32	180	14		30		180
Наличие груза, т		360		180		135			675

Рисунок 1.8 - Матрица №8. Оптимальный план перевозок

Расшифрованный оптимальный план перевозок передают в диспетчерскую для определения дневных заданий шоферам и выписки путевых листов.

Рассмотрим итоги решения задачи на закрепление получателей за поставщиками.

Среднее расстояние перевозки груза определяется из выражения

l_пер = , (1.9)

где Q_i, - количество перевозимого груза, указанного в клетке рассматриваемой матрицы, т;

l_i – расстояние между поставщиком и получателем, соответствующее грузу Q, км.

Тогда при первичном плане закрепления получателей за поставщиками среднее расстояние перевозки

l′_пер = 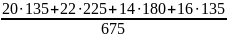= 18,27 км,

при оптимальном плане

l″_пер = 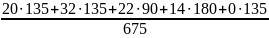= 17,07 км.

Уменьшение среднего расстояния перевозки в процентах определится по формуле

Δl = 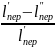, (1.10)

где l′_пер и l″_пер – среднее расстояние перевозки, соответственно, при первичном и улучшенном плане закрепления получателей за поставщиками, км.

Тогда уменьшение среднего расстояния перевозки при оптимальном плане по отношению к первичному

Δl = 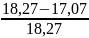∙100 % = 6,57 %.

Таким образом, каждый последующий вариант закрепления получателей за поставщиками дает все меньшие значения уменьшения среднего расстояния перевозки и поэтому при решении сложных и громоздких задач можно не добиваться оптимального варианта, а ограничиться двумя-тремя вариантами улучшения плана.