Свойства определителей:

1. Если квадратная матрица A^T является транспонированной матрицей A, то их определители совпадают |A^T | = |A|, т.е. определитель не меняется, если заменить его строки столбцами и обратно, например, для определителя третьего порядка .

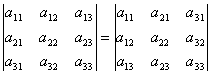2. При перестановке 2-х строк или столбцов определитель изменит знак на противоположный, сохраняя абсолютную величину, т.е., например,

3. Если определитель имеет две одинаковые строки или столбца, то он равен нулю. Например, .

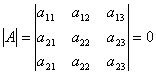4. Общий множитель строки или столбца можно выносить за знак определителя. Например, .

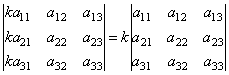5. Если все элементы какой–либо строки или столбца определителя равны нулю, то сам определитель равен нулю.

6. Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель можно представить в виде суммы 2-х определителей по формуле, например,

.

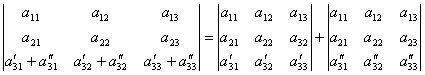7. Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель не изменит своей величины. Например,

.

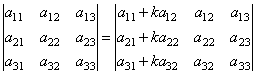Эти свойства определителей довольно часто используются при вычислении определителей и в различных задачах.

Пунтк 4. Алгебраические дополнения и миноры.

Пусть имеем определитель третьего порядка: .

Минором, соответствующим данному элементу a_ij определителя третьего порядка, называется определитель второго порядка, полученный из данного вычёркиванием строки и столбца, на пересечении которых стоит данный элемент, т.е. i-ой строки и j-го столбца. Миноры соответствующие данному элементу a_ij будем обозначать M_ij.

Например, минором M₁₂, соответствующим элементу a₁₂, будет определитель 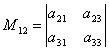, который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца.

Таким образом, формула, определяющая определитель третьего порядка, показывает, что этот определитель равен сумме произведений элементов 1-ой строки на соответствующие им миноры; при этом минор, соответствующий элементу a₁₂, берётся со знаком “–”, т.е. можно записать, что

.

(1)

Алгебраическим дополнением элемента a_ij определителя называется его минор M_ij, умноженный на

(–1)^i+j.

Алгебраическое дополнение элемента a_ij обозначается A_ij.

Из определения получаем, что связь между алгебраическим дополнением элемента и его минором выражается равенством A_ij = (–1)^i+jM_ij.

Например,

Пример 7. Дан определитель . Найти A₁₃, A₂₁, A₃₂.

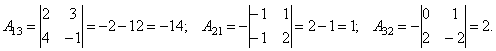
Легко видеть, что используя алгебраические дополнения элементов, формулу (1) можно записать в виде:

.

Аналогично этой формуле можно получить разложение определителя по элементам любой строки или столбца.

Например, разложение определителя по элементам 2-ой строки можно получить следующим образом. Согласно свойству 2 определителя имеем:

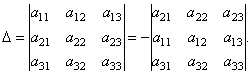
Разложим полученный определитель по элементам 1-ой строки.

.

(2)

Отсюда т.к. определители второго порядка в формуле (2) есть миноры элементов a₂₁, a₂₂, a₂₃. Таким образом, , т.е. мы получили разложение определителя по элементам 2-ой строки.

Аналогично можно получить разложение определителя по элементам третьей строки. Используя свойство 1 определителей (о транспонировании), можно показать, что аналогичные разложения справедливы и при разложении по элементам столбцов.

Таким образом, справедлива следующая теорема.

Теорема (о разложении определителя по заданной строке или столбцу). Определитель равен сумме произведений элементов какой–либо его строки (или столбца) на их алгебраические дополнения.

Всё вышесказанное справедливо и для определителей любого более высокого порядка.

Пример 8.

1. Вычислить определитель 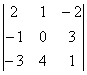, раскладывая его по элементам 2-го столбца.

2. Вычислить определитель, используя его свойства. Прежде чем раскладывать определитель по элементам какой–либо строки, сводя к определителям третьего порядка, преобразуем его, используя свойство 7, сделав в какой–либо строке или столбце все элементы, кроме одного, равными нулю. В данном случае удобно рассмотреть 4-й столбец или 4-ю строку:

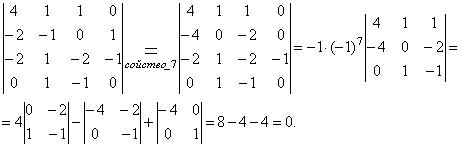
Пункт 5. Обратная матрица.

Понятие обратной матрицы вводится только для квадратных матриц.

Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A^-1 и удовлетворяющая условию , где Е – единичная матрица.

Справедлива следующая теорема:

Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.

Если условия теоремы выполнены, то матрица обратная к матрице находится следующим образом

,

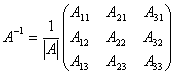где A_ij - алгебраические дополнения элементов a_ij данной матрицы A.

Итак, чтобы найти обратную матрицу нужно:

1. Найти определитель матрицы A.

2. Найти алгебраические дополнения A_ij всех элементов матрицы A и составить матрицу , элементами которой являются числа A_ij.

3. Найти матрицу, транспонированную полученной матрице , и умножить её на – это и будет .

Аналогично для матриц второго порядка, обратной будет следующая матрица .

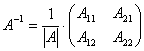Пример 9.

1. Найти матрицу, обратную данной 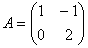. Сделать проверку.

|A| = 2. Найдем алгебраические дополнения элементов матрицы A.

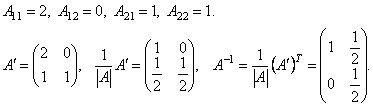
Проверка:

.

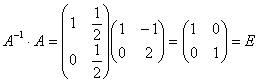Аналогично A∙A^-1 = E.

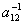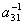2. Найти элементы и матрицы A^-1 обратной данной

.

Вычислим |A| = 4. Тогда .

.

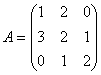3. . Найдем обратную матрицу.
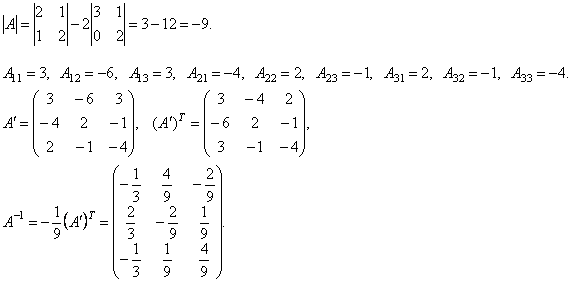