Модуль 4. Основы дискретной математики, теории вероятности и математической статистики. Тема 4.1. Множества и операции над ними.

1. Понятие множества.

2. Задание множества.

3. Операции над множествами.

Пункт 1. Понятие множества.

Понятие множества принадлежит к числу фундаментальных неопределяемых понятий. Можно сказать, что множество – это любая определенная совокупность объектов. Объекты, из которых составлено множество, называют элементами. Элементы множества отличают друг от друга. Например, множество всех книг в библиотеке или множество вершин многоугольника.

Множества обозначаются большими буквами. Например, A, B, C, X, N и т.д. Если объект a является элементом множества A, то говорят, что a принадлежит A. Это записывается, как . Запись будет означать, что a не является элементом A.

Множества как объекты могут быть элементами других множеств. Множества, элементами которых являются другие множества, называются классом или семейством.

Множество, не содержащее элементов, называется пустым и обозначается .

Пункт 2. Задание множеств.

Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать разными способами:

• перечислением М элементов: ;

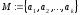• характеристическим свойством: ;

Перечисление задается в фигурных скобках, через запятую.

Здесь и далее фигурными скобками будем обозначать множество, в котором не играет роли порядок следования элементов, и круглыми скобками последовательность, в которой порядок следования элементов важен. Угловыми скобками будем обозначать совокупности элементов, имеющие неоднородную математическую природу (структуру), например, в графе имеем два вида элементов – вершины и дуги (пары) этих элементов ().

Пример 1.

.

.

Пункт 3. Операции над множествами

Множества удобно изображать с помощью кругов Эйлера (диаграмм Венна). Элементы множества изображаются точками внутри круга, если они принадлежат множеству ( на рис 1.1 а), и точками вне круга, если они множеству не принадлежат ().

b

а)

б)

Рис. 1. Иллюстрация кругами Эйлера

Будем также использовать символы вместо слов «для любых х», «каждый элемент х» и вместо слов «существует х».

Сравнение множеств

Множество A содержится во множестве B (множество B включает в себя множество A), если каждый элемент A принадлежит также и B (рис 1.1 б):

В этом случае A называется подмножеством B, а B – надмножеством A.

Если и 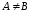, то A называется собственным подмножеством B.

Два множества равны, если они являются подмножествами друг друга, т.е..

Мощность множества обозначается как |М|. Для конечных множеств мощность – это число элементов. Например, , но .

Если А=В, то множества A и B называются равномощными.

Пример 2. Множество решений (корней) уравнения , т.е. . Множество простых чисел, меньших пяти . Следовательно, А=В.

Если в множестве A найдется хотя бы один элемент, не принадлежащий B, то A не является подмножеством B, т.е. .

Например, интервал не является подмножеством промежутка , так как , но .

Из определения следует, что любое множество является подмножеством самого себя, т.е. справедливо утверждение . Полагают, что  является подмножеством любого множества.

Пример 3. Рассмотрим множество, состоящее из трех элементов: . Найдем все его подмножества:

а) пустое ;

б) по одному

в) по два

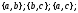
г) по три .

Число всех подмножеств составляет 8=2³. Если множество состоит из n элементов, то число всех подмножеств равно 2ⁿ. Или булеан |2^М|=2^|М|.

Пересечение множеств

Множество, состоящее из всех элементов, принадлежащих и множеству A, и множеству B, называется пересечением и обозначается .

.

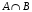Пример 4. .

Если же множества A и B не имеют общих элементов, то их пересечением является пустое множество, то есть . Например, пересечение множества четных чисел с множеством нечетных.

Пересечение пустого множества с любым множеством – пустое множество: .

Свойства пересечения

1. Коммутативность (переместительное свойство). По аналогии с а+b=b+a

.

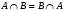2. Ассоциативность. По аналогии с

.

3. Свойство нуля. По аналогии с

.

4. Идемпотентность (аналогии нет)

.

5. Дистрибутивность. По аналогии с

;

6. Свойство единицы.

Если задан универсум U и любые , то можно записать: (рис. 1.2 а); (рис. 1.2 б).

Объединение множеств

Множество, состоящее из всех элементов, принадлежащих или множеству A, или множеству B, называется объединением множеств. Обозначается так: .

Пример 5. Даны множества и . Их объединением будет .

Пример 6. Даны числовые промежутки (рис. 1.3). Их объединением будет .

Объединение и пересечение множеств хорошо иллюстрируются на плоскости (рис. 1.4). При этом множества изображаются кругами или прямоугольниками.

Свойства объединения

Свойства объединения множеств можно сравнить со свойствами сложения чисел. Проведем аналогию этих свойств.

1. Коммутативность (переместительное свойство). По аналогии с

.

2. Ассоциативность. По аналогии с

.

3. Свойство нуля. По аналогии с

.

4. Идемпотентность (аналогии нет)

.

5. Дистрибутивность. По аналогии с

.

Рис. 3. Множества точек отрезков

Рис. 4. Операции над множествами

Разность множеств

Записывается так: .

Геометрическое представление разности множеств на рис. 1.5.

Симметричная разность (рис. 1.6):

;

.

Рис. 5. Разность множеств Рис. 6. Симметричная разность

Дополнение множеств (рис. 1.7):

;

.

Рис. 7. Дополнение множеств

Свойства дополнения :

1) ; 4) ;

2) ; 5) ;

3) ; 6) .

Пример 7. Рассмотрим операцию дополнения множества, являющегося пересечением множеств A и B. Её результат совпадает с объединением дополнений этих множеств, (свойство 6) ; в этом можно убедиться с помощью диаграмм Эйлера – Венна (рис. 1.8).

Рис. 8. Геометрическая иллюстрация свойства 6