30

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ “ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ” Кафедра “Системного аналізу та управління” Курсова робота Дисципліна “Дискретна математика" Тема „Пошук дерев на графі”(Варіант №1) Керівник роботи: доц. каф. САіУ, канд.техн.наук Волдеморт Л.М. Виконавець: студент групи ІФ-50в Поттер Г.В. Харків – 2005

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ “ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”

Кафедра “Системного аналізу та управління”

Оцінка

________________________

голова комісії

доц. каф.САиУ

____________ /Кащеєв Л.Б./

« » ___________ 200 _ р.

КУРСОВА РОБОТА

Дисципліна: „Дискретна математика”

Тема: „Пошук дерева на графі”(Варіант №1)

Виконавець: ст. гр. ИФ-50^в Г.В.Поттер

“ ” 200 р.

Керівник роботи: доц., канд. техн. наук Л.М.Волдеморт

“ ” 200 р.

Харків 2005

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ “ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ”

Кафедра “Системного аналізу та управління”

Студент Г.В.Поттер Група ИФ-50^в

ЗАВДАННЯ на науково-дослідну курсову роботу

Дисципліна: “Дискретна математика”

Тема: „Пошук дерев на графі”(Варіант №1)

Короткий зміст роботи:

а) теоретична частина

Розробка методики розв’язання задачі комівояжеру для даного графу:

, для Трента

Провести математичний опис графу; проаналізувати граф на наявність Эйлерова циклу або Эйлерова шляху; знайти остовне дерево; перевірити на присутність в графі циклів, здійснити пошук найменших шляхів з вершині 1 до усіх інших вершин, для другого (меншого графу) с завдання розрахувати кількість дерев, зайти та намалювати їх.

б) програмно-розрахункова частина

Розробка програмного забезпечення, яке реалізує пошук усіх дерев на графі та деякі інші задачі по узгодженню з керівником.

Дата видачі завдання: 15.03.2006 Термін захисту: 21.05.2006

Керівник курсової роботи: / канд. техн. наук, доц. САіУ Л.М.Волдеморт/

СОДЕРЖАНИЕ

Введение …….………..………………………………………………………..5

1 Расчетная часть работы ……………………………………………………..6

1.1 Задание на проектирование ………………………………………………6

1.2 Математическое описание графа ………………………………………...6

1.2.1 Описание графа G^ор множествами вершин V и дуг X ………...6

1.2.2 Описание графа G^ор списками смежности ……………………..6

1.2.3 Описание графа G^ор матрицей инцидентности ………………..7

1.2.4 Матрица весов соответствующего неориентированного графа .7

1.2.5 Описание графа G^ор матрицей смежности ……………………..7

1.2.6 Степени вершин неориентированного графа …………………...7

1.3 Нумерация вершин графа ………………………………………………....8

1.3.2 Нумерация вершин графа G «поиском в глубину» …………….8

1.3.2 Нумерация вершин графа G «поиском в ширину» …………….8

1.4 Эйлеров путь и Эйлеров цикл на графе ………………………………….9

1.4.1 Поиск на графе Эйлерова пути ………………………………….9

1.4.2 Построение на графе Эйлерова цикла ………………………….9

1.5 Проверка ориентированного графа на наличие циклов путем отбрасывания «истоков» и «стоков» ………………………………………….....10

1.6. Поиск остовного (остевого) дерева алгоритмом Прима-Краскала …..13

1.7. Определение дерева кратчайших путей по алгоритму Дейкстры …...15

1.8. Поиск всех деревьев на граф ……………………………………………19

2. Постановка задачи на программирование ……………………………….16

2.1. Постановка задачи ………………………………………………………16

2.2. Описание разработанного объекта ……………………………………..16

2.2.1. Иерархия наследования ………………………………………..16

2.2.2. Организация объекта ……………………..…………………….17

2.3. Интерфейс программы ………………………………………………….18

Заключение …………………………………………………………………...21

Список использованных источников ……………………………………….22

ВВЕДЕНИЕ

Теория графов – это часть науки топологии.

Граф есть упорядоченная пара (V,E), где V – непустое множество, называемое множеством вершин; E – неупорядоченное бинарное отношение на V , т.е. V&V. E называют множеством ребер. Говорят, что ребро, принадлежащее множеству E, инцидентно вершинам, которые оно соединяет. Таким образом, мы определим неориентированный граф. Он полностью определяется списком вершин и указанием, какие пары вершин имеют соединяющие их ребра (в случае нагруженного графа каждому ребру или дуге еще приписывается вес). Во многом базовые определения теории графов обязаны своему появлению Л.Эйлеру (1707-1782), решившему в 1736 г. широко известную «задачу о кенигсбергских мостах».

Ориентированный граф - упорядоченная пара (V,E), где V – множество вершин, а E – упорядоченное отношение на V (т.е. V&V). В этом случае E называют множеством дуг. Первая и вторая вершины дуги называются соответственно начальной и конечной.

В большинстве практических задач (как и в данном задании) рассматриваются графы с конечным числом ребер и вершин; их называют конечными. Для аналитического решения большинства задач желательно отойти от графического представления графов в пользу их матричного описания.

Вопросам описания графов, решению элементарных задач на графах и их программной реализации и посвящена данная работа.

1 ГРАФ

1.1 Математическое описание графа

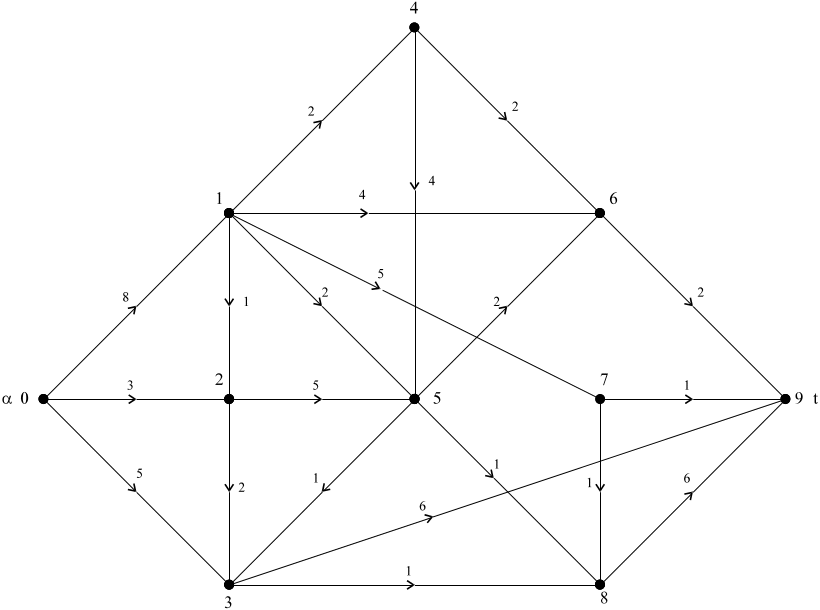
Исходный граф из задания представлен на рис1.1.

G^ор(V,X)

Рисунок 1.1 Исходный граф для расчетов

1.2.1 Описание графа G^ор множествами вершин V и дуг X:

Нумерация вершин см. рис. 1.1.

V={0,1,2,3,4,5,6,7,8,9}

X={{0,1},{0,2},{0,3},{1,2},{1,4},{1,5},{1,6},{1,7},{2,3},{2,5},{3,8},{3,9},

{4,5},{4,6},{5,3},{5,6},{5,8},{6,9},{7,8},{7,9},{8,9}}

1.2.2 Описание графа G^ор списками смежности:

Г0={1,2,3}; Г1={0,2,4,5,6,7}; Г2={0,1,3,5}; Г3={0,2,5,8,9};

Г4={1,5,6}; Г5={1,2,3,4,6,8}; Г6={1,4,5,9}; Г7={1,8,9};

Г8={1,3,5,7,9}; Г9={3,6,7,8};

1.2.3 Описание графа G^ор матрицей инцидентности:

Данный граф может описан матрицей инцидентности вершина-ребро (нумерация вершин и ребер приведена для удобства, обычно она не пишется)

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
0	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
1	1	0	0	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0
2	0	1	0	1	0	0	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0
3	0	0	1	0	0	0	0	0	1	0	1	1	0	0	1	0	0	0	0	0	0
4	0	0	0	0	1	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0	0
5	0	0	0	0	0	1	0	0	0	1	0	0	1	0	1	1	1	0	0	0	0
6	0	0	0	0	0	0	1	0	0	0	0	0	0	1	0	1	0	1	0	0	0
7	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	1	1	0
8	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	1	0	1
9	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	1	0	1	1

1.2.4 Матрица весов соответствующего неориентированного графа:

Соответствующий неориентированный граф можно представить матрицей весов:

	0	1	2	3	4	5	6	7	8	9
0	∞	8	3	5	∞	∞	∞	∞	∞	∞
1		∞	1	∞	2	2	4	5	∞	∞
2			∞	2	∞	5	∞	∞	∞	∞
3				∞	∞	1	∞	∞	1	6
4					∞	4	2	∞	∞	∞
5						∞	2	∞	1	∞
6							∞	∞	∞	2
7								∞	1	1
8									∞	6
9										∞

Примечание. Показана верхняя половина матрицы, т.к. матрица весов неориентированного графа симметрична относительно главной диагонали.

1.2.5 Описание графа G^ор матрицей смежности:

	0	1	2	3	4	5	6	7	8	9
0	∞	1	1	1	∞	∞	∞	∞	∞	∞
1	-1	∞	1	∞	1	1	1	1	∞	∞
2	-1	-1	∞	1	∞	1	∞	∞	∞	∞
3	-1	∞	-1	∞	∞	-1	∞	∞	1	1
4	∞	-1	∞	∞	∞	1	1	∞	∞	∞
5	∞	-1	-1	1	-1	∞	1	∞	1	∞
6	∞	-1	∞	∞	-1	-1	∞	∞	∞	1
7	∞	-1	∞	∞	∞	∞	∞	∞	1	1
8	∞	∞	∞	-1	∞	-1	∞	-1	∞	1
9	∞	∞	∞	-1	∞	∞	-1	-1	-1	∞

1.2.6 Степени вершин неориентированного графа:

Степени вершин рассматриваемого неориентированного графа приведены в табл.1.1

Таблица 1.1 Степенная последовательность вершин графа G

Вершины	0	1	2	3	4	5	6	7	8	9
Степени	3	6	4	5	3	6	4	3	4	4

Выбираем из таблицы наибольшую и наименьшую степени:

D_max = 6; D_min = 3.

Примечание. Степенью вершины неориентированного графа называется количество ребер, инцидентных данной вершине.

1.3.2 Нумерация вершин графа G «поисков в глубину»:

Рассмотрим стек нумерации «поиском в глубину». Правило построения LIFO – Last In First Out. Использованы номера вершин исходного графа. Просмотренные вершины выделены жирным шрифтом, уже внесенные в стек вершины заключены в скобки.

Текущая вершина	Стек дополнения	Состояние стека
0	1,2,3	01,2,3
3	8,9	0,1,2,38,9
9	пусто	0,1,2,3,8,9
8	Пусто	0,1,2,3,8,9
2	(3),5	0,1,2,3,8,95
5	(3),6,(8)	0,1,2,3,8,9,56
6	(9)	0,1,2,3,8,9,5,6
1	(2),4,(5)	0,1,2,3,8,9,5,64,7
7	(8),(9)	0,1,2,3,8,9,5,6,4,7
4	(5),(6)	0,1,2,3,8,9,5,6,4,7

Перенумерация:

Старые номера	0	3	9	8	2	5	6	1	7	4
Новые номера	0	1	2	3	4	5	6	7	8	9

Реализация нумерации представлена на рис.1.2. Исходная вершина - .

Рисунок 1.2 – Нумерация «поиском в глубину»

1.3.2 Нумерация вершин графа G «поиском в ширину»:

Рассмотрим стек нумерации «поиском в глубину». Правило построения FIFO – First In First Out. Использованы номер а вершин исходного графа. Просмотренные вершины выделены жирным шрифтом, уже внесенные в стек вершины заключены в скобки.

Текущая вершина	Стек дополнения	Состояние стека
0	1,2,3	01,2,3
1	(2),4,5,6,7	0,1,2,34,5,6,7
2	(3),(5)	0,1,2,3,4,5,6,7
3	8,9	0,1,2,3,4,5,6,78,9
4	(5),(6)	0,1,2,3,4,5,6,7,8,9
5	(3),(6),(8)	0,1,2,3,4,5,6,7,8,9
6	(9)	0,1,2,3,4,5,6,7,8,9
7	(8),(9)	0,1,2,3,4,5,6,7,8,9
8	(9)	0,1,2,3,4,5,6,7,8,9
9	Пусто	0,1,2,3,4,5,6,7,8,9

Перенумерация в данном случае не нужна, поскольку граф уже пронумерован «поиском в ширину», рис.1.3. Исходная вершина - .

Рисунок 1.3 – Нумерация «поиском в ширину»

1.3 Эйлеров путь и Эйлеров цикл на графе

1.3.1 Для определения Эйлерова путь требуется выписать степенную последовательность вершин графа G и указать в графе G Эйлеров путь. Если такового пути не существует, то в графе G добавить наименьшее число ребер таким образом, чтобы в новом графе можно было указать Эйлерову цепь.

Степенная последовательность вершин графа G:

(3,6,4,5,3,6,4,3,4,4)

Для существования Эйлерова пути допустимо только две вершины с нечетными степенями, поэтому необходимо добавить одно ребро, скажем между вершинами 4 и 7.

Полученный Эйлеров путь: 0,3,2,0,1,2,5,1,4,5,6,1,7,4,6,9,7,8,9,3,8,5,3.

Схема Эйлерова пути приведена на рис.1.4 (добавленное ребро показано пунктиром):

Рисунок 1.4 – Эйлеров путь, полученный путем добавления ребра

1.3.2 Эйлеров цикл

Эйлеров цикл позволяет обойти граф, проходя по каждому ребру только один раз. Незадействованных ребер быть не должно. Если такого цикла не существует, то в графе G добавить наименьшее число ребер таким образом, чтобы в новом графе можно было указать Эйлеров цикл.

Аналогично пункту 1.4.1 добавляем ребро {3,0}, замыкая Эйлерову цепь (при этом выполняя условие существования Эйлерова цикла - четность степеней всех вершин). Ребро {3,0} кратное, что не противоречит заданию, но при необходимости можно ввести ребра {0,7} и {4,3} вместо ранее введенных.

Полученный Эйлеров цикл: 0,3,2,0,1,2,5,1,4,5,6,1,7,4,6,9,7,8,9,3,8,5,3,0.

Схема Эйлерова цикла (добавленные ребра показаны пунктиром):

Рисунок 1.5 – добавление двух ребер для получения Эйлерова цикла

1.4 Проверка ориентированного графа на наличие циклов путем отбрасывания «истоков» и «стоков»

У нас исток вершина V₀, ее исходящие дуги X₀={(0,1),(0,2),(0,3)}, рис.1.6.

Рисунок 1.6 – Выделение первого истока

Теперь за исток принимаем вершину V₁, отбрасываем ее и дуги X₁={(1,2), (1,4), (1,5), (1,6)}, рис.1.7.

Рисунок 1.7 – Новые истоки после отбрасывания V₀

Теперь истоком стала вершина V₂, отбрасываем ее и дуги X₂={(2,3), (2,5)}, рис.1.8.

Рисунок 1.8 – Истоки после отбрасывания V₂.

В оставшемся подграфе истоком является вершина V₄, отбрасываем ее и дуги X₄={(4,6), (4,5)}.

­

Рисунок 1.9 – Истоки после отбрасывания V₄

В оставшемся подграфе истоком является вершина V₅, отбрасываем ее и дуги X₅ ={(5,3), (5,6), (5,8)}, рис.1.10.

Рисунок 1.10 – Подграф, полученный путем отбрасывания вершины V₅

В оставшемся подграфе два истока – 3 и 6, выбираем вершину V₃, отбрасываем ее и дуги X₃ ={(3,8), (3,9)}, рис.1.11.

Рисунок 1.11 – Подграф, полученный отбрасыванием вершины V₃

В оставшемся подграфе два истока – 6 и 7, выбираем вершину V₆, отбрасываем ее и ее дугу X₆ ={(6,9)}, рис.1.12.

Рисунок 1.12 – Подграф, полученный отбрасыванием вершины V₆

В оставшемся подграфе истоком является вершина V₇, отбрасываем ее и дуги X₇ ={(7,8), (7,9)}, рис.1.13.

Рисунок 1.13 – Подграф, полученный отбрасыванием вершины V₇

В результате у нас остается подграф из одной дуги. Одна дуга не может являться циклом (если это не петля в вершине), а следовательно, в результате исследования графа мы доказали, что граф G^ор циклов не имеет.

1.5 Поиск остовного (остевого) дерева алгоритмом Прима-Краскала

Выписываем таблицу весов ребер, упорядоченную по убыванию, табл.1.2.

Таблица 1.2 Веса ребер графа G

Вес	Ребра
1	(1,2), (3,8), (5,3), (5,8), (7,8), (7,9)
2	(1,5), (2,3), (4,6), (5,6), (6,9)
3	(0,2)
4	(1,6), (4,5)
5	(1,7), (2,5)
6	(3,9), (8,9)
8	(0,1)

Последовательность шагов по решению задачи Прима-Краскла:

1) выбираем ребро (1,2), окрашиваем вершины V₁ и V₂ в красный цвет;

2) выбираем ребро (3,8), обе его вершины V₃ и V₈ пока бесцветны, окрашиваем их в синий цвет;

3) следующим выбираем ребро (3,5), вершина V₃ синяя, V₅ - бесцветная, следовательно, заливаем V₅ синим цветом;

4) пытаемся выбрать ребро (5,8), но обе его вершины уже синего цвета: это ребро в решение не войдет;

5) выбираем ребро (7,8), вершина V₈ синяя, вершина V₇ пока бесцветная, закрашиваем V₇ в синий цвет;

6) выбираем ребро (7,9), вершина V₉ бесцветная, теперь будет синей;

7) выбираем ребро (1,5), его вершины разноцветные, красный цвет был задействован раньше синего, так что все синие вершины перекрашиваем теперь в красные;

8) пытаемся выбрать ребро (2,3), но обе его вершины уже красного цвета: это ребро в решение не войдет;

9) берем ребро (4,6), вершина V₆ бесцветная, теперь будет красной;

10) пытаемся выбрать ребра (5,6) и (6,9), но все их вершины уже красного цвета: эти ребра в решение не войдут;

11) берем ребро (0,2), вершина V₀ бесцветная, теперь будет красной;

12) мы выбрали 8 ребер на графе из 9 вершин, дерево построено.

Вес найденного дерева - 14. Построенное дерево приведено на рис.1.14.

Рисунок 1.14 – Остовное дерево, полученное по алгоритму Прима-Краскла