- 72 -

Лекция 6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ.

Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. В зависимости от физической природы различают: 1.Механические 2.Электромагнитные 3. Электромеханические 4. Внутриатомные и другие виды колебаний.

По характеру внешнего воздействия, оказываемого на колебательную систему различают: свободные, затухающие, вынужденные, связанные, авто и параметрические колебания. Простейшими по форме являются гармонические колебания, когда измеряемая величина изменяется по закону синуса или косинуса.

6.1. Механические гармонические колебания и их характеристики.

Дано: МТ равномерно вращается по окружности r = A с w = Const.

Найти: 1. Уравнение движения.

2. Законы изменения проекций МТ.

Движение МТ по окружности представляет собой вращение МТ вокруг центра т.О, поэтому закон движения, есть j = w t + j₀. Здесь j - угол поворота МТ за Dt, w - угловая скорость, j₀ - начальное положение МТ при t = 0. Так как МТ последовательно переходит т.1®т.2®т.3®т.4®1, то её положение в проекциях на оси, есть: x = rcos j или

x = Acos (w t + j₀ ) и y = r sin j или y = A sin(w t + j₀ ).

Анализ:

1). Движение МТ по окружности аналогично её свободным колебаниям около положения равновесия.

2). Координаты x, y - это смещения МТ из положения равновесия вдоль соответствующих осей, А - амплитуда колебаний, равная максимальному смещению, т.е. çx_max ç = A, причём всегда А > 0.

3). Величина (w t + j₀ ) - фаза колебаний, показывает долю от амплитуды, которую может иметь координата в любой момент времени. j₀ - начальная фаза - определяет положение МТ при t = 0.

Угловая скорость w называется циклической частотой, которая связана с линейной n, как w = 2pn.

4). sin и cos - периодические функции с периодом T = 2p, тогда n = и w = . Период Т - это время одного полного колебания.

5). Пусть при t = 0 j₀ = 0, тогда x = Acos w t . Выбором начала отсчёта времени всегда можно получить это условие. Так как -1 £ cosj £ 1, то смещение изменяется в пределах - A £ x £ A .

6). или . Координаты x и y сдвинуты по фазе на p/2.

7). Пусть x = Acoswt. Найдём скорость V = и ускорение смещения МТ из положения равновесия. Тогда после дифференцирования получим

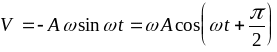, . Из сравнения следует:

а) x ,V, a - изменяются по гармоническому закону;

б) у скорости амплитуда равна Aw, у ускорения - Aw ²;

в) колебания скорости опережают колебания смещения по фазе на p/2 (или отстают на 3/2p). Для ускорения опережение составляет - p.

8). В теории колебаний наряду с тригонометрической формой записи колебаний x = Acosw t применяется и экспоненциальная форма x = A exp^iwt. Это следует из формулы Эйлера, связывающей показательную функцию мнимого аргумента exp^ix с комплексным числом cosx + isinx, где i ² = - 1 (мнимая единица). В нашем случае x = Acosw t представляется в виде x = A exp^iwt.

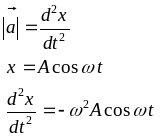
9). Для движущейся МТ по II закону Ньютона = m . После соответствующей подстановки получаем ç ç= - kx ,

- kx = , ç ç= - mw² Acosw t = - mw ² x = - kx , где k = mw² - коэффициент упругости. Тогда:

а). ç ç- является силой упругости и ç ç~ x .

б). - направлена противоположно смещению к положению равновесия.

в). При x = 0, ç ç= 0 - в положении равновесия действующая сила равна нулю.

Если сила по своей природе не является упругой, но подчиняется закону

F = - kx, то такая сила называется "квазиупругой".

10). Энергия гармонических колебаний.

В колеблющейся системе W_полн= W_к + W_р = Const (из ЗСЭ), но

Тогда

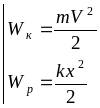
Анализ:

1. W_p и W_k - гармонические функции, W_полн - число.

2. При колебаниях W_k® W_p и W_p®W_k,, W_полн = Const.

3. При x = 0 W_k = max W_p = 0.

4. Период колебаний W_p и W_k в два раза меньше, чем период самого колебания.

5. Энергия колебаний (W_p , W_k,, W_полн) ~ A².

11). x = Acos (w t + j ) - гармоническое колебание может быть представлено в виде вектора : длина которого ç ç= A , направление образует с положительным направлением оси ОХ угол j, равный начальной фазе колебаний, вектор вращается вокруг т.О с угловой скоростью равной циклической частоте w колебаний. Графическое представление векторов лежит в основе метода векторных диаграмм.

6.2. Колебательные системы. Дифференциальное уравнение свободных колебаний.

а). Пружинный маятник (ПМ).

Тело, подвешенное на пружине представляет собой маятник .

Дано: ПМ в двух положениях: I равновесия x = 0 и II - выведенный из положения равновесия x = l.

Найти: уравнение колебаний.

В системе действует F_упр = - kx, тогда m = å _i или m = - kx После преобразования + x = 0 или + w₀ ²x = 0,

где w₀ ² = . Получили дифференциальное уравнение колебаний ПМ.

Анализ:

1). w₀² = - собственная частота колебаний ПМ.

2). Система, колебания в которой описываются уравнением +w₀ ²x = 0, называется гармоническим осциллятором.

3). Решение данного дифференциального уравнения есть выражение x = Acosw₀ t. В общем случае x = Acos (w₀ t + a) , где A и a - постоянные. Решение находится методом подбора соответствующей функции, при подстановке которой в дифференциальное уравнение получается тождество 0 º 0.

Представим x = Acosw₀ t через x = A . После соответствующих действий получим (iw₀ )² A + w₀²A = 0 или -w₀² + w₀² = 0, т.е. 0 º 0.

Итак,

x = Acosw₀ t - действительно решение данного диф-

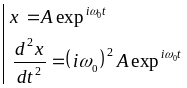
ференциального уравнения.

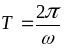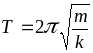4). По определению . В данном случае , тогда (период колебаний ПМ).

б). Математический маятник (ММ).

Это тело массой m, размерами которого можно пренебречь, подвешенное на нерастяжимой или невесомой нити.

Дано: ММ в двух положениях I - равновесия и II - выведен (отклонён) на малый угол a.

Найти: уравнение колебаний.

Примем знаки отклонений вдоль оси Х. Во II положении на ММ действуют силы: ç ¢ç= Pcosa , которая компенсируется силой ç ¢¢ç- натяжение нити и не оказывает влияние на параметры движения, ç ç= Psina, касательная к траектории движения, направленная к положению x = 0, т.е. относительно оси ОХ ç ç= -Psina. Здесь . В этом случае на основании II закона Ньютона m = - mgsina или + mgsina = 0. Для малых углов sina »a и sina = , тогда m + mg = 0 . Получаем + x = 0 или

+ w₀²x = 0 - дифференциальное уравнение колебаний ММ.

Анализ:

1). F = - Psina = - mg = - m x = - kx создаётся весом тела. По природе не является упругой, но подчиняется закону F = - kx, поэтому это - "квазиупругая" сила.

2). w₀ ² = - собственная частота колебаний ММ, тогда - период, который не зависит от массы ММ и амплитуды его колебаний.

3). Решение данного дифференциального уравнения есть x = Acos(w₀t + a), т.е. ММ совершает свободные гармонические колебания.

4). Параметром движения ММ можно считать и угол a, тогда из где

= - mglsina, получаем:

- mglsina или + mgla = 0.

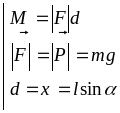
Окончательно или + w₀²a = 0.

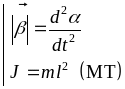
в). Физический маятник (ФМ).

Называется твёрдое тело, способное совершать колебания вокруг неподвижной оси, проходящей через произвольную точку, не совпадающую с его центром инерции. В положении равновесия эти точки находятся на одной линии.

Дано: ФМ в двух положениях (I и II).

Найти: уравнение колебаний.

При отклонении ФМ на угол a возникает вращательный момент М, обусловленный действием силы тяжести P = mg, стремящийся вернуть в положение равновесия. M = - mgd = mglsinj. Угловое ускорение = . Тогда из получим J + mglsinj = 0 или + sinj = 0. Для малых углов sinj » j и обозначая

w₀ ² = - получим дифференциальное уравнение колебаний ФМ:

+ w₀ ²j = 0.

Анализ:

1). Решение данного уравнения j = Acos (w₀t +j₀ ).

2). , отсюда период колебаний ФМ есть .

3). Величина - называется приведённой длиной ФМ, тогда 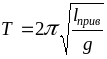. Это длина такого ММ, период колебаний которого совпадает с физическим.

4). Точка О', лежащая на расстоянии l_прив от оси вращения, называется центром качания ФМ. По теореме Штейнера J = J_c + ml , но J = m l l_пр , тогда

m l l_пр = J_c + m l ² или

l_пр = + l , т.е. l_пр > l .

5). . Для МТ J = ml ² , тогда , как для ММ.

6). Период колебаний ФМ не изменится, если поменять местами точку подвеса (т.О) и центр качаний (т.О'). Этот принцип используется в оборотном маятнике.

6.3. Затухающие колебания. Дифференциальное уравнение затухающих колебаний.

Вследствие действия в колебательной системе диссипативных сил (внутреннего трения, сопротивления воздуха и т.д.) её энергия W постепенно уменьшается. Поскольку W~A² ,то амплитуда колебаний уменьшается до нуля. Затуханием называется постепенное уменьшение амплитуды в процессе колебаний.

Дано: МТ совершает колебания вдоль оси ОХ. В системе действуют две силы _упр и _сопр .

Найти: уравнение колебаний.

Сила упругости ç ç= - kx и направлена обратно смещению. Согласно закону Стокса, сила сопротивления _c = - r , где r - коэффициент вязкого трения. Тогда m , где _упр и по II закону Ньютона можно записать в виде . Обозначим и и окончательно получаем:

.

Анализ:

1). Из обозначений - коэффициент затухания

[ b ] = [кг/с], - собственная частота колебатель- ной системы.

2). Уравнение колебаний представляет собой однородное дифференциальное уравнение 2-го порядка. Решение есть x(t) = A₀ exp^{-b t} Acos (w¢ t + j ) , т.е. гармоническое колебание с A = A₀ exp^{-b t}, частотой , начальной фазой - j.

3). График затухающих колебаний A = A₀ exp^{-b t}, cosw¢ t, j = 0.

4). Амплитуда затухающих колебаний экспоненциально уменьшается во времени, но отношение двух последовательных амплитуд остаётся Const. Величина - называется логарифмическим декрементом затуханий.

= ,

т.е. логарифмический декремент связан с T и b.

5). Частота затухающих колебаний , где - собственная частота незатухающих колебаний, b - коэффициент затухания. Математически решение имеет смысл, если > b . Кроме того, w ¢< и, соответственно, T ¢ > T, w¢- не зависит от А и поэтому не изменяется в процессе колебаний.

6). В технике используется энергетическая характеристика колебательной системы - добротность Q, которая 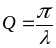или .

7). Необходимо отметить, что сила внешнего (сухого) трения F_тр не зависит от скорости, поэтому дифференциальное уравнение будет иметь другой вид.

8). Если b > , то w - мнимое число и колебательная система после однократного возмущения асимптотически возвращается в состояние покоя (асимптотическое затухание). Быстрее всего (предельный случай) это произойдёт при = b . Это предельный случай - апериодическое движение. На этом в технике основан принцип демпфирования колебаний.

9). При b = 0 получаем + ²x = 0 - уравнение свободных незатухающих колебаний.

10). l = bT ; b = ; T - время, за которое амплитуда уменьшается в e раз.

l = - число колебаний, после которого А уменьшается в e раз.

6.4. Вынужденные колебания. Дифференциальное уравнение вынужденных колебаний. Резонанс.

Если на колебательную систему с помощью связи действует периодическая сила, которая вызывает колебания системы, то возникают вынужденные колебания.

Дано: МТ совершает колебания вдоль оси ОХ. В системе действуют три силы: _упр, _c и ç ç= F_m cosw t - возмущающая сила.

Найти: уравнение колебаний.

ç _упрç = - kx, ç _cç = - r , ç _вç = F_mcosw t, тогда из получаем m = - kx - r + F_mcosw t или

+ 2b + ²x = cosw t - дифференциальное уравнение вынужденных колебаний. Неоднородное.

Анализ:

1). Обозначения: - коэффициент затухания, - собственная частота колебаний, F_m - максимальное значение возмущающей силы, w - угловая частота возмущающей силы.

2). Из теории дифференциальных уравнений: решение данного уравнения состоит из суммы: а) общего решения однородного дифференциального уравнения; б) частного решения неоднородного уравнения.

Общее решение а) найдено в разделе 6.3 и представляет собой выражение x(t) = A₀ exp^{-b t} cos(w¢ t +j), где . Пусть частное решение неоднородного дифференциального уравнения б) есть выражение x (t) = Acos(w t +a), тогда полное решение есть x (t) = A₀ exp^{-b t} cos(w¢ t +j) + A cos (w t +a).

3). Вид частного решения можно найти, используя метод векторных диаграмм. Если частное решение имеет принятый вид, то представим уравнение

, как сумму трёх слагаемых, тогда

= - Aw sin(w t +a ) = Aw cos(w t +a + ) - второе слагаемое (2) без 2b ,

= - Aw² cos(w t +a) = Aw² cos(w t +a + p) - первое (1) и

w₀²x = w₀² A cos(w t +a) - третье слагаемое (3).

Из полученных значений следует, что гармоническое колебание (4) - cosw t является суммой 3-х гармонических колебаний (1)+(2)+(3) одной и той же частоты w , поэтому при векторном представлении этих колебаний необходимо, чтобы векторная их сумма совпала с вектором возмущающей силы.

Это возможно (см. рисунок) в 2-х случаях: а) w₀ > w, б) w₀< w.

Выберем случай w₀ >w, тогда

(w₀²-w²)² A²+4b ²w ²A² = F_m² /m². Отсюда

, а

tg a = . При найденных значениях A и a полное решение дифференциального уравнения вынужденных колебаний имеет вид

x = A₀ exp^{-b t}cos(w¢ t + j) + cos(w t + arctg ).

4). В полученном решении существуют два слагаемых: первое за счёт экспоненты влияет только на начальных временных участках (режим установления колебаний I ), второе - описывает установившийся режим II. Поэтому график колебаний имеет вид:

5). Амплитуда согласно п.3 при вынужденных колебаниях зависит от частоты возмущающей силы. A ®max, если выражение в знаменателе под корнем будет®min, т.е. производная [(w₀² - w ²) ² + 4b ²w ² ] = 0. После дифференцирования получаем

2(w₀² - w²)(-2w) + 8b ²w = 0 или 4w³ - 4w₀²w + 8b ² = 0.

Преобразуем w³ - w (w₀²- 2b ²) = 0, т.е. получаем кубическое уравнение с тремя решениями: w₁ = 0 , w_2,3 = ± . Первое и третье решение не имеют физического смысла, т.к. w > 0. Поэтому полученное значение w = , при котором А = max называется резонансной частотой. Итак,

w_рез = .

Подставим w_рез в выражение и получим

A_рез= = .

6). График зависимости A = f (w) - амплитуды от частоты вынуждающей силы.

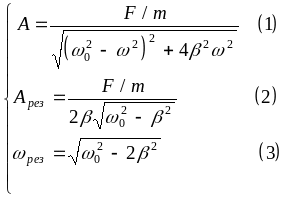
Анализ:

а). При w®0 из (1) A ® , при w®¥, A ®0.

б). Из (3) b = 0, w_рез = w₀ , A ®¥ из (1) и (2).

в). Из (2), чем меньше b , тем больше A_рез , где b₃ > b₂ > b₁ .

г). При уменьшении b максимум А сдвигается в сторону более высоких частот.

д). Из w_рез = , при 2b ² > w₀² w_рез - мнимая величина и при увеличении w амплитуда уменьшается (без максимума), начиная с b = w₀ - нижняя кривая.

е). Полученные кривые называются резонансными. Явление резкого возрастания амплитуды колебаний при совпадении частоты вынуждающей силы с собственной частотой колебательной системы, имеющей b << w₀ , называется резонансом. Согласно п.5 w = w_рез = и

при b = 0 w = w_рез = w₀ и A_рез максимальна.

6.5. Сложение колебаний.

Любая колебательная система может одновременно совершать несколько колебаний. Отдельные колебания при этом складываются в результирующее колебание. Сложение колебаний основано на принципе суперпозиции: если тело совершает несколько колебаний, то эти колебания складываются независимо друг от друга, т.е. не влияя, друг на друга. Поскольку смещение и амплитуды представляют собой вектора, то их результирующие можно вычислять известными методами: графически и алгебраически.

Следует различать: а) сложение колебаний, проходящих в одном направлении; б) сложение колебаний, происходящих во взаимно перпендикулярных направлениях.

1А. Сложение двух гармонических колебаний одинаковой частоты и распространяющихся в одном направлении.

Дано: МТ участвует в двух колебаниях , у которых A₁ ¹ A₂, а w₁ = w₂ = w = Const , распространяющихся вдоль оси ОХ.

Найти: вид и параметры результирующего колебания.

Опытным путём установлено, что в результате сложения таких колебаний, результирующее колебание является гармоническим с той же частотой w , по A_рез и w_рез , т.е. x_рез = A_рез cos(w t +j_рез ).

Необходимые параметры найдём, воспользовавшись методом векторных диаграмм, построив x₁ и x₂ . - найдём по правилу параллелограмма для векторов ₁ и ₂ , а ç ç- по теореме косинусов:

A²_рез = A₁² + A₂²-2A₁A₂ cosb, но b = 180⁰ - (j₂ - j₁), тогда

cosb = cos[180⁰ - (j₂ -j₁)] = -cos (j₂ - j₁) .

Окончательно

A²_рез = A₁² + A₂²-2A₁A₂ cos(j₂ - j₁).

j_рез (из рис.) можно найти: tgj_рез = ,

j_рез = arctg .

Результирующее колебание будет иметь вид:

x_рез = A_рез cos(w t + arctg ).

Частные случаи. 1) Пусть j₂ - j₁ = 0, т.е. cos(j₂ -j₁) = 1, что соответствует j₂ -j₁ = 2pn, где n = 0,±1, ±2 ..., т.е. совпадению исходных колебаний по фазе. В этом случае A²_pез = A₁² + A₂² + 2A₁A₂ = (A₁ + A₂)² или A_рез = A₁ + A₂ , т.е. результирующая амплитуда равна сумме амплитуд.

2) Пусть j₂ -j₁ = (2n + 1)p , где n = 0,±1, ±2 ..., тогда cos(j₂ -j₁) = -1, т.е. исходные колебания находятся в противофазе. Результирующее колебание в этом случае находится в фазе с одним из исходных колебаний, а A_рез= (A₁ - A₂)² или A_рез= ç A₁ - A₂ç. Если A₁ = A₂ , то колебания взаимно уничтожаются.

2а. Колебания, происходящие в одном направлении с разными частотами.

Результирующее колебание в этом случае является негармоническим, но A_рез= A₁ ± A₂ , т.е. находится алгебраически. С другой стороны, любое негармоническое колебание можно представить как результирующее нескольких гармонических колебаний с циклическими частотами, кратными основной w = . Такое представление называется анализом Фурье.

Особый случай, если частоты двух колебаний близки, т.е.

, где A₁= A₂ = A,

а Dw << w₁ и Dw << w₂. Пусть w₁=w₂ =w. Сложим эти колебания

x_рез = x₁ + x₂ = (2A cos t)cos (w t + t)

Так как <<w, этим слагаемым пренебрегаем, тогда

x_рез = (2A cos t) cosw t.

Анализ:

1). Если рассматривать x_рез как гармоническое колебание, то 2A cos t - это его амплитуда, которая пульсирует с частотами .

2). График колебаний определяется соотношением . На рисунке = G.

3). Амплитуда колебаний изменяется гораздо медленнее T_A > T.

4). Такие колебания называются биениями.

б. Сложение взаимно перпендикулярных колебаний.

Если тело (МТ) участвует одновременно в двух колебаниях , то результирующее смещение в любой момент времени определяется как векторная сумма, причём ç ç= , а j = arctg . В данном случае и j - представляют собой полярные координаты результирующего смещения. Параметрами в полярных координатах являются: радиус-вектор , определённой величины и угол j , между и осью ОХ. Если соединить последовательно результирующие смещения, то в плоскости ХY получится траектория результирующего колебания, которая представляет собой сложную кривую, называемую фигурами Лиссажу. Форма данных фигур зависит и определяется соотношением частот w₁ и w₂ и разностью начальных фаз, т.е Dj = j₂ - j₁ .

Рассмотрим эти частные случаи.

Пусть МТ участвует одновременно в двух колебаниях вдоль осей OX и OY, т.е. , где w₁ = w₂ = w , j₁ = 0, j₂ = Const . Для нахождения траектории движения МТ исключим из данных уравнений время.

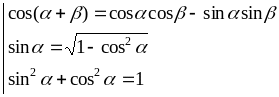
После подстановки = cosj - ( )sinj и преобразования получим

- cosj = - sinj. Обе части равенства возведём в квадрат

( - cosj)² = . Раскроем скобки и преобразуем

- 2 cosj + (sin ²j+ cos ²j) = sin ²j или

+ - 2 cosj = sin²j .

Полученное уравнение траектории - это уравнение эллипса с произвольно ориентированными осями.

Частные случаи: а) Пусть j =0, тогда sinj =0, cosj =1 и уравнение преобразуется ( - )² = 0 или = .

Отсюда y = - уравнение прямой.

Выберем (произвольно) т.1, с координатами (Х,Y) ç ç= , но x = Acosw t , а y = B cosw t . Отсюда r = cosw t - получили уравнение колебаний с амплитудой вдоль прямой.

б) Пусть j = p , тогда

sinj = 0, cosj = -1. ( + )² = 0 или

- = , y = - получаем случай а) для прямой.

в) Пусть j = , тогда cosj = 0, sin²j = 1 и уравнение + = 1 - траектория движения МТ представляет собой эллипс с осями, совпадающими с координатами.

г) Пусть j = , а A = B , тогда cosj = 0, sinj = 1 и x² + y² = 1 - траекторией движения является окружность.