
- •220400 Алгебра и геометрия Толстиков а.В.
- •Изучаемые вопросы
- •Задачи для решения в аудитории и на дом
- •Задача для контроля изученного материала
- •Задача для контроля изученного материала
- •220400 Алгебра и геометрия Толстиков а.В.
- •Изучаемые вопросы
- •Задачи для самостоятельного решения в аудитории и на дом
- •Задачи для контроля изученного материала
Задача для контроля изученного материала
|
Формулировка задачи |
1 вариант |
2 вариант |
1 |
Пусть x = (x1, x2, x3). Найти собственные векторы и собственные значения линейного оператора A. |
Ax = (5x1-x2, 6x1+2x2, -3x1+x2- x3) |
Ax = (3x1-4x2+4x3, x1-x2 -x3, -2x3) |
Ответы:
1.
=0 , b
= t
(1,
0, 0), tR/{0}
.
2.
1)
=1 , b
= t
(1,
0, 0), tR/{0};
2) 1
=-1 , b
= t
(0,
-1, 1), tR/{0};
2=
=![]() ;
;3=
;
;3=![]() .
3)
1
=1 , b
= t
(1,
1, 1), tR/{0};
1
=0 , b
= t
(0,
0, 1), tR/{0};
4)
1
=0 , b
= t
(1,
-1, 1), tR/{0};
2
=1 , b
= t
(-1,
0, 1), tR/{0};
3
=3 , b
= t
(1,
2, 1), tR/{0}.
.
3.
1)
=1 , b
= t
(1,
0), tR/{0};
1
=3 , b
= t
(1,
2), tR/{0};
2)
нет.
4.
1) не имеет. 2)
=1 , b
= t
(1,
0), tR/{0};
1
=0 , b
= t
(0,
1), tR/{0};
3)
1
= k
, b
= t1
(1,
0)+ t2
(0,
1), t1,
t2R/{0}.
5.
1) 1
=
.
3)
1
=1 , b
= t
(1,
1, 1), tR/{0};
1
=0 , b
= t
(0,
0, 1), tR/{0};
4)
1
=0 , b
= t
(1,
-1, 1), tR/{0};
2
=1 , b
= t
(-1,
0, 1), tR/{0};
3
=3 , b
= t
(1,
2, 1), tR/{0}.
.
3.
1)
=1 , b
= t
(1,
0), tR/{0};
1
=3 , b
= t
(1,
2), tR/{0};
2)
нет.
4.
1) не имеет. 2)
=1 , b
= t
(1,
0), tR/{0};
1
=0 , b
= t
(0,
1), tR/{0};
3)
1
= k
, b
= t1
(1,
0)+ t2
(0,
1), t1,
t2R/{0}.
5.
1) 1
=![]() ,
1
=
,
1
=![]() ;
2)
=0 , b
= t
(1,
-2), tR/{0};
1
=7 , b
= t
(1,
1/3) , tR/{0};
2)
=2 , b
= t
(1,
-3/2), tR/{0};
1
=7 , b
= t
(1,
1) , tR/{0};
4)
1
=1 , b
= t
(1,
0, 1), tR/{0};
2
=2 , b
= t
(1,
0, 0), tR/{0};
3
=-1 , b
= t
(0,
1, 1), tR/{0};
5)
1
=-1 , b
= t
(1,
0, 0), tR/{0};
2
=2, b
= t
(1,-3,-3),
tR/{0};
6)
1
=-1 , b
= t
(-1,
-1, 1), tR/{0};
7)
1
=0 , b
= t
(3/2,
-1/2, 1), tR/{0}.
Дома: Линейные операторы в
евклидовых пространствах.
;
2)
=0 , b
= t
(1,
-2), tR/{0};
1
=7 , b
= t
(1,
1/3) , tR/{0};
2)
=2 , b
= t
(1,
-3/2), tR/{0};
1
=7 , b
= t
(1,
1) , tR/{0};
4)
1
=1 , b
= t
(1,
0, 1), tR/{0};
2
=2 , b
= t
(1,
0, 0), tR/{0};
3
=-1 , b
= t
(0,
1, 1), tR/{0};
5)
1
=-1 , b
= t
(1,
0, 0), tR/{0};
2
=2, b
= t
(1,-3,-3),
tR/{0};
6)
1
=-1 , b
= t
(-1,
-1, 1), tR/{0};
7)
1
=0 , b
= t
(3/2,
-1/2, 1), tR/{0}.
Дома: Линейные операторы в
евклидовых пространствах.
220400 Алгебра и геометрия Толстиков а.В.
Курс 1. Семестр 1. Практическое занятие 15. Линейные операторы в евклидовых пространствах
Изучаемые вопросы
Определение сопряженного оператора. Матрица сопряженного оператора в ортонормированном базисе. Самосопряженный оператор. евклидовых пространствах и их свойства. Матрица самосопряженного оператора в ортонормированном базисе. Построение ортонормированного базиса из собственных векторов самосопряженного оператора. Ортогональные матрицы и их свойства. Ортогональные операторы и их свойства.
Задачи для самостоятельного решения в аудитории и на дом
Найдите сопряженный оператор A* для оператора A поворота пространства V2 векторов плоскости на угол . Вычислить матрицу оператора A*.
Найдите сопряженный оператор A* для нуль-оператора A. Вычислить матрицу оператора A*.
Найдите сопряженный оператор A* для тождественного оператора A. Вычислить матрицу оператора A*.
Найдите сопряженный оператор A* для оператора A подобия пространства V2. Вычислить матрицу оператора A*.
Являются ли операторы из упражнений 1-4 самосопряженными.
В линейной оболочке L = L(sin x, cos x) скалярное произведение элементов f1 = A1sin x + B1cos x, f2= A1sin x + B1cos x введено по формуле. (f1, f2) = A1A2 + B1B2. Найти оператор, сопряженный к оператору дифференцирования, действующему в пространстве L. Доказать, что оператор дифференцирования действующий в пространстве L является ортогональным.
В линейной оболочке L = L(sin x, cos x) скалярное произведение элементов f1 = A1sin x + B1cos x, f2= A1sin x + B1cos x введено по формуле. (f1, f2) = A1A2 + B1B2 + (1/2)(A1B2 + B1A2). Найти ортонормированный базис пространства . Найти матрицу оператора и сопряженного. Является ли оператор самосопряженным.
Найти собственные векторы и собственные значения линейного оператора, действующего в евклидовом пространстве и имеющего в ортонормированном базисе e1, e2, e3 матрицу. Составить матрицу из собственных значений.
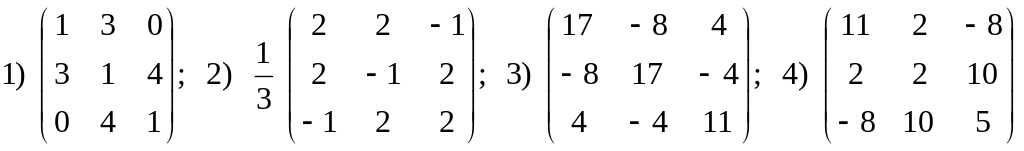 .
.
Найти матрицу сопряженного оператора A* в базисе f1= e1+ e2+ e3, f2=e2+ e3, f3=e2- e3, e1, e2, e3 - ортонормированный базис, если матрица линейного оператора A евклидова пространства в базисе f1, f2, f3 равна
 .
.Линейный оператор A, действующий в евклидовом пространстве, имеет в базисе f1= e2+ e3, f2=e1+ e3, f3=e1+e3, e1, e2, e3 - ортонормированный базис, матрицу
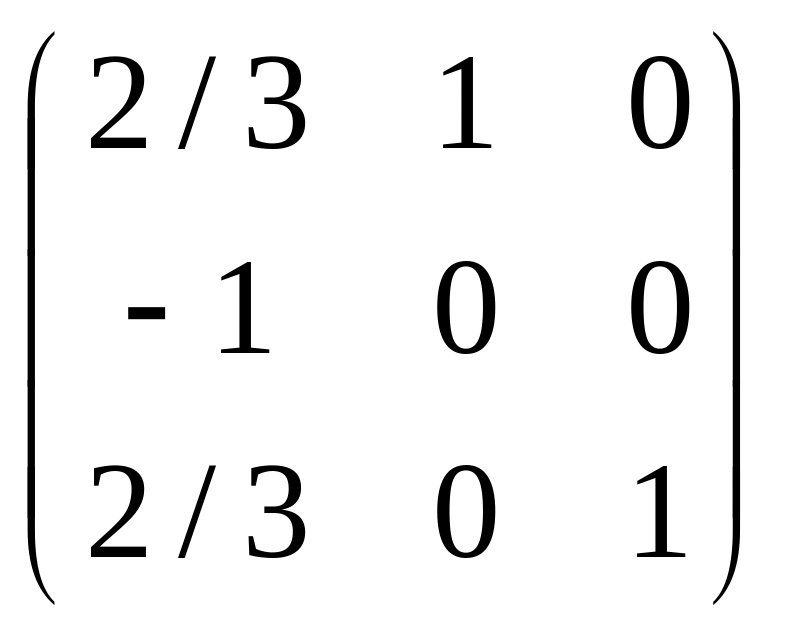 .
Является ли оператор ортогональным?
.
Является ли оператор ортогональным?
