Лабораторная работа № 12

Исследование процессов затухания в колебательном контуре

Цель работы: исследовать затухающие колебания в контуре,

содержащем индуктивность, емкость и сопротивление,

возбуждаемые периодически повторяющимися

короткими импульсами тока.

Приборы: генератор импульсов, магазин сопротивлений «МСР-60М», магазин емкостей «Р-513», осциллограф «ЕО-213».

ВСТАВИТЬ ФОТОГРАФИЮ

Краткая теория

В данной работе исследуются затухающие колебания в контуре, содержащем индуктивность, емкость и сопротивление, возбуждаемые периодически повторяющимися короткими импульсами тока. Для получения импульсов, возбуждающих колебания в контуре, используется мультивибратор. Наблюдается временная развертка этих колебаний на экране осциллографа.

ЗАТУХАЮЩИЕ КОЛЕБАНИЯ

1. Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой. Свободные колебания реальных систем всегда затухают. Затухание в электрических колебательных системах называется тепловыми потерями в проводниках, образующих систему или находящихся в ее переменном электрическом поле, потерями энергии на излучение электромагнитных волн, а также тепловыми потерями в диэлектриках.

Закон затухания колебаний зависит от свойств колебательной системы. Система называется линейной, если параметры, характеризующие существенные в рассматриваемом процессе физические свойства системы, не изменяются в ходе процесса. Линейные системы описываются линейными дифференциальными уравнениями. Например, электрический колебательный контур можно считать линейной системой, если его электрическое сопротивление , электроемкость и индуктивность не зависят ни от тока в контуре, ни от напряжения. В большинстве случаев реальные колебательные системы достаточно близки по своим свойствам к линейным.

2. Дифференциальное уравнение свободных затухающих колебаний линейной системы имеет вид:

(1)

Здесь — изменяющаяся при колебаниях физическая характеристика системы, — коэффициент затухания, а — циклическая частота свободных незатухающих колебаний той же системы, т. е. в отсутствие потерь анергии (при ).

Пример 1. Свободные затухающие колебания в электрическом колебательном контуре. Электрическое сопротивление реального контура и дифференциальное уравнение колебаний в контуре имеет вид:

(2)

где и .

3. Если затухание не слишком велико ( < ) зависимость от , удовлетворяющая уравнению затухающих колебаний (п. 2) имеет вид:

(3)

Здесь , а постоянные величины и ‚ зависят от начальных условий, т. е. от значений в в начальный момент времени ( ). График зависимости от при показан на рис. 1.

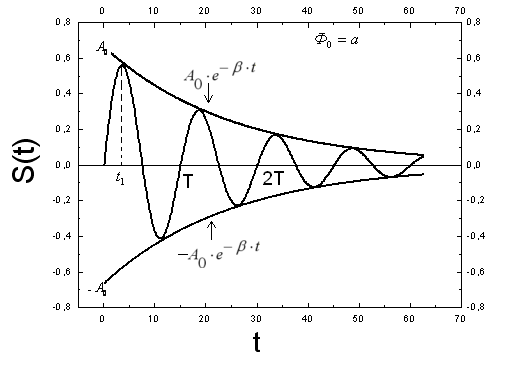
Рис. 1.

Затухающие колебания не являются периодическими. Например, максимальное значение колеблющейся величины , достигаемое в некоторый момент времени , в последующем при никогда не повторяется. Однако при затухающих колебаниях величина обращается в нуль, изменяясь в одну и ту же сторону (например, убывая), а также достигает максимальных и минимальных значений через равные промежутки времени:

. (4)

Поэтому величины и условно называют периодом (условным периодом) и циклической частотой (условной циклической частотой) затухающих колебаний. Величина

(5)

называется амплитудой затухающих колебаний, соответственно — начальной амплитудой. Амплитуда затухающих колебаний уменьшается с течением времени и тем быстрее, чем больше коэффициент затухания .

Промежуток времени , в течение которого амплитуда затухающих колебаний уменьшается в раз, называется временем релаксации.

4. Логарифмическим декрементом затухания называется безразмерная величина , равная натуральному логарифму отношения значений амплитуды затухающих колебаний в моменты времени и ( — условный период колебаний),

(6)

где — число колебаний, в течение которых амплитуда уменьшается в раз. Связь между циклической частотой затухающих колебаний системы и логарифмическим декрементом затухания определяется как:

. (7)

Колебательный контур

Рассмотрим контур, состоящий из индуктивности, емкости и сопротивления. Изучим процессы, происходящие в этой системе. Схема на рис. 2 представляет собой контур из последовательно соединенных .

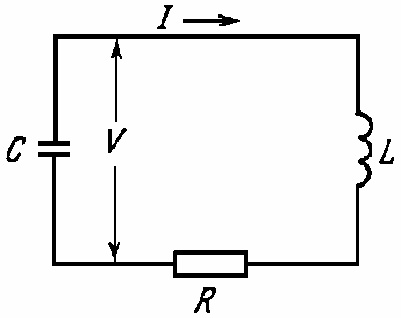
Рис. 2. Контур с последовательным соединением .

Обозначим через заряд, находящийся в момент времени на емкости . Разность потенциалов, или напряжение, на емкости обозначим через ; очевидно, что это же напряжение приложено и к последовательно соединенным индуктивности и сопротивлению .

Примем за положительное напряжение такое напряжение, когда верхняя Пластина конденсатора заряжена положительно, и укажем стрелкой на рис. 1 положительное направление тока. При выбранных таким образом знаках соотношения, связывающие заряд , ток и напряжение на емкости , имеют следующий вид:

(1)

Мы хотим исключить две из трех переменных . Из двух первых уравнений мы получаем, после чего третье уравнение принимает вид

или (2)

Это — дифференциальное уравнение второго порядка с постоянными коэффициентами. Попробуем взять в качестве решения следующую функцию:

, (3)

где , и - постоянные величины. Первая и вторая производные от этой функции равны

(4)

(5)

Подставляя эти величины в уравнение (2) и сокращая на множитель , получим

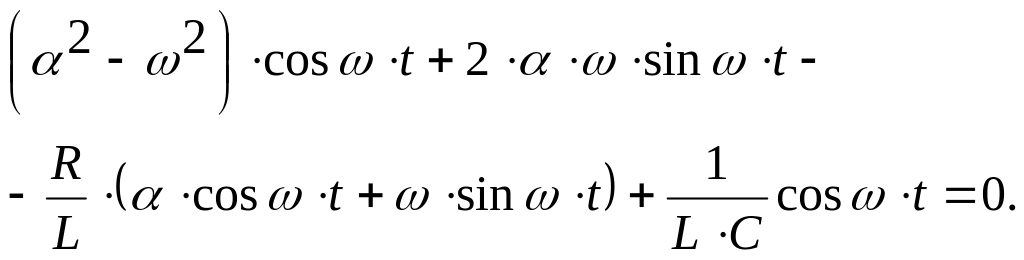(6)

Это выражение будет справедливо для всех тогда и только тогда, когда коэффициенты при и равны нулю. Иными словами, должны, выполняться условия

(7)

и

(8)

Первое из этих уравнение дает следующее значение

(9)

Из второго уравнения следует

(10)

Так как постоянная представляет собой действительное число, то не может иметь отрицательного значения. Следовательно, уравнение (3) будет решением уравнения (2) только при ( ). Действительно, мы хотим исследовать случай «слабого затухания», что соответствует малому сопротивлению. Поэтому предположим, что значения контура обеспечивают выполнение неравенства .

Функция не является единственным возможным решением. С таким же успехом можно, принимая значения и из уравнений (9) и (10), взять в качестве решения функцию . Общее решение будет равно сумме частных решений:

(11)

Произвольные постоянные и должны быть выбраны такими, чтобы удовлетворить начальным условиям. Эта проблема не представляет для нас большого интереса. В каждом данном случае решение может содержать синус или косинус или их суперпозицию, и это не более принципиально, чем вопрос о начале хода часов. Существенным является наличие затухающих синусоидальных колебаний.

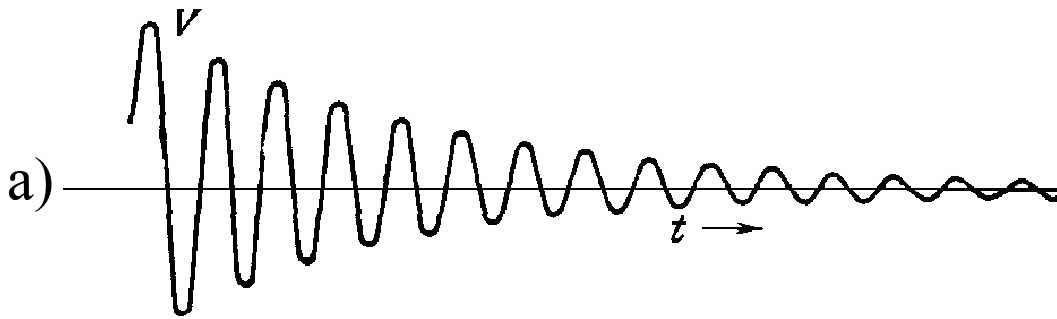
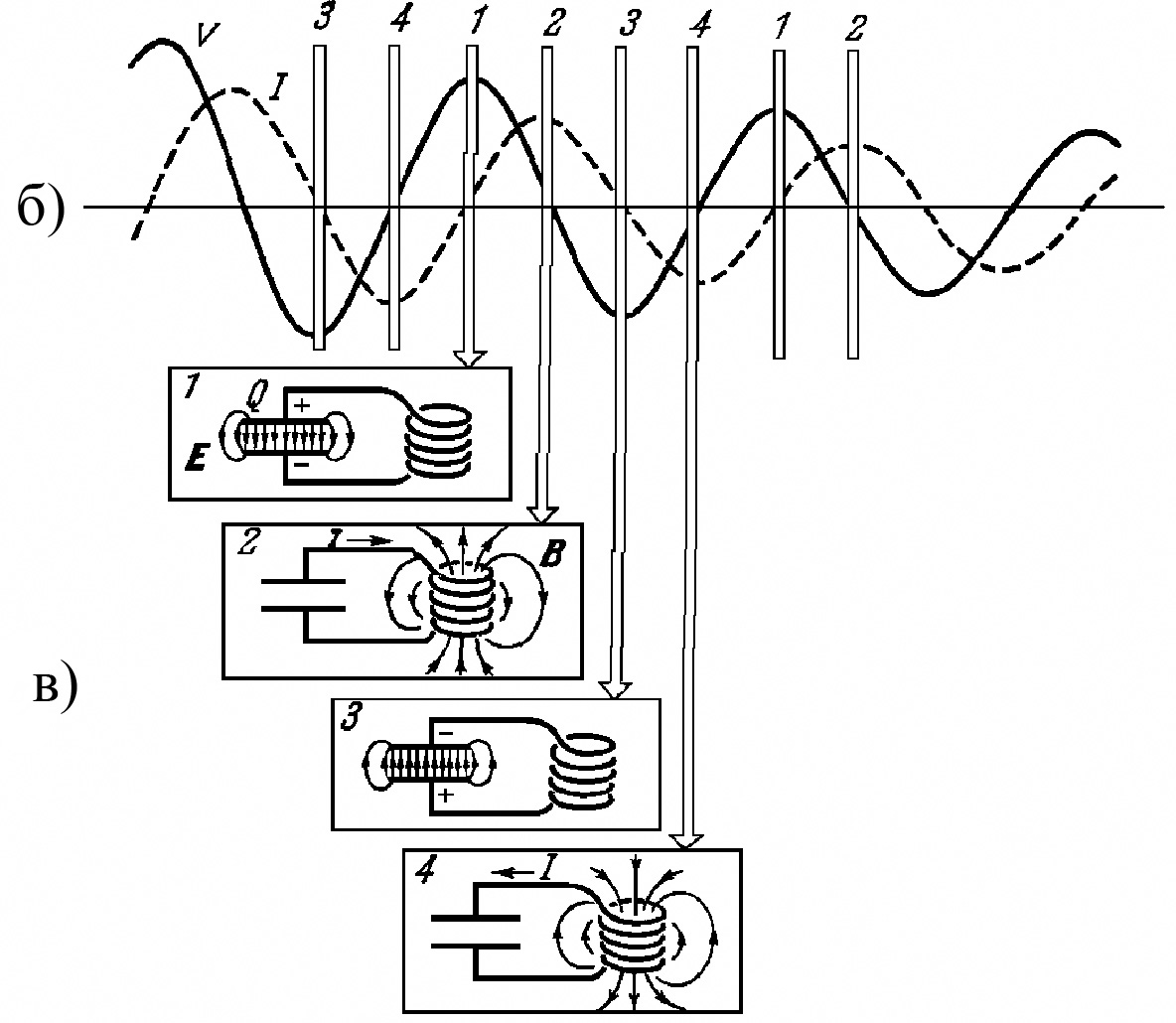
Рис. 3. а) Затухающее синусоидальное колебание напряжения в -

контуре; б) Часть кривой графика (а) с растянутой шкалой

времени и кривой тока ; в) Периодический переход энергии

от электрического поля к магнитному и обратно.

Зависимость напряжения от времени показана на рис. 3, а. На рис. 3, б шкала времени растянута и штрихом показан ток . Пусть напряжение описывается затухающей косинусоидой (уравнение (3)). Тогда ток следующим образом зависит от времени:

. (12)

Отношение является мерой затухания. Если это отношение очень мало, то за время, в течение которого амплитуда уменьшается незначительно, происходит большое число колебаний.

Для рис. 3 мы принимаем . Тогда член с косинусом уравнении (12) будет невелик. Наличие этого члена приведет к сдвигу фазы колебаний на небольшой угол, равный . Поэтому колебания тока отстают по фазе от колебания напряжения почти точно на четверть периода.

Эти колебания сводятся к переходу энергии от конденсатора к индуктивности, т. е. от электрического поля к магнитному, и обратно. В момент времени, обозначенный на рис. 3, б цифрой 1, вся энергия сосредоточена в электрическом поле. Через четверть периода, в момент времени 2, конденсатор разряжен и почти вся энергия перешла в магнитное поле катушки. Во время этих колебаний, из-за наличия сопротивления R. энергия, запасенная в полях, постепенно уменьшается.

Относительное затухание осциллятора часто выражается величиной обозначаемой , которая называется «коэффициентом добротности». Чем меньше затухание, тем больше . Для осциллятора с частотой величина представляет собой безразмерное отношение следующего вида:

. (13)

Важно запомнить, что есть число радиан в угле (т. е. , умноженное на число колебаний), соответствующее уменьшению энергии колебаний в раз.

Энергия, запасенная в нашем контуре, пропорциональна , или , и, следовательно, пропорциональна . Она уменьшается в е раз за время , что соответствует радиан. Итак, для нашего - контура

. (14)

Дайте приблизительную оценку для колебания, изображенного на рис. 3.

Очевидно, что рассмотренный нами случай включает в себя ряд более простых. Если , мы имеем осциллятор без всякого затухания с частотой , равной

(15)

В системах, с которыми мы имеем дело, затухание часто бывает достаточно мало и при вычислении частоты им можно пренебречь. Затухание влияет на частоту только во втором порядке.

Для полноты описания кратко рассмотрим явления, когда В этом случае общее решение уравнения (2) имеет вид

(16)

Таким образом, колебаний нет, есть только монотонное затухание. В специальном случае «критического» затухания , , и решение дифференциального уравнения (2) принимает вид

(17)

При этих условиях полная энергия в контуре с заданным и рассеивается наиболее быстро. На рис. 4 показаны все способы поведения

колебательного контура: здесь приведены кривые разности потенциалов для двух контуров со слабым затуханием, для контура с критическим и для контура с сильным затуханием.

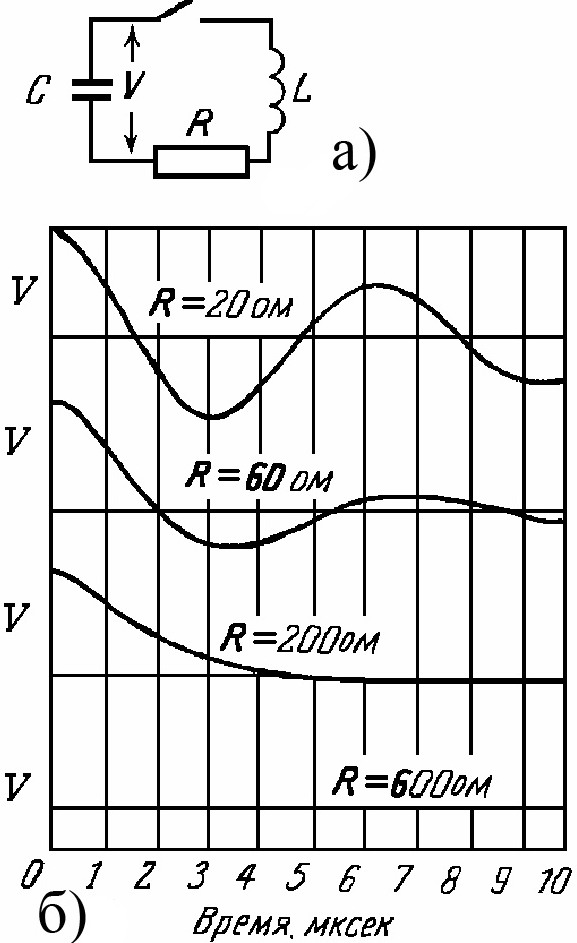
Рис. 4. а) Конденсатор заряжен, ключ замыкается в момент

( ). б) Показаны четыре

случая, один из которых при , является

случаем критического затухания.

Емкость и индуктивность в этих четырех случаях одни и те же; изменяется только сопротивление. Собственная угловая частота для этого контура равна . В периодах в секунду это составляет , или .

Чтобы возбудить контур, нужно зарядить конденсатор до некоторой разности потенциалов, скажем в , и затем в момент времени замкнуть ключ. Таким образом при представляет собой первое начальное условие. условие. При равен нулю и ток , так как индуктивность не позволит току возрасти мгновенно. Следовательно, второе начальное условие, налагаемое на , заключается в том, что при . Заметьте, что все четыре кривые вначале спадают одинаково. В случае сильного затухания ( ) большая часть кривой близка к простой убывающей экспоненте для -контура. Присутствие индуктивности сказывается только в самом начале, где кривая идет параллельно оси абсцисс.

Описание установки

Принципиальная электрическая схема установки изображена на рис. 5. Эскизная схема установки представлена на рис. 6. Она состоит из автоколебательного мультивибратора, эмиттерного повторителя, емкости, индуктивности, сопротивления, осциллографа и монтажных проводников.

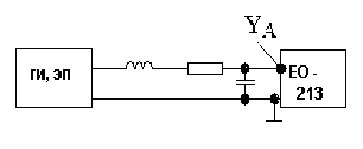
Рис.5.Электрическая схема.

Рис. 6. Схема соединений установки.

Фронты и спады прямоугольных импульсов возбуждают затухающие колебания в колебательном контуре, которые можно наблюдать на осциллографе. Колебательный контур собирается из магазина емкостей и набора индуктивностей (катушек).