Лекция 13

ЛИНЕЙНОЕ ПРОСТРАНСТВО

13.1 Определение линейного пространства

Определение. Множество R, состоящее из элементов , для которых определена операция сравнения, называется линейным пространством, если

(1). Каждой паре элементов этого множества поставлен в соответствие третий элемент этого же множества, называемый их суммой и обозначаемый , таким образом, что выполнены аксиомы

а) ;

б) ;

в) существует нулевой элемент , такой, что для любого имеет место ;

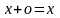г) для каждого существует противоположный элемент , такой, что .

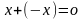(2). Для любого элемента и любого числа существует такой принадлежащий R элемент, обозначаемый и называемый произведением числа на элемент, что выполнены аксиомы:

а) ;

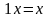б) .

(3). Для операций сложения элементов и умножения элемента на число выполнены аксиомы дистрибутивности:

а) ;

б) 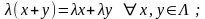и для любых чисел .

Замечание. Первая группа аксиом равносильна требованию, чтобы R являлось абелевой группой относительно операции сложения.

Линейным пространством является :

(1). Множество всех векторов на плоскости.

(2). Множество всех векторов в пространстве.

(3). Множество всех n-компонентных столбцов.

(4). Множество всех многочленов степени не выше, чем n.

(5). Множество всех матриц размера .

(6). C[a,b] – множество всех функций, непрерывных на [a,b].

(7). Множество всех решений однородной системы m линейных уравнений с n неизвестными

Теорема 13.1 Линейное пространство имеет единственный нулевой элемент.

Доказательство.

Пусть существуют два различных нулевых элемента и . Тогда, согласно аксиоме (1) пункт (в) из определения линейного пространства, будут справедливы равенства

и .

Откуда в силу коммутативности операции сложения получаем .

Теорема доказана.

Теорема 13.2 Для каждого элемента x линейного пространства имеет место равенство .

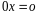Доказательство.

Из аксиоматики линейного пространства имеем

Прибавляя к обеим частям равенства элемент y, противоположный элементу x, получаем, что .

Теорема доказана.

Теорема 13.3 Для каждого элемента линейного пространства существует единственный противоположный элемент.

Доказательство.

Пусть для элемента x существуют два различных противоположных элемента и . Тогда, согласно аксиоме (1) пункт (г) линейного пространства, будут справедливы равенства и . Прибавим к обеим частям первого равенства элемент , получим

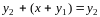
в силу ассоциативности операции сложения и второго равенства. Но, с другой стороны,

.

То есть .

Теорема доказана.

Теорема 13.4 Для каждого противоположным элементом служит элемент .

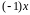Доказательство.

Из аксиоматики линейного пространства и в силу теорем 13.2–13.3 имеем

.

Это равенство и означает, что противоположный к x элемент имеет вид .

Теорема доказана.

13.2 Линейная зависимость, размерность и базис в линейном пространстве

Определение.

1. Выражение 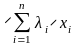называется линейной комбинацией элементов линейного пространства R.

2. Элементы линейного пространства R называются линейно зависимыми, если существуют числа , не равные нулю одновременно, такие, что .

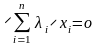3. Элементы линейного пространства R называются линейно независимыми, если из равенства следует, что .

Лемма 13.1 Для того чтобы некоторое множество элементов линейного пространства было линейно зависимым, необходимо и достаточно, чтобы один из этих элементов являлся линейной комбинацией остальных.

Доказательство.

Доказательство дословно совпадает с доказательством леммы 1 из первой лекции, в котором слово “вектор” следует заменить словом “элемент”.

Лемма 13.2 Если некоторое подмножество элементов линейно зависимо, то линейно зависимы и сами элементы .

Доказательство.

Без ограничения общности можно предположить, что линейно зависимое подмножество состоит их первых элементов множества . Тогда существуют не равные нулю одновременно числа , такие, что . Но из этого соотношения вытекает равенство , которое означает линейную зависимость элементов .

Лемма доказана.

Определение. Базисом в линейном пространстве R называется любой упорядоченный набор его n элементов, если

(1). эти элементы линейно независимые;

(2). любое подмножество в R, содержащее элемент, включая эти n элементов, линейно зависимо.

Определение. Линейное пространство R называется n-мерным и обозначается , если в нем существует базис, состоящий из n элементов. Число n называется размерностью линейного пространства и обозначается .

Теорема 13.4 Для каждого элемента линейного пространства существует единственное представление в виде линейной комбинации базисных элементов.

Доказательство.

Пусть в линейном пространстве заданы базис и произвольный элемент x. Тогда, по определению базиса, система элементов линейно зависима и по лемме 13.1 элемент x является линейной комбинацией элементов . Существование разложения таким образом доказано.

Покажем теперь единственность разложения. Допустим, что существуют две различные линейные комбинации и . Тогда получаем, что

,

но это означает, что при данном допущении система элементов линейно зависима. Полученное противоречие доказывает единственность.

Теорема доказана.

В общем случае линейное пространство может не иметь базиса. Таким свойством обладает, например, линейное пространство, состоящее из одного нулевого элемента.

В таблице приведены примеры базисов в линейных пространствах.