
ПРЕОБРАЗОВАНИЯ ПЛОСКОСТИ
Лекция 11
11.1 Произведение матриц
Определение. Матрица
 размера
размера
 ,
с элементами
,
с элементами
 ,
называется произведением
матрицы
,
называется произведением
матрицы
 размера
размера
 ,
с элементами
,
с элементами
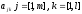 )
на матрицу
)
на матрицу
 размера
размера
 ,
с элементами
,
с элементами

 ),
где
),
где

Замечания о произведении матриц
Из определения произведения матриц непосредственно следует, что для матриц подходящих размеров:
-
произведение матриц некоммутативно, то есть в общем случае
 ,
,
-
произведение матриц ассоциативно
 ,
,
-
произведение матриц обладает свойством дистрибутивности
 .
.
Отметим еще раз, что произведение двух матриц существует только тогда, когда число столбцов первого сомножителя равно числу строк второго.
Легко
убедиться, что умножение (как справа,
так и слева) любой матрицы
 на подходящего размера единичную матрицу
на подходящего размера единичную матрицу
 дает в результате ту же самую матрицу
дает в результате ту же самую матрицу
 .
.
Определение.
Матрица
 называется обратной
квадратной матрице
называется обратной
квадратной матрице
 ,
если выполнены равенства
,
если выполнены равенства
 .
.
Обратная
матрица существует не для всякой
произвольной квадратной матрицы. Для
существования матрицы, обратной к
 ,
необходимо и достаточно, чтобы выполнялось
условие
,
необходимо и достаточно, чтобы выполнялось
условие
 .
.
Определение.
Матрица
 ,
для которой
,
для которой
 ,
называется вырожденной,
а матрица, для которой
,
называется вырожденной,
а матрица, для которой
 ,
– невырожденной.
,
– невырожденной.
Лемма 10.1 Если обратная матрица существует, то она единственна.
Доказательство.
Предположим,
что невырожденная матрица
 имеет две обратные:
имеет две обратные:
 и
и
 .
Тогда из равенств
.
Тогда из равенств
 и
и
 следует, что
следует, что
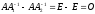 .
.
Умножая
слева обе части данного равенства на
 ,
получаем
,
получаем

и,
учтя, что
 ,
приходим к равенству
,
приходим к равенству
 .
.
Лемма доказана.
Для
квадратных матриц порядка
 справедливы следующие равенства:
справедливы следующие равенства:

 если
если
 .
.
Пример 1. Используя матричные операции, систему линейных уравнений

можно записать в виде
 ,
,
где

 ,
,
а
ее решение (если существует
 )
– в виде
)
– в виде
 .
.
Пример 2. Формулы перехода от одной декартовой системы координат к другой с помощью матричных операций могут быть записаны в виде

 ,
,
где S – матрица перехода.
Теорема 11.1 Имеет место соотношение
 .
.
Теорема 11.2 Для невырожденных одинакового размера квадратных матриц A и B справедливо соотношение
 .
.
Задача
на дом: Проверить тождество

Определение.
Невырожденная квадратная матрица Q,
для которой
 ,
называется ортогональной.
,
называется ортогональной.
Свойства ортогональных матриц играют важную роль во многих приложениях. Их можно сформулировать в виде следующих теорем.
Теорема
11.3 Для
ортогональной матрицы Q
справедливо равенство
 .
.
Доказательство.
Умножая
равенство
 последовательно слева на
последовательно слева на
 ,
в силу определения обратной матрицы
приходим к соотношению
,
в силу определения обратной матрицы
приходим к соотношению
 .
Откуда находим, что
.
Откуда находим, что
 ,
поскольку
,
поскольку
- определитель произведения квадратных матриц одинакового размера равен произведению определителей сомножителей;
- определитель матрицы не меняется при ее транспонировании;
-  .
.
Теорема доказана.
Теорема
11.4 Каждая
ортогональная матрица второго порядка
 ,
для которой
,
для которой
 может быть представлена в виде
может быть представлена в виде
 ,
где
,
где
 – некоторое число, а каждая ортогональная
матрица с
– некоторое число, а каждая ортогональная
матрица с
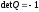 – в виде
– в виде
 .
.
Доказательство.
Пусть
матрица
 ортогональная, тогда должны быть
справедливы равенства
ортогональная, тогда должны быть
справедливы равенства

и, следовательно,
 .
.
Последнее матричное равенство может быть записано в виде системы скалярных уравнений
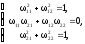
причем
из этих равенств, как было показано при
доказательстве теоремы 11.3, следует, что
 .
Рассмотрим случай
.
Рассмотрим случай
 .
.
Если
из суммы первого и третьего уравнений
системы вычесть удвоенное равенство
 ,
то мы получим
,
то мы получим

Или
 ,
,
откуда следует, что

Наконец,
из условий
 имеем оценки
имеем оценки
 ,
,
которые позволяют ввести обозначения
 ,
,
приводящие к требуемому виду матрицы Q поскольку из полученных соотношений также следует, что
 .
.
Случай
 рассматривается аналогично.
рассматривается аналогично.
Теорема доказана.
Следствие. Матрица перехода от одного ортонормированного базиса на плоскости к другому ортогональная .
Матрица S перехода от одной ортонормированной системы координат на плоскости к другой может иметь один из двух следующих видов:
 или
или
 ,
,
где
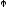 – угол между первыми базисными векторами.
Но тогда матрица перехода S
ортогональная в силу теоремы 11.4.
– угол между первыми базисными векторами.
Но тогда матрица перехода S
ортогональная в силу теоремы 11.4.
Следствие доказано.
