
- •I. Выборочный метод. Вариационные ряды. Построение эмпирической функции распределения, гистограммы частот
- •II. Статистические характеристики вариационных рядов. M(X), d(X), σ(X), Mo, Me, показатели вариации. Асимметрия и эксцесс.
- •III. Вычисление групповых и общих средних, групповой, внутригрупповой, межгрупповой дисперсии и общей дисперсии
- •IV. Доверительный интервал и доверительная вероятность (интервальное оценивание)
- •V.Сравнение двух дисперсий нормальных генеральных совокупностей
- •VI. Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки)
II. Статистические характеристики вариационных рядов. M(X), d(X), σ(X), Mo, Me, показатели вариации. Асимметрия и эксцесс.
Пусть для изучения генеральной совокупности относительно количественного признака извлечена выборка объема . Составлен интервальный вариационный ряд.
Выборочной
средней
![]() называют среднее арифметическое значение
признака выборочной совокупности.
называют среднее арифметическое значение
признака выборочной совокупности.
 , (6)
, (6)
где
![]() - представители интервалов (середины
интервалов),
- частоты соответствующих интервалов,
- объем выборки.
- представители интервалов (середины
интервалов),
- частоты соответствующих интервалов,
- объем выборки.
Выборочной
дисперсией
![]() называют среднее
арифметическое квадратов отклонения
наблюдаемых значений признака от их
среднего значения
называют среднее
арифметическое квадратов отклонения
наблюдаемых значений признака от их
среднего значения
![]() .
Для взвешенных вариантов формула
вычисления дисперсии имеет вид:
.
Для взвешенных вариантов формула
вычисления дисперсии имеет вид:
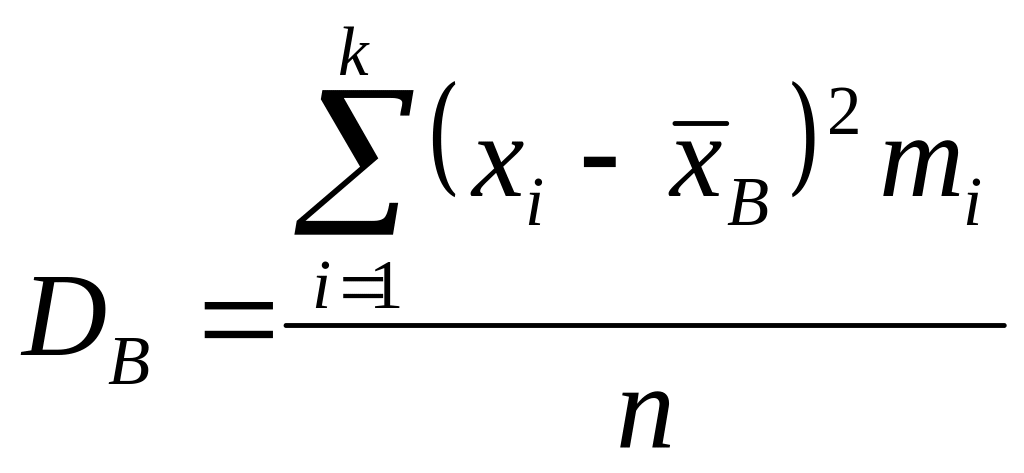 (7)
(7)
Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии:
![]() . (8)
. (8)
Среднее квадратическое
отклонение – это абсолютная мера
рассеяния вариантов ряда. Существует
и относительная мера рассеяния –
коэффициент вариации (![]() ).
).
Коэффициент вариации представляет собой процентное отношение среднего квадратического отклонения к средней выборочной:
![]()
![]() (9)
(9)
Если коэффициент вариации признака, принимающего только положительные значения, высок (например, более 100%), то это говорит о неоднородности значений признака.
Медиана
(![]() )
– значение признака ряда, относительного
которого вариационный ряд делится на
две равные по числу вариантов части.
)
– значение признака ряда, относительного
которого вариационный ряд делится на
две равные по числу вариантов части.
Для расчета значения медианы в интервальном вариационном ряду вначале находят интервал, содержащий медиану. Медианному интервалу соответствует первая из накопленных частот, превышающая половину всего объема совокупности. Расчет медианного интервала производят по формуле:
 , (10)
, (10)
где
![]() - нижняя граница медианного интервала,
- величина медианного интервала,
- нижняя граница медианного интервала,
- величина медианного интервала,
![]() - половина суммы всех частот,
- половина суммы всех частот,
![]() - накопленная частота интервала,
предшествующего медианному,
- накопленная частота интервала,
предшествующего медианному,
![]() - частота медианного интервала.
- частота медианного интервала.
Мода
(![]() )–
это значение признака, наиболее часто
встречающееся в вариационном ряду.
)–
это значение признака, наиболее часто
встречающееся в вариационном ряду.
В случае, если интервальный вариационный ряд имеет равные интервалы, то модальный (содержащий моду) интервал определяется по наибольшей частоте. Мода внутри модального интервала находится по следующей формуле:
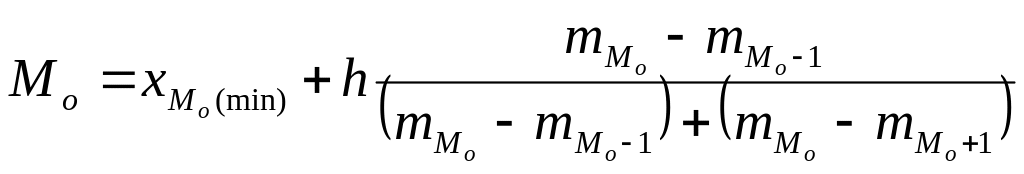 , (11)
, (11)
где
![]() - нижняя граница модального интервала,
- величина модального интервала,
- нижняя граница модального интервала,
- величина модального интервала,
![]() - частота модального интервала;
- частота модального интервала;
![]() - частота интервала, предшествующего
модальному (предмодального интервала),
- частота интервала, предшествующего
модальному (предмодального интервала),
![]() - частота интервала, следующего за
модальным (постмодального интервала).
- частота интервала, следующего за
модальным (постмодального интервала).
Центральным
эмпирическим моментом
![]() - го порядка
называется среднее арифметическое
-х
степеней отклонений наблюдаемых значений
случайной величины от их среднего
арифметического (
)
и обозначается
- го порядка
называется среднее арифметическое
-х
степеней отклонений наблюдаемых значений
случайной величины от их среднего
арифметического (
)
и обозначается
![]() ,
т.е.
,
т.е.
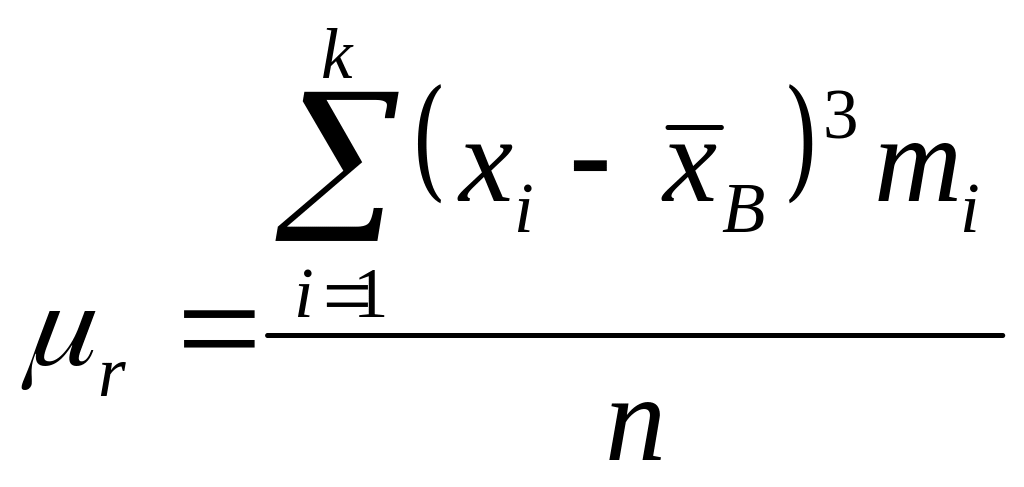 (12)
(12)
Вариационный ряд, в котором частоты вариантов, равноотстоящие от средней арифметической, равны между собой, называют симметричным, в противном случае – асимметричным, скошенным.
Необходимым, но не достаточным условием симметричности является равенство трех характеристик: средней арифметической, моды и медианы:
![]() .
.
Если более длинная часть графика распределения расположена правее от вершины, то имеет место правосторонняя скошенность, а если левее - левосторонняя скошенность.
Для оценки отклонения эмпирического распределения от нормального используют различные характеристики, к числу которых относятся асимметрия и эксцесс.
Асимметрия эмпирического распределения определяется равенством
![]() , (13)
, (13)
где
![]() - центральный
эмпирический момент третьего порядка.
- центральный
эмпирический момент третьего порядка.
Пределы значений
асимметрии от
![]() до
до
![]() .
.
При
![]() распределение
симметрично
распределение
симметрично
![]() .
.
При
![]()
![]() ,
т.е. распределение имеет правостороннюю
скошенность.
,
т.е. распределение имеет правостороннюю
скошенность.
При
![]()
![]() ,
т.е. распределение имеет левостороннюю
скошенность.
,
т.е. распределение имеет левостороннюю
скошенность.
Эксцесс эмпирического распределения определяется равенством
![]() , (14)
, (14)
где
![]() - центральный
эмпирический момент четвертого порядка.
- центральный
эмпирический момент четвертого порядка.
Значения коэффициента
эксцесса лежат на полусегменте
![]() .
.
Эксцесс является мерой «крутости» распределения (высоковершинности или низковершинности).
Если
![]() ,
то имеет место островершинность.
,
то имеет место островершинность.
Если
![]() ,
то распределение имеет плоскую вершину.
,
то распределение имеет плоскую вершину.
Вариационный ряд, в котором частоты вариантов, равноотстоящие от средней арифметической, равны между собой, называют симметричным, в противном случае – асимметричным, скошенным.
Пример 2. Вычислить числовые характеристики случайной величины (Таблица №1), асимметрию и эксцесс.
Решение.
Найдем объем выборки - n, наибольшее значение случайной величины -
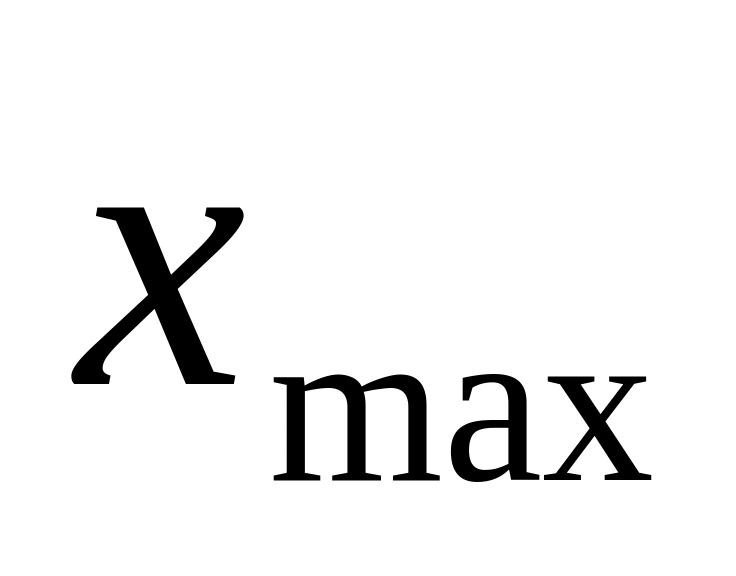 ,
наименьшее значение -
,
наименьшее значение -
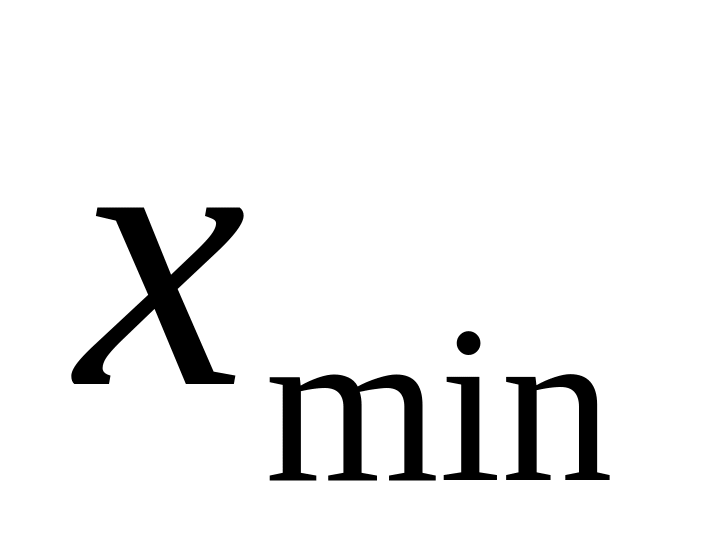 и шаг
.
Воспользуемся результатами расчетов
Л.Р. №1 (Таб.№2).
и шаг
.
Воспользуемся результатами расчетов
Л.Р. №1 (Таб.№2).Запишем интервальный ряд.
Найдем частоты, соответствующие каждому из полученных интервалов: Сервис \ Анализ данных \ Гистограмма и накопленные частоты.
Рассчитаем относительные частоты -
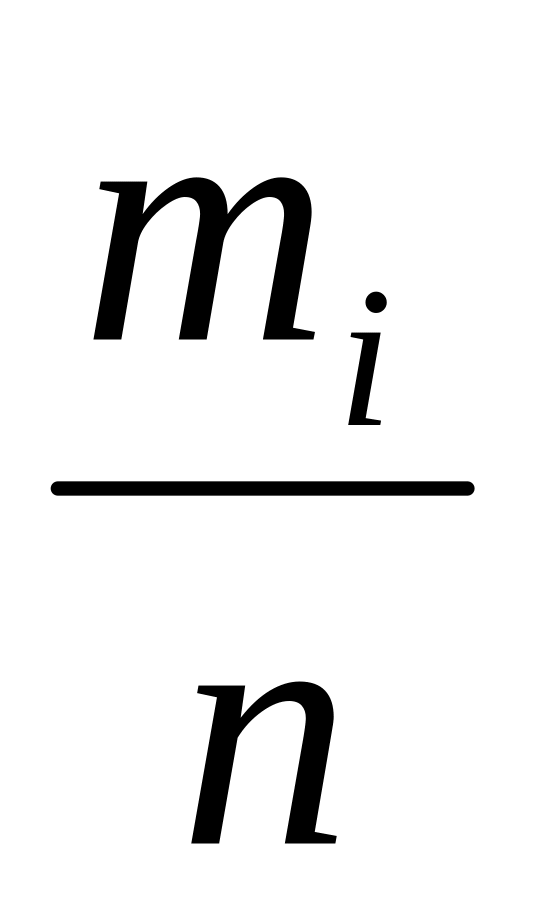 .
.Найдем середины интервалов - .
Найдем выборочную среднюю (формула (6)).
Вычислим выборочную дисперсию (смещенную оценку генеральной дисперсии) по формуле (7).
Вычислим выборочное среднее квадратическое отклонение (формула (8)).
Найдем центральные эмпирические моменты третьего -
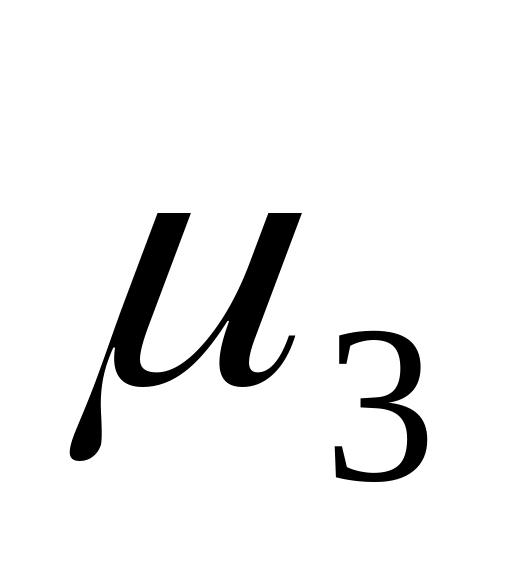 и четвертого -
и четвертого -
 порядков:
порядков:
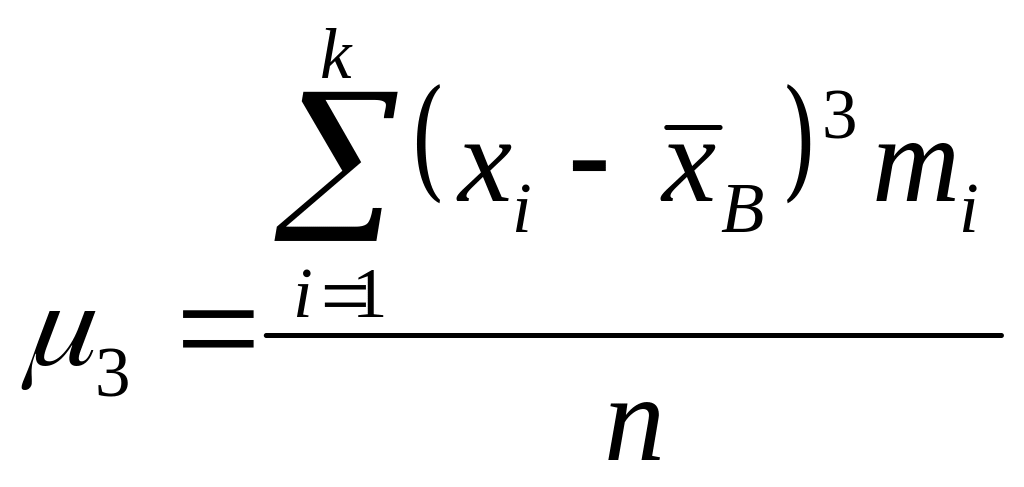 (15)
(15)
 (16)
(16)
Найдем асимметрию и эксцесс (формулы (11), (12), результаты указаны в расчетной таблице).
Найдем моду и медиану. Для расчета значения медианы в интервальном вариационном ряду вначале находим интервал, содержащий медиану. Таким интервалом является -
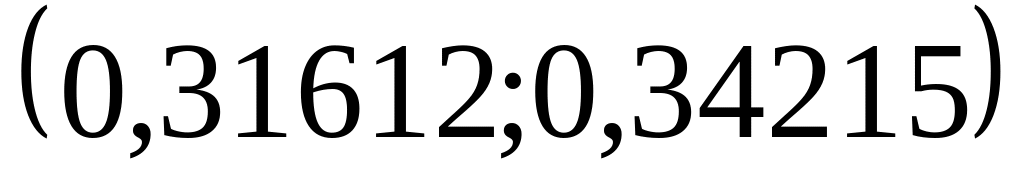 ,
т.к. ему соответствует первая из
накопленных частот (64), превышающая
половину всего объема (50) совокупности.
Расчет медианного интервала производим
по формуле (10):
,
т.к. ему соответствует первая из
накопленных частот (64), превышающая
половину всего объема (50) совокупности.
Расчет медианного интервала производим
по формуле (10):

Для
расчета моды определим сначала модальный
(содержащий моду) интервал. В данном
случае два интервала, которым соответствует
наибольшая частота:
и
![]() .
Моду внутри модальных интервалов
определяем по следующей формуле (11):
.
Моду внутри модальных интервалов
определяем по следующей формуле (11):

![]()
Таким
образом
![]() .
.
Этапы решения задачи оформим в виде расчетной таблицы (Таблица № 5). Все расчеты выполним в табличном процессоре Excel.
Таблица №5
Интервалы |
Карман |
Частота (mi) |
Отнсительная частота (mi/n) |
Накопленная относительная частота |
Накопленная частота |
|
|
|
|
|
|
|
|
||
a0 |
0,21198 |
0,21198 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
a1 |
0,23802 |
0,23802 |
3 |
0,03 |
0,03 |
3 |
0,22500 |
0,00675 |
0,0089798 |
0,0002694 |
-0,0008509 |
-0,000025528 |
0,000080637 |
0,000002419 |
|
a2 |
0,26405 |
0,26405 |
13 |
0,13 |
0,16 |
16 |
0,25103 |
0,03263 |
0,0047236 |
0,0006141 |
-0,0003246 |
-0,000042204 |
0,000022312 |
0,000002901 |
|
a3 |
0,29008 |
0,29008 |
15 |
0,15 |
0,31 |
31 |
0,27707 |
0,04156 |
0,0018229 |
0,0002734 |
-0,0000778 |
-0,000011674 |
0,000003323 |
0,000000498 |
|
a4 |
0,31612 |
0,31612 |
15 |
0,15 |
0,46 |
46 |
0,30310 |
0,04547 |
0,0002776 |
0,0000416 |
-0,0000046 |
-0,000000694 |
0,000000077 |
0,000000012 |
|
a5 |
0,34215 |
0,34215 |
18 |
0,18 |
0,64 |
64 |
0,32913 |
0,05924 |
0,0000878 |
0,0000158 |
0,0000008 |
0,000000148 |
0,000000008 |
0,000000001 |
|
a6 |
0,36818 |
0,36818 |
18 |
0,18 |
0,82 |
82 |
0,35517 |
0,06393 |
0,0012536 |
0,0002256 |
0,0000444 |
0,000007989 |
0,000001571 |
0,000000283 |
|
a7 |
0,39422 |
0,39422 |
13 |
0,13 |
0,95 |
95 |
0,38120 |
0,04956 |
0,0037748 |
0,0004907 |
0,0002319 |
0,000030149 |
0,000014249 |
0,000001852 |
|
a8 |
0,42025 |
0,42025 |
4 |
0,04 |
0,99 |
99 |
0,40723 |
0,01629 |
0,0076514 |
0,0003061 |
0,0006693 |
0,000026772 |
0,000058545 |
0,000002342 |
|
a9 |
0,44628 |
0,44628 |
1 |
0,01 |
1 |
100 |
0,43327 |
0,00433 |
0,0128836 |
0,0001288 |
0,0014624 |
0,000014624 |
0,000165988 |
0,000001660 |
|
|
|
n= |
100 |
|
|
|
|
0,31976 |
|
0,0023656 |
|
-0,000000418 |
|
0,000011968 |
|
|
|
|
|
|
|
|
|
|
|
0,0486374 |
|
|
|
|
|
Статистические характеристики. Показатели вариации. |
|||||||||||||||
Выборочная средняя |
0,31976 |
||||||||||||||
Выборочная дисперсия |
|
||||||||||||||
Выборочное среднее квадратическое отклонение |
|
||||||||||||||
Центральный момент третьего порядка |
|
||||||||||||||
Центральный момент четвертого порядка |
0,000000000 |
||||||||||||||
Асимметрия |
|
||||||||||||||
Эксцесс |
|
||||||||||||||
Мода |
|
||||||||||||||
Медиана |
|
||||||||||||||
Задача 2. Вычислить числовые характеристики случайной величины (Таблица №4), асимметрию и эксцесс. Результаты оформить в виде расчетной таблицы Excel.
