
РОССОБРАЗОВАНИЕ
Г осударственное
образовательное учреждение высшего
профессионального образования
осударственное
образовательное учреждение высшего
профессионального образования
Пензенская государственная технологическая академия

В.А.Авроров
ФИЗИКО-МЕХАНИЧЕСКИЕ СВОЙСТВА СЫРЬЯ И ГОТОВОЙ ПРОДУКЦИИ В ВОПРОСАХ И ОТВЕТАХ
Основные понятия Проблемы Задачи Методы Формулы
Пенза 2010
УДК 664.002.612
ББК
А
Рецензент:
Авроров В.А.
Физико-механические свойства сырья и готовой продукции в вопросах и ответах. – Пенза: ПГТА, 2010. - 167с.
ISBN
Методическая разработка составлена в соответствии с программой дисциплины «Физико-механические свойства сырья и готовой продукции», служит для глубокого понимания целей и задач дисциплины и более полного усвоения теоретического материала.
Для каждой темы курса подготовлены вопросы и ответы по основным понятиям и проблемам инженерной реологии, используемым методам и средствам (155 вопросов и ответов).
Данная методическая разработка вместе с рабочей тетрадью являются необходимым приложением к базовому курсу лекций и обязательному практикуму по лабораторным работам и в совокупности составляют учебно-методический комплекс дисциплины.
Для студентов, аспирантов и преподавателей по направлению подготовки дипломированных специалистов 260600 «Пищевая инженерия».
© ПГТА, 2010
Содержание
Введение
Тема 1. Основные понятия инженерной реологии
Тема 2. Реологические свойства пищевых продуктов
Тема 3. Моделирование реологического поведения пищевых материалов
Тема 4. Методы и средства измерения реологических свойств пищевых материалов
Тема 5. Особенности строения частиц сыпучих продуктов и их физико-механические свойства
Тема 6. Физико-механические свойства сырья, полуфабрикатов и готовой продукции
Введение
Обеспечение высокого качества пищевой продукции предприятиями АПК невозможно без знаний свойств и особенностей строения перерабатываемого сырья и полуфабрикатов, а также без учета особенностей взаимодействия пищевых материалов с рабочими органами машин.
Знание физико-механических и других характеристик сырья и полуфабрикатов, например, таких как плотность, вязкость, прочность, термовлагопроводность, податливость и др., и умение оценивать степень их влияния на выходные параметры готовой продукции и эксплуатационные показатели самого оборудования является исходной предпосылкой для создания совершенных конструкций машин и аппаратов пищевых производств.
Основная цель данной методической разработки – обеспечить путем формулирования вопросов и кратких ответов на них осознанное и глубокое понимание основного курса лекций по физико-механическим свойствам сырья и готовой продукции, их влиянии на технологию обработки и конструкцию исполнительных органов и рабочих зон машин и аппаратов, а также побудить студента к самостоятельной работе.
Тема 1. Основные понятия инженерной реологии
1.1.Основные положения механики сплошных сред
1.2.Цели и задачи инженерной реологии в пищевых производствах
1.3.Понятие о тензорах и тензорном исчислении
1.1 Основные положения механики сплошных сред |
|||||||||||||||||
Вопросы |
Ответы |
||||||||||||||||
1. Что является основой реологии?
|
В основе реологии, как науки о течениях и деформациях материалов, лежит классическая механика сплошных сред, основными задачами которой является изучение состояния и поведения различных материалов с геометрических (деформации), кинематических (скорости деформаций) и динамических (напряжения) позиций. |
||||||||||||||||
2. Что происходит внутри физического тела при приложении к нему внешней нагрузки
|
В процессе обработки пищевое сырье и полуфабрикаты подвергаются внешним механическим и другим видам воздействий, в результате которых внутри тел в любой их точке возникают динамические состояния, характеризуемые определенной физической величиной, называемой напряжением. Напряжения возникают только внутри вещества и обуславливаются силами, действующими в данный момент на тело. Кроме того, напряжения могут возникать внутри физических тел вследствие неоднородности температурного поля или как предыдущая «память» от термической или механической обработки материала.
|
||||||||||||||||
3. Что понимается под сплошной средой, и какими параметрами она может быть охарактеризована?
|
Многие материалы, используемые пищевой промышленностью для производства продуктов питания, могут рассматриваться в виде системы большого количества материальных точек и быть представлены моделями сплошной среды.
Для описания
состояний такой среды нужно знать
некоторые параметры распределения,
например, распределения плотности
материала по сплошной среде. Так,
средняя плотность
Аналогично,
средняя плотность распределения сил,
приложенных в точках сплошной среды
при ее обработке в рабочих зонах
технологического оборудования,
определится как отношение главного
вектора сил
Действия объемных сил, например, таких как, силы трения между слоями материала при его истирании или внешние силы, действующие на границе раздела сред, можно заменить действиями поверхностных сил, определяемых плотностью распределения по поверхности. В отличие от механики абсолютно твердого тела и механики дискретных материальных точек механика сплошных сред оперирует характеристиками векторного и тензорного исчисления. Считают, что в механике сплошных сред все рассматриваемые физические величины непрерывно распределены в пространстве, которое занимает сплошная среда и в каждой точке этого пространства однозначно определены значения физических величин.
|
||||||||||||||||
4. Как находятся главные векторы поверхностных сил, действующих на тело? |
Главные векторы
объемных и поверхностных сил, приложенные
к конечным объемам или площадям
поверхности, находятся суммированием
элементарных объемных или поверхностных
сил по объему
или поверхности
|
||||||||||||||||
5. Что понимается под напряжениями, возникающими в физических телах?
|
Механика сплошных сред рассматривает явления, происходящие внутри физических тел. Приложенные к телу силы создают динамическую ситуацию в любой точке тела, которая характеризуется напряжением.
Сила
Среднее напряжение
в материале
равно
Напряжения – это характеристики сил, действующих в определенной точке, интерпретируемые как относительные силы или силы, отнесенные к единице площади. |
||||||||||||||||
6. Каким методом находятся напряжения в физических телах? |
Напряжения в сплошной среде находятся методом сечений.
В общем случае
в сплошной среде можно в каждой ее
точке провести бесконечное множество
плоских сечений по-разному ориентированных
в пространстве. Отбросив с одной
стороны сечения сплошную среду и учтя
ее действие на оставшуюся часть, можно
найти поверхностную силу, приложенную
к сечению со стороны отброшенной
части. Отношение силы к площади сечения
даст плотность распределения
поверхностной силы по сечению или
напряжение в данной точке среды,
являющееся вектором. Ориентация
элементарной площади сечения
Выделим в сплошной
среде элемент в форме тетраэдра,
боковые грани которого лежат в
координатных плоскостях
Выделенный
элементарный объем тетраэдра
|
||||||||||||||||
7. На какие компоненты может быть разложен вектор силы, действующей на выделенной малой площадке тела?
|
Пусть необходимо
найти силу, действующую на поверхность
и имеющую наклон под произвольным
углом
Разложение силы
Сложим силы, действующие на призму.
Так,
На основание
призмы действует Х
- компонента
силы
Пусть
-
единичный вектор нормали к наклонной
грани призмы, а
Составляющая
напряжения по оси
Из рисунка видно,
что отношение
Обобщая полученный
результат на произвольный элемент
поверхности, получим
Формула показывает,
что можно выразить силу, действующую
на произвольную площадь, через
компоненты тензора
Поскольку численные значения компонент напряжения зависят от ориентации в пространстве площадки, на которой они действуют, то существует такая ориентация площадки, на которой напряжения будут иметь максимальное значение. Если рассечь тело плоскостью, расположенной под углом к горизонтальной оси, то сила растяжения, приложенная к телу по его оси, разложится на две составляющие – нормальную (перпендикулярно плоскости сечения) и тангенциальную (лежащую в плоскости сечения). Поскольку компоненты тензора напряжений равны отношению силы к площади, на которой они действуют, то можно записать:
|
||||||||||||||||
8. Какой величиной определяется ориентация в пространстве площадки, к которой приложена действующая сила?
|
Ориентация площадок задается вектором нормали к ней, который также раскладывается на компоненты по координатным осям. Поскольку ориентация площадок в пространстве, относительно которых будут рассматриваться внутренние силы, может быть разной, то и действующие на них силы будут разными, что свидетельствует о тензорной природе возникающих внутренних напряжений в теле от действия на него нагрузок.
Если сделать
разрез в теле перпендикулярно оси
,
разложить действующую в разрезе силу
Разложение действующей силы на три составляющие на элементарной площадке ортогональной к оси
Если сделать разрез перпендикулярно оси то соответственно получим еще три компоненты:
Аналогичным
образом находятся три компоненты на
площадке ортогональной оси
:
Разложение действующей силы на три составляющие на элементарной площадке ортогональной к оси
|
||||||||||||||||
9. Что понимается под деформацией тела? |
Любое внешнее воздействие на физическое тело приводит или к его смещению, или к изменению его первоначальной формы, или к суммарному действию этих эффектов. Классическая механика занимается изучением движения тел, которые происходят без изменения их формы, механика сплошных сред изучает внутренние состояния этих тел, инженерная реология занимается свойствами пищевых материалов, которые определяются соотношениями между напряжениями и деформациями. Изменение формы, т.е. изменение расстояний между различными точками в объеме тела, собственно и является деформацией тела.
Если взять внутри
элементарного единичного кубика,
находящегося в состоянии равновесия,
какую-то материальную точку
В области упругих
деформаций величина перемещения
материальной точки с координатой
Однородная деформация растяжения
|
||||||||||||||||
1.2.Цели и задачи инженерной реологии в пищевых производствах |
|||||||||||||||||
10. Что понимается под инженерной реологией и каково ее основное назначение как науки? |
Инженерная реология - наука о деформации и течении различных тел, исследующая способы определения структурно-механических свойств сырья, полуфабрикатов и готовых продуктов с помощью соответствующего приборного оснащения с целью использования полученных результатов для совершенствования технологических процессов и повышения качества на всех стадиях производства готовой пищевой продукции. Основное назначение инженерной реологии, как науки, состоит в определении свойств сырья и продуктов для использования их в качестве нормативов в технологической документации и в получении необходимых данных для расчета конструктивно-технологических параметров технологического оборудования.
|
||||||||||||||||
11. Какие процессы исследуют, и какие показатели определяют методами инженерной реологии в пищевой промышленности, и с какой целью? |
Методами инженерной реологии на основе биохимических, биофизических, физико-химических и органолептических показателей проводят исследование процессов структурообразования продуктов, определяют нормативные показатели структурно-механических свойств продуктов для использования в технологической документации, получают необходимые данные для проектирования и расчета технологического оборудования. Протекание различных процессов: механических, тепловых, диффузионных, электрических и др. в значительной степени определяется структурно-механическими свойствами продуктов, которые зависят от внутреннего строения и состава продукта, характера взаимодействия между собой частиц или молекул, физико-химического состояния влаги в материале и других факторов, определяющих тип структуры.
|
||||||||||||||||
12. Каким образом выражают свойства и поведение тел при проведении исследований методами инженерной реологии? |
При проведении реологических исследований свойства и поведение реальных тел выражают в виде математических или механических моделей, которые с теми или иными допущениями характеризуют параметры их изменения в процессе обработки. Пищевые продукты, большинство из которых относится к сложным дисперсным системам, характеризуются определенными физико-химическими свойствами, среди которых важнейшее место занимают реологические свойства. Развитие реологии, как составной части механики сплошных сред и как науки о течении и деформации тел, способствовало созданию и применению новых методов анализа процессов переработки пищевых масс и способов получения продуктов с задаваемыми свойствами, а также новых подходов при проектировании технологического оборудования пищевых производств. Прогнозирование поведения пищевых масс при их обработке в технологических потоках требует определения количественных характеристик реологических свойств, таких как прочность, упругость, пластичность, вязкость и др., что целесообразно проводить на базе теории упругости, вязкоупругости, вязкопластичности и др. с применением известных реологических моделей или созданием новых их комбинаций.
|
||||||||||||||||
13. Каковы основные задачи инженерной реологии в пищевой промышленности? |
К основным задачам реологии в пищевой промышленности относятся: - определение реологических характеристик продуктов при различных значениях технологических факторов; - создание средств технического оснащения для изучения деформирования реальных продуктов; - разработка обоснованных методов расчета технологических процессов и технических систем; - управление структурными свойствами и качеством продукции
|
||||||||||||||||
14. В какие группы в зависимости от действующих усилий и возникающих от них в обрабатываемых материалах напряжений объединяются реологические свойства материалов? |
Реологические свойства продукции характеризуют ее поведение в условиях напряженного состояния при воздействии внешней нагрузки, которая приводит к смещениям тел и деформациям материала в рабочих зонах машин. Это поведение зависит от формы и размеров тела, скорости деформации, структуры продукта, температуры, давления и других факторов. В зависимости от действующих усилий и возникающих от них в обрабатываемых материалах напряжений реологические свойства объединяются в три основные группы: - сдвиговые свойства, характеризующие поведение продукта при действии касательных напряжений; - компрессионные свойства, характеризующие поведение продукта при действии усилий сжатия; - поверхностные свойства, возникающие на гранях раздела сред при воздействии нормальных и касательных напряжений.
|
||||||||||||||||
15. Какие показатели определяются при изучении компрессионных свойств пищевых материалов? |
Определение упругопластических показателей, закономерностей изменения плотности от давления, характеристик ползучести и релаксации напряжений составляет предмет исследований при изучении компрессионных свойств.
|
||||||||||||||||
16. Какие зависимости определяют при построении реологических моделей тел и их сдвиговых характеристик? |
Для выявления сдвиговых характеристик и определения типа реологической модели проводят анализ зависимостей величины касательных напряжений от скоростей сдвига (кривых течения).
|
||||||||||||||||
17. Какие оценки необходимо получить при исследовании поверхностных свойств пищевых материалов? |
Оценки адгезионных и фрикционных характеристик продуктов, зависимостей адгезионного давления от величины напряжения, скорости отрыва получают при изучении поверхностных свойств. Фрикционные показатели оценивают по статическим и динамическим коэффициентам трения.
|
||||||||||||||||
1.3.Понятие о тензорах и тензорном исчислении |
|||||||||||||||||
18. Что понимается под полем физической величины? |
Совокупность значений физических величин, соответствующая точкам пространства, определяет поле этих величин. Это поле задается функциями координат в области определения физической величины при ограничениях непрерывности и существования производных по координатам.
Если каждой точке
пространства
ставится в соответствие какая-то
скалярная величина
|
||||||||||||||||
19. Что понимается под градиентом скалярного поля? |
Градиент скаляра
Градиентом
скалярного поля
|
||||||||||||||||
20. Каким образом вводится понятие векторного поля? |
Если каждой точке
пространства ставится в соответствие
вектор
Если для векторного
поля
существует функция
такая, что
Если рассматривается поле векторной величины, то проекции вектора на оси координат зависят от выбора этих осей в пространстве, но длина вектора при этом является инвариантной. |
||||||||||||||||
21. Что называется векторной суммой двух векторов |
Векторная сумма
|
||||||||||||||||
22. Что представляет собой произведение вектора на скаляр (действительное число) ? |
Произведение
вектора
на скаляр
есть вектор, соответствующий
направленному отрезку в
|
||||||||||||||||
23. Каким образом задается вектор в декартовой прямоугольной системе координат? |
Если в пространстве
задана правая прямоугольная система
декартовых координат, то единичные
векторы
осей
Координаты
|
||||||||||||||||
24. Чему равно скалярное произведение векторов и ? |
Скалярное
(внутреннее) произведение векторов
и
обозначается
|
||||||||||||||||
25. Чему равно векторное произведение двух векторов? |
Векторное
произведение
Его направление
перпендикулярно к обоим векторам
и
и совпадает с направлением поступательного
движения правого винта при его повороте
от
к
на
угол меньший
|
||||||||||||||||
26. В каком случае два вектора будут линейно зависимы? |
Два вектора линейно зависимы тогда и только тогда, когда их векторное произведение равно нулю. |
||||||||||||||||
27. Что понимается под дивергенцией векторной функции точки? |
Дивергенция
векторной функции точки
Дивергенцией
Дивергенция некоторого вектора определяется пределом отношения векторного потока через малую замкнутую поверхность, окружающую какую-либо точку расхождения или схождения этого потока, к объему, ограниченному той же малой поверхностью (мощность источника) |
||||||||||||||||
28. Что понимается под ротором векторной функции точки? |
Ротор векторной
функции точки
есть векторная функция точки,
определяемая формулой
Ротор (вихрь)
векторного поля
Наглядно понятие
ротора вводится с помощью понятия
циркуляции
векторного поля
вдоль замкнутой кривой
Ротор некоторого вектора определяется как предел отношения наибольшей циркуляции вокруг малой замкнутой поверхности, окружающей какую-либо точку, к величине площади этой поверхности |
||||||||||||||||
29. Каково координатное представление ротора? |
Координатное представление ротора задается следующей формулой:
Если в произвольном
поле скоростей
Циркуляция векторного поля |
||||||||||||||||
30. В чем сущность теоремы о дивергенции (теоремы Гаусса-Остроградского)? |
Теорема о дивергенции связывает объемные интегралы по области и поверхностные интегралы по границе этой области. Область предполагается ограниченной и пространственно односвязной, поверхность - замкнутой и регулярной. Область в евклидовом трехмерном пространстве называется пространственно-односвязной, если любую простую замкнутую поверхность типа сферы, лежащую в , можно с помощью непрерывной деформации стянуть в точку, не выходя из . Регулярной поверхностью называется двухсторонняя простая (замкнутая или незамкнутая) поверхность, составленная из конечного числа регулярных кусков с общими регулярными дугами и точками.
Точка поверхности
называется регулярной точкой, если
при некотором параметрическом задании
поверхности функции
Формулировка теоремы о дивергенции: поток вектора через замкнутую поверхность равен интегралу от дивергенции по объему, ограниченному этой поверхностью.
|
||||||||||||||||
31. В чем сущность теоремы о роторе (теоремы Стокса)? |
Если векторная
функция
однозначна и имеет непрерывные частные
производные всюду в конечной
поверхностно-односвязной области
и если лежащая в области
поверхность
односвязна, регулярна и ограничена
регулярной замкнутой кривой
|
||||||||||||||||
32. Каким образом вводится формальное понятие тензора? |
В статике и
кинематике сплошной среды встречаются
задачи, когда требуется перейти от
одного вектора к другому. Этот переход
может задаваться линейным преобразованием
Пусть имеются
два вектора
Пусть
три единичных вектора правой декартовой
системы координат, причем
Если положить
Таким образом, если описание какого-либо объекта (математического или физического) потребует идентификации двух векторов, то объекты, определяемые с помощью этих векторов, называются тензорами.
|
||||||||||||||||
33. Почему напряжения, возникающие в материале, представляют собой тензорную величину? |
Представим себе
кусок материала, в сечении которого
действует поверхностная сила
.
Эта сила приложена к малой площадке
Можно видеть, что напряжение является результатом комбинации двух векторов и , определенных для какой-то конкретной точки. Величины напряжений зависят от направления приложения силы и ориентации площадки, на которой действуют эти силы, т.е. являются объектами тензорной природы. На практике удобней оперировать не с самими векторами, а с их проекциями на координатные оси. Каждый из векторов имеет по три проекции на ортогональные координатные оси:
Т.е. необходимо нужно определять девять величин: три проекции силы на площадку, зависящие от выбора трех координат, характеризующих положение этой площадке.
Так как величина
площадки, на которой действует сила,
несущественна, все три компоненты
силы
Тензор напряжений в компонентах
Таким образом, можно дать следующее определение тензора напряжений: тензор напряжений – это физический объект, связывающий два вектора - силу и нормаль к площадке, определяющей ее ориентацию в пространстве, т.е. это функция от направления и величины приложенной силы и плоскости, на которой действует эта сила.
Модель трехмерного напряженного состояния
Тензор
Компоненты
тензора напряжений с разными индексами
Компоненты с
одинаковыми индексами
Для симметричного
тензора полное описание внутренних
сил в произвольном твердом теле
потребует знания шести функций
координат
|
||||||||||||||||
34. Что понимается под главными напряжениями? |
Поскольку численные значения компонент напряжения зависят от ориентации в пространстве площадки, на которой они действуют, то существует такая ориентация площадки, на которой напряжения будут иметь максимальное значение. Если рассечь тело плоскостью, расположенной под углом к горизонтальной оси, то сила растяжения, приложенная к телу по его оси, разложится на две составляющие – нормальную (перпендикулярно плоскости сечения) и тангенциальную (лежащую в плоскости сечения). Поскольку компоненты тензора напряжений равны отношению силы к площади, на которой они действуют, то можно записать: - нормальное напряжение, - касательное напряжение.
При
Нормальные напряжения будут максимальны тогда, когда будут отсутствовать касательные напряжения, в этом случае они называются главными напряжениями. |
||||||||||||||||
35. Что понимается под инвариантами тензора? |
Для любого произвольного тензора существуют три независимые комбинации компонент, независящие от ориентации координатных осей в пространстве, которые называются инвариантами. Независимость главных напряжений и инвариантов тензора напряжений от выбора координатных осей характеризует тензор напряжений как физический объект, не связанный с какой-то координатной системой. |
||||||||||||||||
36. Что понимается под сферическим тензором и девиатором? |
Поскольку нормальные напряжения действуют перпендикулярно плоскостям элементарного единичного кубика. Выделенного из среды, а касательные напряжения действуют в плоскостях этого кубика, то, очевидно, действие нормальных напряжений приводит к изменению объема тела, а действие касательных напряжений – к изменению его формы.
Если элементарный
кубик поместить в жидкость, то он
подвергнется действию всестороннего
давления
Отсюда следует,
что главные напряжения равны между
собой
Давление выражается
как
Для плоского
напряженного состояния, например,
можно записать
Отсюда следует
тот факт, что у произвольного тензора
напряжений можно выделить гидростатическую
компоненту, в оставшейся части тензора
все касательные напряжения остаются
неизменными, а каждый диагональный
компонент становится равным
|
||||||||||||||||
37. Чему равны сферическая и девиаторная части тензора напряжений при одноосном растяжении тела? |
Тензор напряжения
при одноосном растяжении
Разделим данный тензор на гидростатическую и девиаторную компоненты и выделим гидростатическое давление и оставшуюся часть – разность между полным тензором и гидростатическим давлением, т.е. девиатор.
Каждая компонента полного тензора равна сумме компонент обеих составляющих с теми же индексами
Одноосное растяжение обязательно приводит к появлению девиаторной части тензора напряжений, это означает, что при одноосном растяжении в теле возникают касательные напряжения и тело не только растягивается вдоль направления действия силы, но и сжимается в поперечном направлении, т.е. меняется форма тела. |
||||||||||||||||
38. Что понимается под тензором деформации? |
а)
б) Однородная деформация сдвига (а) и однородный поворот без деформации (б)
При неоднородной
деформации в теле связь между
и
будет меняться от точки к точке. В этом
случае
Кроме сил
растяжения на кубик могут действовать
тангенциальные силы, ведущие к
деформации сдвига. В результате их
действия кубик изменит свою форму и
превратится в параллелограмм Полный
угол сдвига будет равен сумме углов
относительно осей
и
,
поскольку тангенциально приложенная
сила вызывает деформацию кубика
одновременно по двум осям, а не простое
его вращение в пространстве относительно
какой-то точки. Так, перемещение по
направлению оси
каждой материальной точки будет
пропорционально ее координате
Таким образом,
деформация сдвига выразится, как
В общем случае деформационное состояние тела, испытывающего воздействие растягивающих или сжимающих усилий и сдвиг, деформационное состояние определится заданием девяти чисел, являющихся компонентами тензора деформации.
При однородной
деформации, включая как растяжения,
так и сдвиги, все
При неоднородной
деформации могут возникнуть
дополнительные повороты тела.
При симметричном
тензоре деформации
Тензор деформации может быть разделен на две составляющие: сферическую, отвечающую за изменение объема тела, и девиаторную, выражающую изменение формы тела |
||||||||||||||||
39. Что понимается под главными значениями тензора деформации? |
Главные значения тензора деформации – это относительные удлинения вдоль трех прямоугольных координатных осей. Инварианты тензора представляют собой комбинации компонент, которые не зависят от выбора осей. Деформация наглядно может быть представлена превращением сферы в эллипсоид, когда радиусы шара по всем трем координатам изменяются по длине
Первый инвариант
тензора деформации означает, что
относительное изменение объема равно
этому инварианту
Относительное
изменение объема может быть выражено
через степени растяжения
|
||||||||||||||||
40. Какими показателями характеризуется кинематика относительного перемещения точек сплошной среды? |
Кинематика относительного перемещения точек сплошной среды характеризуется скоростью равной производной смещения точки по времени, градиентом скорости – производной по времени относительного смещения и скоростью деформации – производной по времени деформации. Градиент скорости представляет собой сумму двух компонент – скорости деформации и тензора скорости вращения, описывающего вращение элементов тела. Это вращение происходит одновременно с деформацией из-за смещения точек в пространстве. Известно, что движение материальной точки, так и физического тела, характеризуется скоростью, являющейся векторной величиной. Деформация движущегося тела проявляется в том случае, когда имеется градиент скорости, т.е. когда соседние точки, находящиеся на бесконечно малом расстоянии друг от друга, движутся с разными скоростями
Поскольку
пространственные координаты
материальной точки задаются ее
радиус-вектором
,
то компоненты градиента скорости
выражаются как
Можно записать
За деформацию тела ответственна симметричная часть градиента смещения.
Разложение
тензора
где
|
||||||||||||||||
41. Что представляет собой тензор упругости? |
Этот тензор связывает деформацию с напряжением в упругих телах, для которых справедлив закон Гука для любой материальной точки среды, т.е. когда напряжения в среде пропорциональны деформациям.
У тензора
напряжения
каждая i-я
компонента силы, действующей на
единичной площадке, перпендикулярной
оси
Поскольку
коэффициенты
и - это симметричные тензоры, содержащие по 6 компонент, то тензор будет включать 36 компонент, а при изотропном материале и еще меньше.
Общим уравнением,
связывающим
и
для изотропного материала, является
выражение
Коэффициенты
тензора упругости могут быть выражены
как через упругие постоянные Лямэ,
так и через модуль упругости материала
Например,
|
||||||||||||||||
42. Как преобразуются скаляры, векторы и тензоры при действии трехмерных дифференциальных операторов?
|
Скаляр
Вектор
Тензор
Скаляр
Вектор
Тензор
|
||||||||||||||||








 или
или


 или
или
 .
. ,
где через
,
где через


 .
.
 или
или
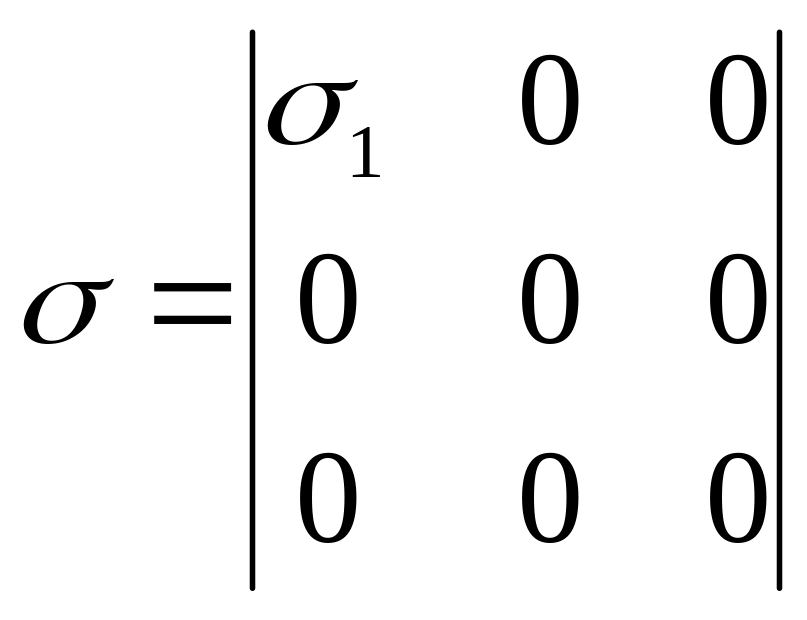 соответствует ситуации, когда все
силы кроме нормальной силы отсутствуют,
поэтому
соответствует ситуации, когда все
силы кроме нормальной силы отсутствуют,
поэтому



 ,
где
,
где
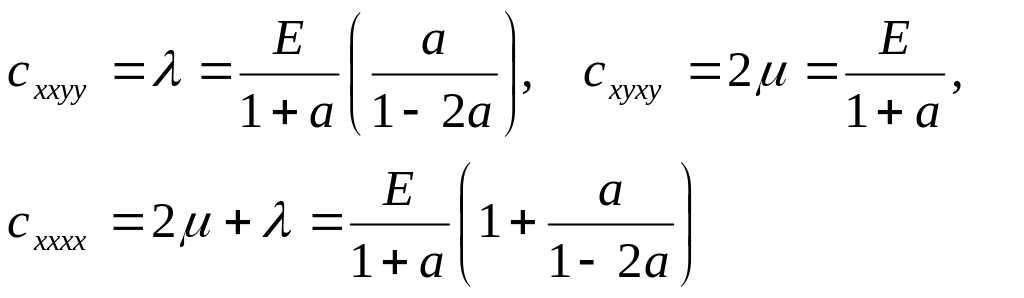 .
.