1.4.13. Розподіл Парето
Розподілом Парето називається розподіл випадкової величини, щільність розподілу якої має вигляд
(1.57)
Математичне сподівання, дисперсія, мода і медіана дорівнюють:
,
Графік розподілу
Парето для різних значень параметрів
і
наведений на рис. 1.13.
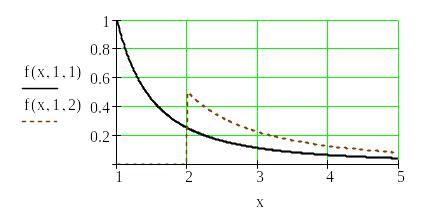
Рис. 1.13. Щільність розподілу Парето
Розподіл Парето
належить до так званих “зрізаних”
розподілів. Такі розподіли описують
імовірнісні закономірності у неповних
генеральних сукупностях, тобто у таких
сукупностях, із яких заздалегідь вилучені
усі елементи зі значеннями, які перевищують
або менше деякого заданого рівня
Розподіл Парето
широко застосовується в економічних
дослідженнях. Наприклад, при дослідженні
розподілу доходів осіб, річний доход
яких перевищує деякий заданий рівень
встановлений законом про податки.
1.5. Багатовимірні випадкові величини
Часто
результати випробувань характеризуються
не однією випадковою величиною, а деякою
системою випадкових величин
,
яку називають багатовимірною
(n
– вимірною) випадковою величиною
або випадковим
вектором
Випадкові величини, які входять у систему, можуть бути як дискретними, так і неперервними.
Імовірнісною характеристикою багатовимірної випадкової величини є її закон розподілу.
Дискретний
багатовимірний розподіл
задається
скінченим або зліченим набором значень
і ймовірностями цих значень
,
таких, що
Імовірність
визначається у цьому випадку як
При скінченій множині можливих значень багатовимірної випадкової величини, такий закон може бути заданий у формі таблиці (матриці), яка вміщує усілякі сполучення значень кожної із одновимірних складових двовимірної випадкової величини, які входять у систему, і відповідні їм імовірності. Для двовимірної дискретної величини (X, Y) закон розподілу можна представити у вигляді таблиці (матриці) розподілу, у кожній клітинці (i, j) якої стоять ймовірності
(1.58)
Функцією
розподілу
вимірної
випадкової величини
називається функція
яка виражає імовірність сумісного
виконання нерівностей
тобто
У двовимірному
випадку для випадкової величини
функція розподілу
визначається рівністю
(1.59)
Для дискретної двовимірної випадкової величини її функція розподілу визначається за формулою:
(1.60)
Властивості функції розподілу двовимірної випадкової величини аналогічні властивостям функції розподілу одновимірної випадкової величини:
Функція розподілу
однозначно
визначає ймовірності
для будь-яких паралелепіпедів
а отже, і для досить широкого класу
підмножин
Так при
.
(1.61)
Другий частинний випадок дають розподіли із щільністю розподілу.
Багатовимірною
(
вимірною)
щільністю розподілу
називається
така функція
,
що функція розподілу
може бути
представлена у вигляді
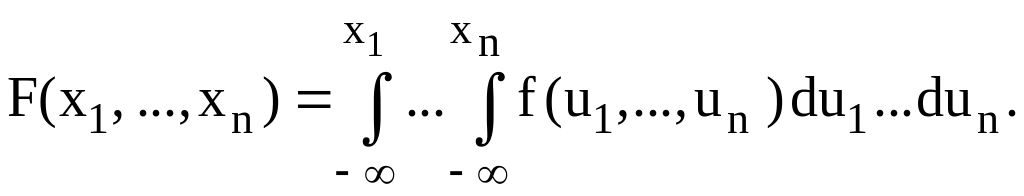(1.62)
Із (1.62) випливає, що у всіх точках неперервності підінтегральної функції її можна представити так:
(1.63)
Знаючи щільність
розподілу ймовірностей двовимірної
випадкової величини
,
можна знайти функції розподілу та
щільності розподілу ймовірностей її
одновимірних складових
Відповідні щільності
розподілу ймовірностей одновимірних
випадкових величин
(маргінальні щільності) мають вигляд:
(1.64)
Імовірність
попадання неперервної випадкової
двовимірної величини
в область
дорівнює
(1.65)
Зауважимо, що за відомими щільностями ймовірностей чи функціями розподілу компонент випадкового вектора, в загальному випадку, неможливо відтворити багатовимірну щільність або функцію розподілу випадкового вектора. Якщо випадкові величини, які утворюють систему, залежні, то для знаходження закону розподілу системи недостатньо знати закони розподілу окремих величин, які входять у систему (маргінальні розподіли). Потрібно ще знати умовні закони розподілу цих величин.
Умовним
законом розподілу однієї із
складових двовимірної випадкової
величини
називається її закон розподілу, обчислений
за умови, що друга складова прийняла
певне значення (або попала у деякий
інтервал).
У випадку довільного
типу випадкових величин (дискретних
або неперервних) функція розподілу
системи залежних випадкових величин
може бути записана у вигляді
(1.66)
де
умовні
функції розподілу випадкових величин
Для випадку системи
двох дискретних випадкових величин
умовні розподіли мають вигляд:
,
(1.67)
де
– одновимірні
(маргінальні) розподіли випадкових
величин
і
.
Умовні закони розподілу одновимірних складових двовимірної неперервної випадкової величини визначаються аналогічно умовним законам розподілу дискретних випадкових величин:
(1.68)
де
Попередні співвідношення, записані у вигляді
(1.69)
називаються формулою (правилом) множення щільностей розподілів.
При
вивченні двовимірних випадкових величин
розглядаються числові характеристики
одновимірних складових
математичні сподівання і дисперсії.
Для неперервної випадкової величини
вони визначаються за формулами:
,
(1.70)
(1.71)
Поряд з ними
розглядаються також числові характеристики
умовних розподілів: умовні математичні
сподівання
й умовні дисперсії
Ці характеристики знаходяться за
звичайними формулами математичного
сподівання і дисперсії, у яких замість
імовірностей
або щільностей імовірностей
використовуються умовні ймовірності
або умовні щільності ймовірностей
У загальному випадку одновимірні закони розподілу не визначають багатовимірні розподіли. Однак у важливому випадку незалежних випадкових величин за одномірними законами розподілу однозначно визначаються багатовимірні розподіли.
Випадкові
величини
називаються незалежними,
якщо для будь-яких дійсних
їх сумісна функція розподілу
представляється у вигляді добутку
функцій розподілу
цих випадкових величин:
(1.72)
У протилежному випадку (при невиконанні наведеної рівності) випадкові величини називаються залежними.
Часто зручніше
використовувати таке еквівалентне
означення незалежності: для будь-яких
подій
де
підмножини числової прямої, має місце
рівність
(1.73)
Диференціюючи рівність (1.73) по аргументах , одержимо
(1.74)
Це
означає, що для незалежних неперервних
випадкових величин
їх сумісна щільність
дорівнює добутку щільностей ймовірностей
цих випадкових величин. Таким чином,
незалежність, наприклад, двох випадкових
величин
і
означає, що умовні щільності ймовірностей
кожної із них співпадають із відповідними
безумовними щільностями:
(1.75)