4.2. Однородные дифференциальные уравнения 1 порядка

Функция называется однородной функцией n-го измерения относительно переменных x и y, если при любом t справедливо тождество

.

Например: – однородная функция третьего измерения относительно переменных x и y, так как

.

Функция является однородной функцией нулевого измерения, так как . Функция однородной не является, так как для нее условие не выполняется ни при каком n.

Дифференциальное уравнение в нормальной форме называется однородным дифференциальным уравнением 1-го порядка относительно переменных x и y, если – однородная функция нулевого измерения.

Дифференциальное уравнение в дифференциальной форме

называется однородным дифференциальным уравнением 1-го порядка, если функции и – однородные функции одного и того же измерения. При помощи подстановки , где – неизвестная функция, однородное уравнение преобразуется в уравнение с разделяющимися переменными.

Пример 4.2. Решить дифференциальное уравнение

.

Решение. Это – однородное уравнение, так как – одно-родная функция нулевого измерения. Положим .

Тогда .

– уравнение с разделенными переменными. Интегрируя, получим

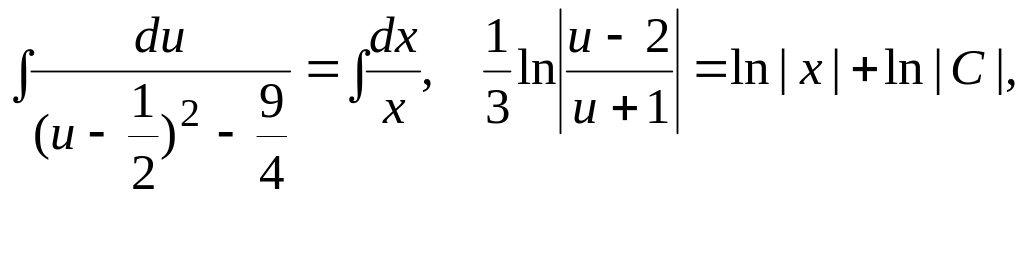
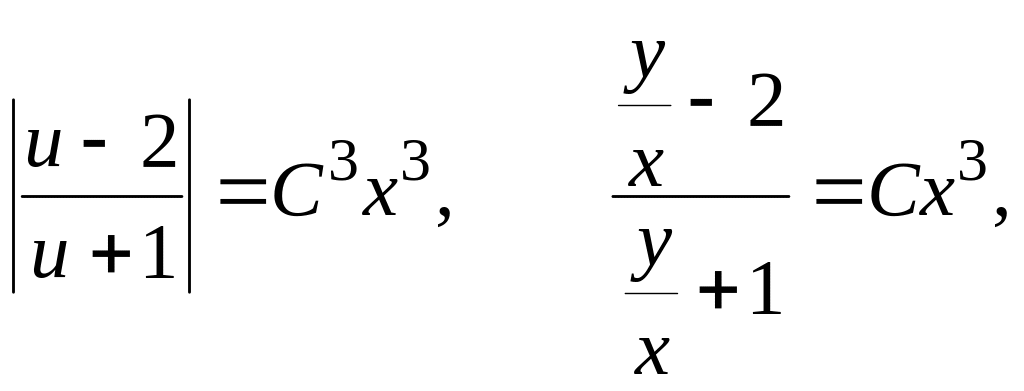
общий интеграл данного уравнения. Разрешив последнее равенство относительно y, получим общее решение .

Пример 4.3. Найти частное решение уравнения , удовлетворяющее начальному условию .

Решение. – однородные функции второго измерения. Подстановка приводит уравнение к виду

.

Интегрируя, получим

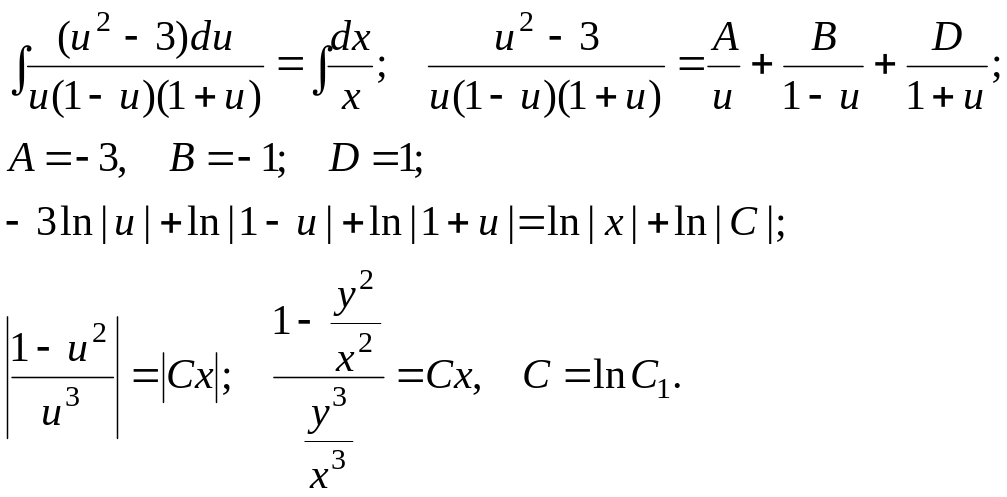
– общий интеграл данного уравнения. Найдем частный интеграл, удовлетворяющий условию

– частное решение уравнения.

4.3. Линейные дифференциальные уравнения 1-го порядка

_{Линейные дифференциальные уравнения 1-го порядка в общем виде можно записать соотношением}

_,

_{где P(x), Q(x) заданные непрерывные функции.}

Линейное уравнение можно решать с помощью замены

,

где и – неизвестные функции.

Тогда и уравнение примет вид

(4.1)

Функцию v(х) подбираем так, чтобы выражение в скобках было равно нулю, то есть в качестве v(х) возьмем одно из частных решений уравнения

.

Подставив выражение в уравнение (4.1), получаем уравнение с разделяющимися переменными

.

Найдя общее решение этого уравнения в виде , получим общее решение первого уравнения из подпункта 4.1 .

Пример 4.4. Найти общее решение уравнения

.

Полагаем , тогда и данное уравнение примет вид

Решая уравнение , найдем одно из его частных решений

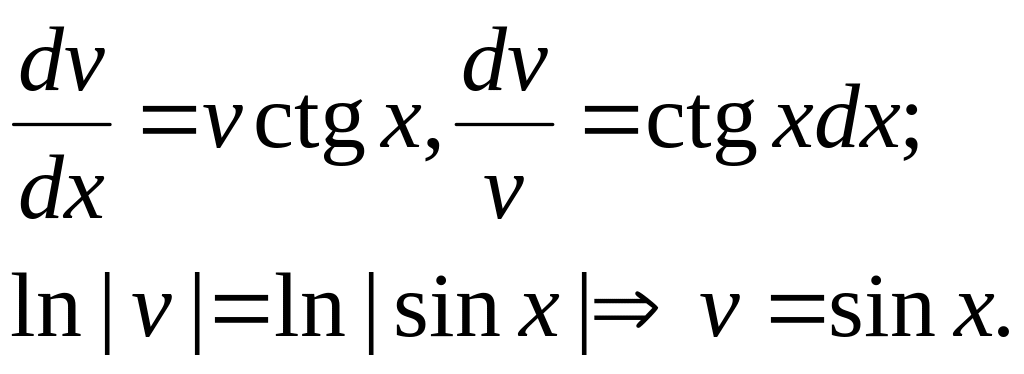
Подставляя v в уравнение (4.2), получим

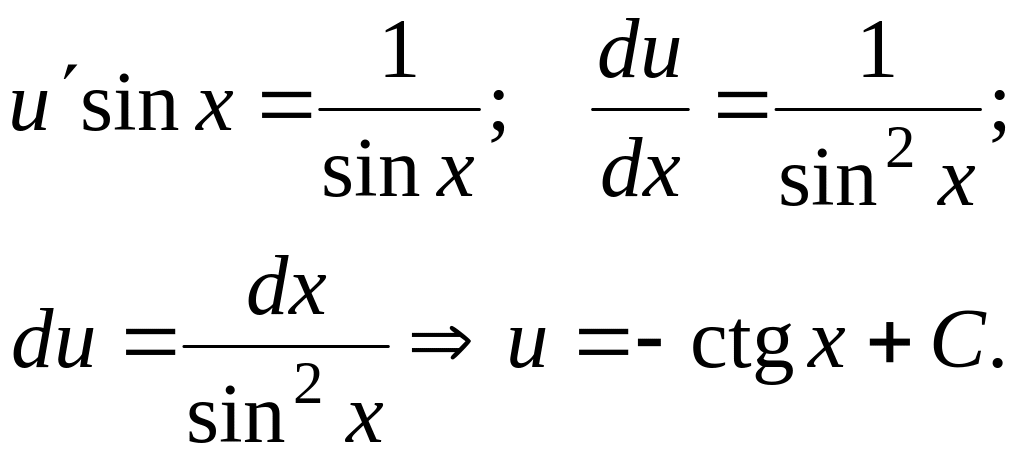
Общее решение исходного уравнения таково:

.

4.4. Уравнения Бернулли

Уравнения Бернулли имеют вид

,

где .

Такие уравнения можно проинтегрировать с помощью подстановки или свести к линейным уравнениям с помощью замены .

Пример 4.5. Решить уравнение .

Полагая , приводим уравнение к виду

. (4.3)

Уравнение имеет частное решение .

Подставляя u в уравнение (4.3), получаем уравнение

.

Его общее решение . Общее решение исходного уравнения:

.

Пример 4.6. Решить уравнение Бернулли относительно .

.

Полагая , получим

. (4.4)

Уравнение имеет частное решение . Подставляя значение u в уравнение (4.4), перейдем к уравнению

.

Отсюда .