1.2.5. Интегрирование функций, содержащих квадратный трехчлен в знаменателе
Интегралы вида
и 
приводятся к табличным путем выделения полного квадрата в знаменателе дроби.
Пример 1.15.
.
Для вычисления интегралов вида
и 
надо
сначала в числителе дроби выделить
дифференциал трехчлена
,
то есть выражение
.
Пример 1.16.
.
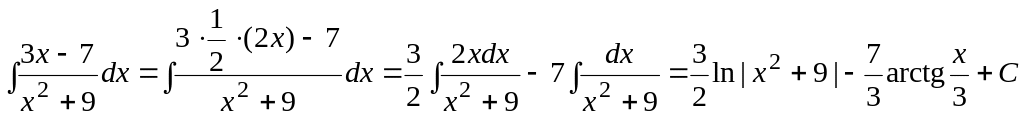1.2.6. Интегрирование рациональных дробей
Рациональной функцией R(x) называется функция, равная отношению двух многочленов:
,
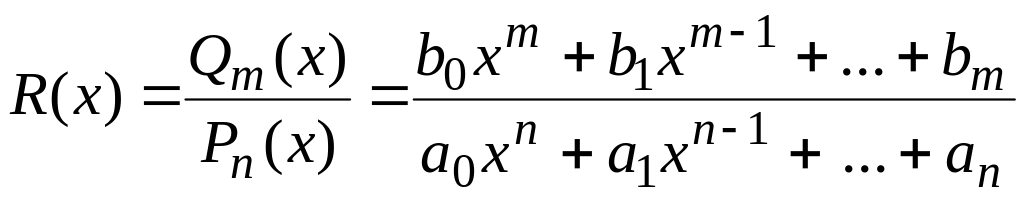где m и n – целые положительные числа;
.
Если m < n, то R(x) называется правильной дробью, если m n, – неправильной дробью.
Всякую неправильную дробь путем деления числителя на знаменатель можно представить в виде суммы некоторого многочлена и правильной дроби:
,
где
,
,
– многочлены,
– правильная
дробь, l < n.
Так как всякий многочлен легко интегрируется, то интегрирование рациональных функций сводится к интегрированию правильных дробей.
Простейшей дробью называется дробь одного из следующих четырех типов:
где A, a, M, N, p, q – постоянные числа;
k 2; k – натуральное, p2 – 4q < 0.
Для интегрирования правильной дроби необходимо:
1) разложить знаменатель дроби на простые линейные и квадратичные множители;
2) представить дробь в виде суммы простейших дробей с неопределенными коэффициентами;
3) найти коэффициенты;
4) проинтегрировать простейшие дроби.
Пример 1.17.
.
Дробь неправильная, поэтому сначала разделим числитель подынтегральной дроби на знаменатель:
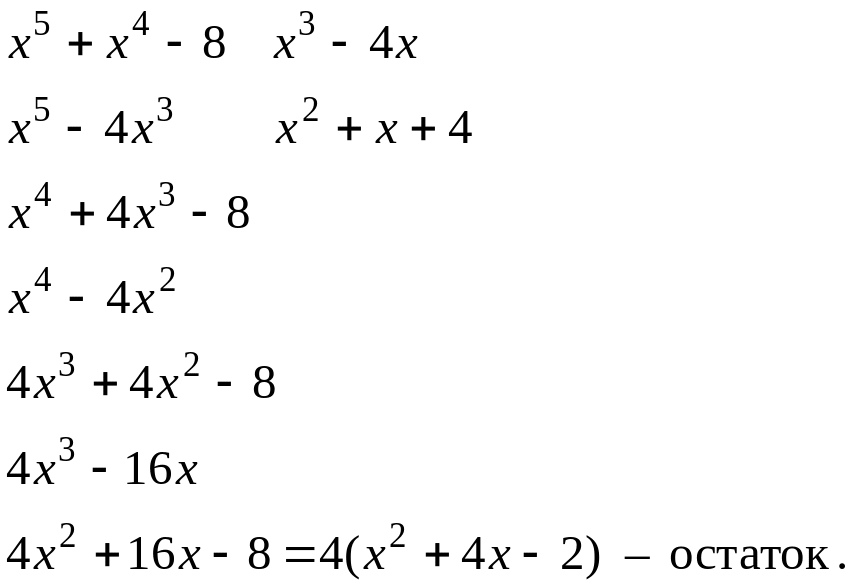
Подынтегральная дробь запишется в виде:
.
Разложим правильную дробь на три простейшие дроби:
.
Приравняв числители, получим тождество:
.
При
:
.
При
:
.
При
:
.
Таким образом,
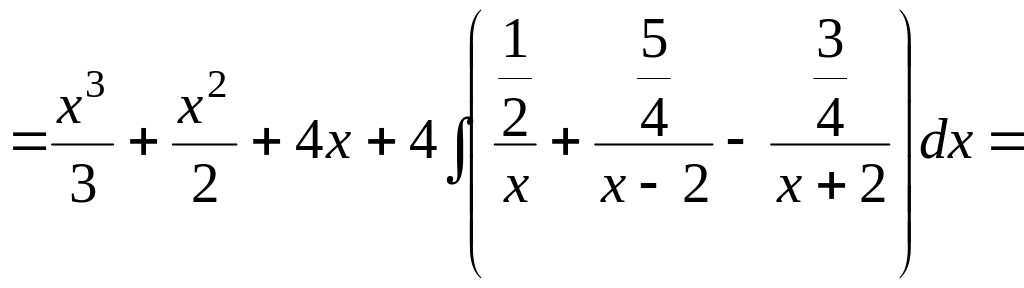
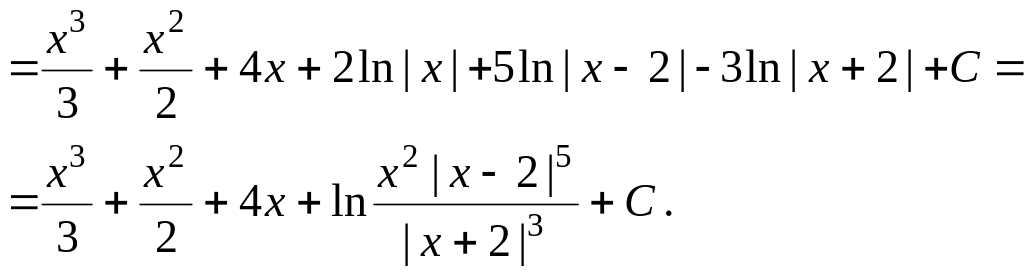
Пример 1.18.
.
В данном примере подынтегральная функция является неправильной дробью. Путем деления числителя на знаменатель выделим целую часть рациональной дроби и правильную рациональную дробь:
.
Правильную
рациональную дробь
представим в виде суммы простейших
дробей с неопределенными коэффициентами:
.
Приведя дроби к общему знаменателю и приравняв числители дробей в левой и правой частях записанного равенства, получим:
.
Приравняв коэффициенты при одинаковых степенях x, имеем:
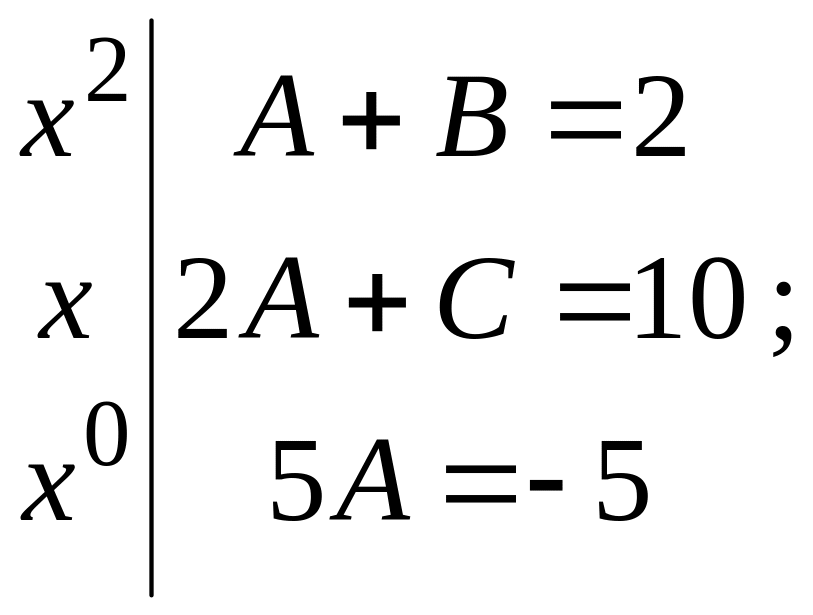
откуда
,
B = 3, C = 12. В итоге получаем
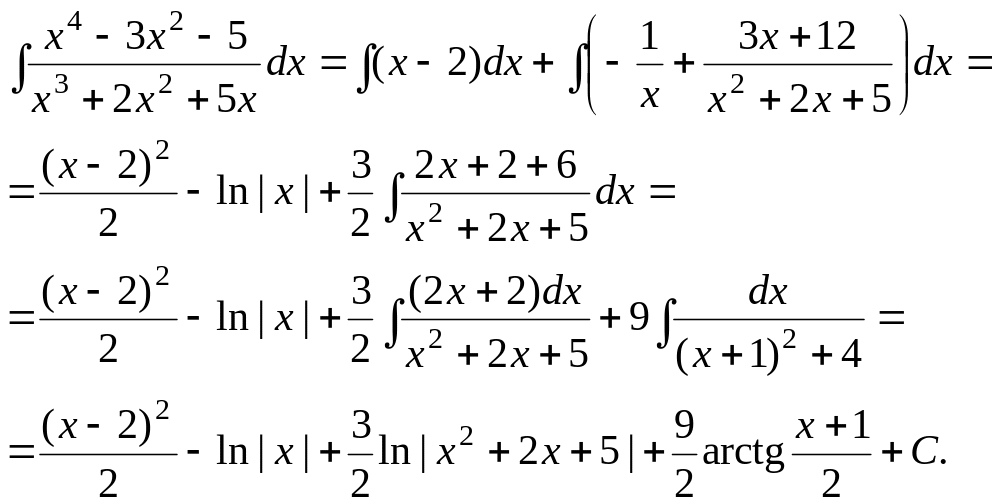
1.2.7. Интегрирование тригонометрических функций
Рассмотрим интеграл вида
,
m, n – целые числа.
1. Если хотя бы одно
из чисел m или n – нечетное и
положительное, то интеграл находится
с помощью подстановок:
или
.
2. Если m и n – четные положительные числа, то применяются формулы понижения степени:
.
Пример 1.19.
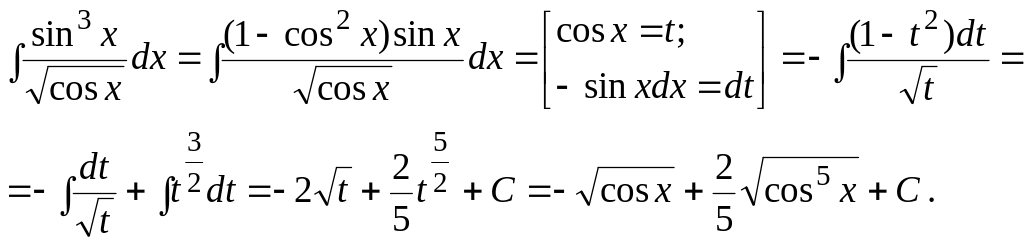
Пример 1.20.
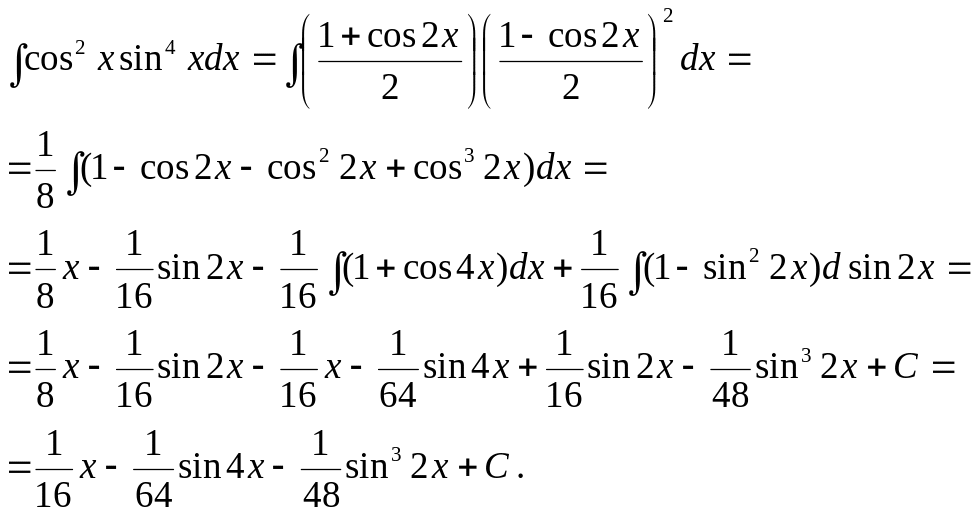
3. Если подынтегральные функции имеют вид
,
где m n, то их преобразуют по формулам:
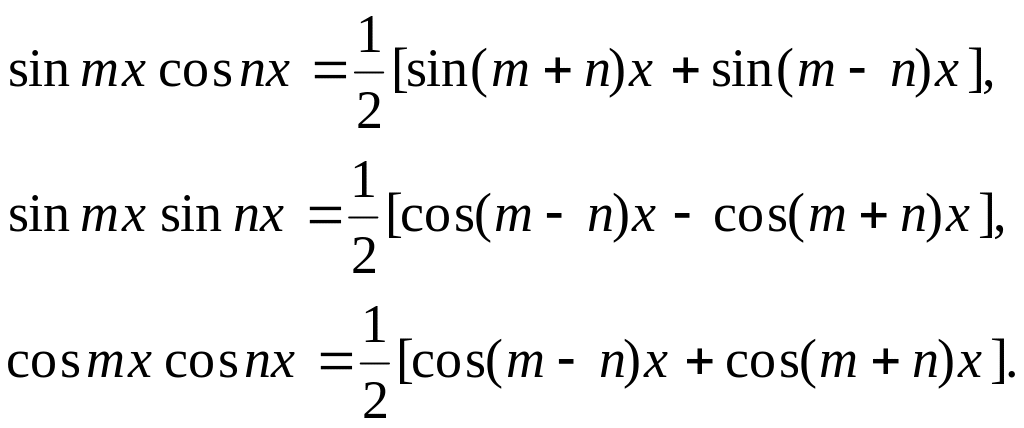
4. Интегралы от
функций, содержащих
где m и n – целые, приводятся к
табличным с учетом формул
.
Пример 1.21.
Здесь
.
5. Интеграл вида
,
где R(u, v) – рациональная
функция от u, v, всегда сводится
к интегралу от рациональной функции
относительно нового аргумента t с
помощью подстановки:
;
тогда
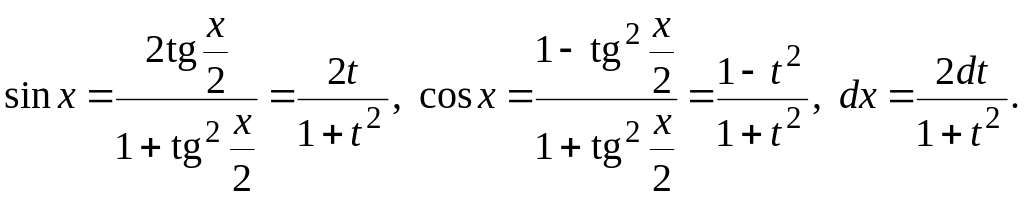
Пример 1.22.
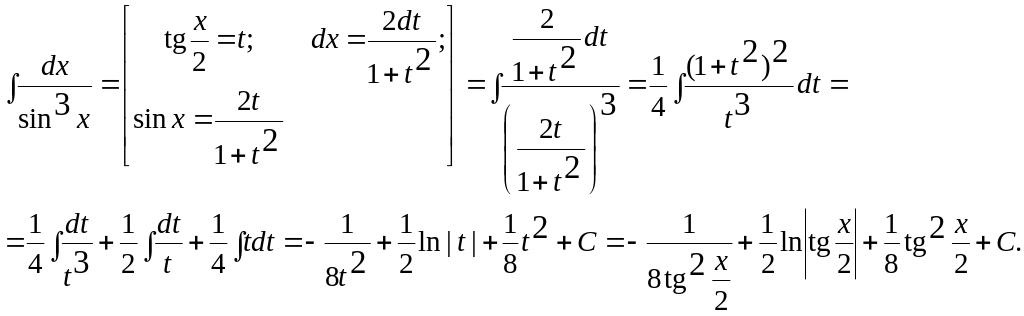
6. Если подынтегральная
функция содержит только функцию tg x
или
(R – четная), то удобно применять
подстановку tg x = t; при этом
.
Пример 1.23.
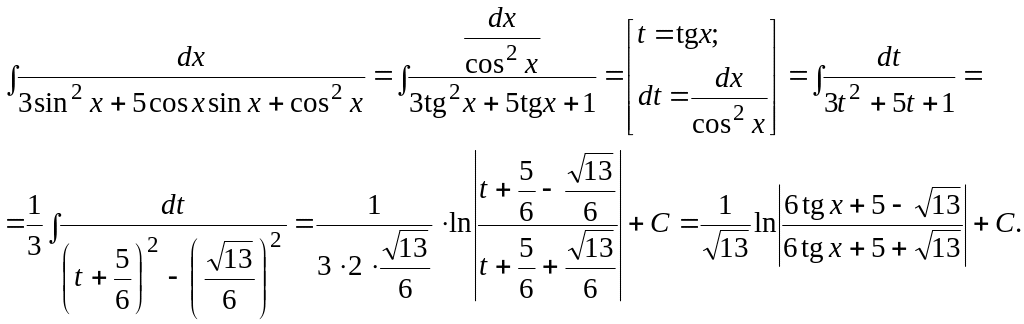
7. Если функция
,
то применяется подстановка cos x =
t. Если
,
то применяется подстановка sin x =
t.
Пример 1.24. 
.
Обозначим cos x = t, sin xdx =
dt; тогда
