3.3.3. Полный дифференциал функции
Полным приращением
функции
в точке
соответствующим приращениям аргументов
,
называется разность
.
Функция u = f(P)
называется дифференцируемой в точке
,
если в некоторой окрестности этой точки
полное приращение функции может быть
представлено в виде
,
где
;
– числа, не зависящие от
.
Полным дифференциалом
du 1-го порядка функции
в точке
называется главная часть полного
приращения этой функции в рассматриваемой
точке, линейная относительно
,
то есть
.
Дифференциалы независимых переменных по определению принимаются равными их приращениям:
.
Для полного дифференциала функции справедлива формула
.
Пример 3.4.
Найти полный дифференциал функции
.
Решение.
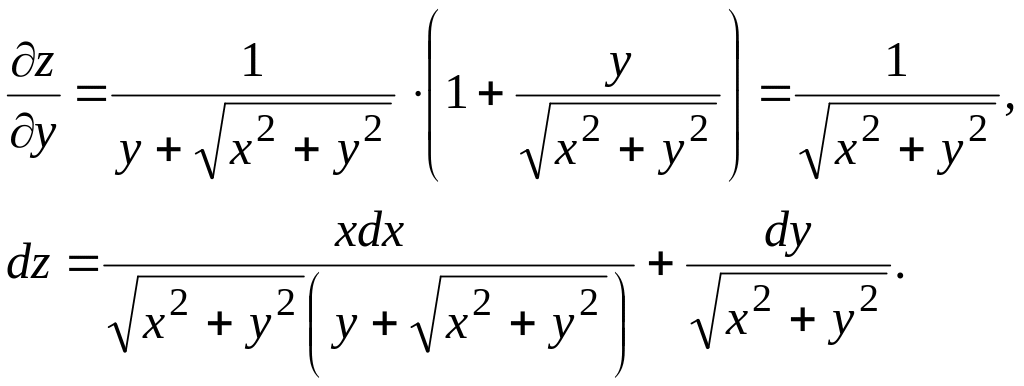
Полный дифференциал
используется для приближенных вычислений
значений функции. Так, например, для
функции двух переменных
,
заменив
,
получим
.
Пример 3.5.
Вычислить приближенно с помощью полного
дифференциала
.
Решение.
Рассмотрим функцию
.
Применив вышеуказанную формулу к этой
функции, получим
или, после соответствующих преобразований,
.
Положим теперь x = 2, y = 1, x = –0,03, y = 0,02. Тогда
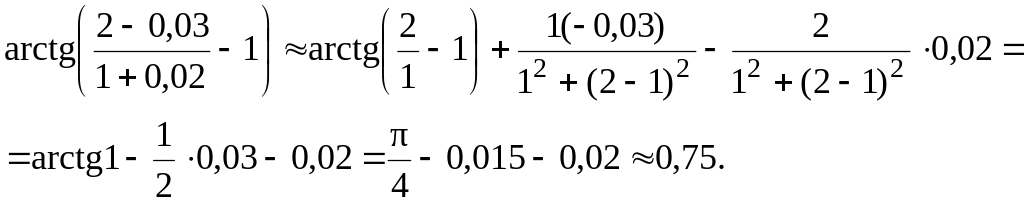
3.3.4. Дифференцирование сложных и неявных функций
Функция z = f(u,v), где u = (x), v = (x), называется сложной функцией переменных x и y. Для нахождения частных производных сложных функций испо-
льзуются следующие формулы:
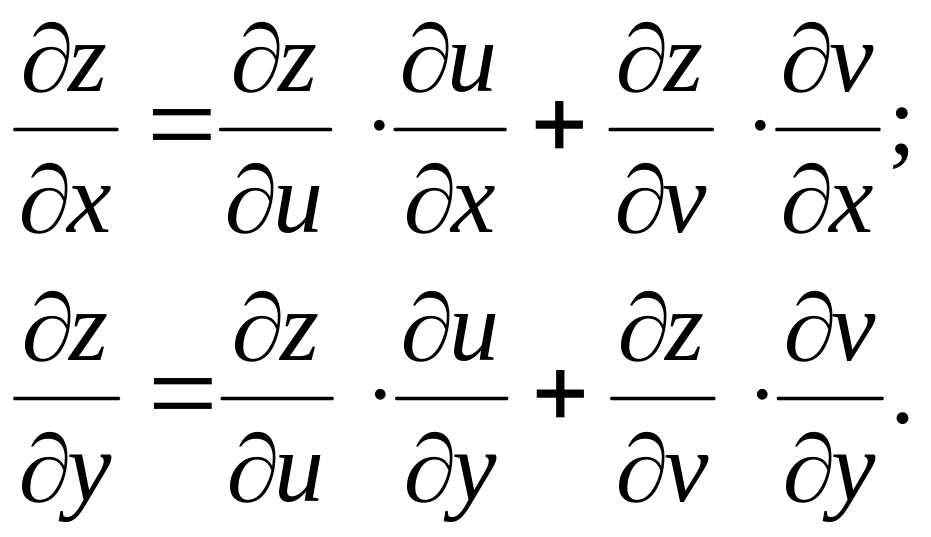
В случае, когда u
= (x), v
= (x), будет:
– функция одной переменной и,
соответственно,
.
Пример
3.6. Найти
частные производные функции
,
где u =
x +
y,
v = x – y.
Решение. По
формуле
имеем:
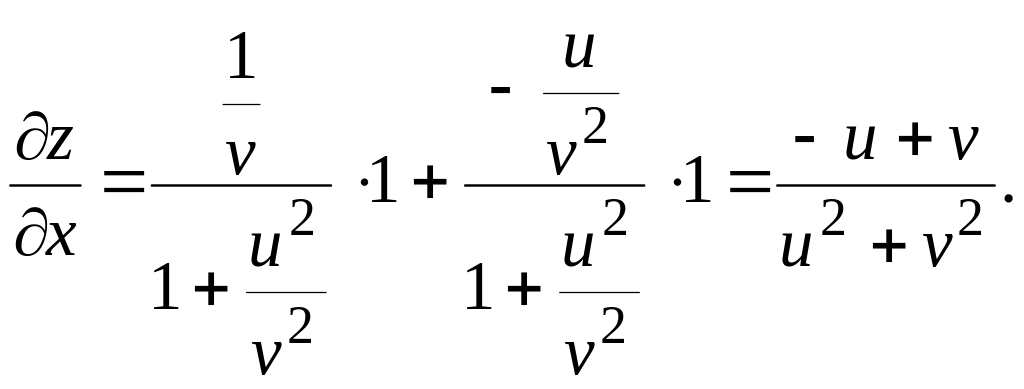
Аналогично
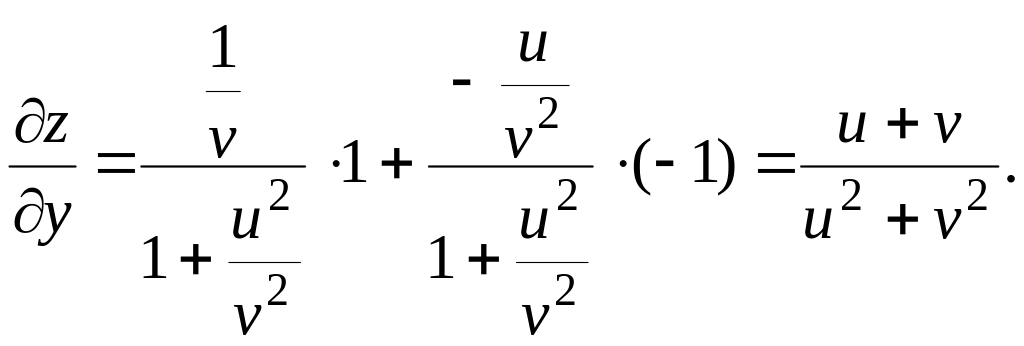
Если уравнение
F(x, y) = 0 задает некоторую
функцию y(x) в неявном виде и
,
то
.
Если уравнение
задает функцию двух переменных
в неявном виде и
,
то справедливы формулы:
Пример 3.7.
Найти частные производные функции z,
заданной неявно уравнением
.
Решение.
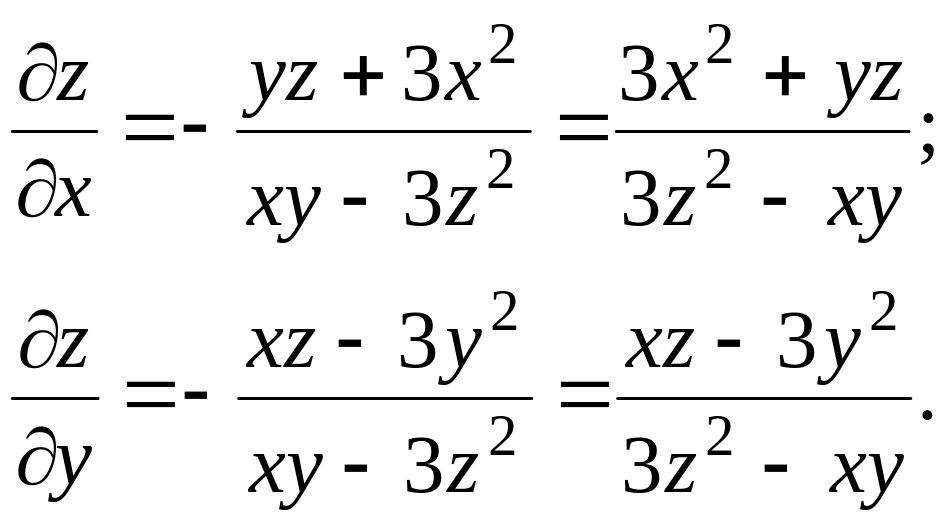
3.4. Касательная плоскость и нормаль к поверхности
Если поверхность
задана уравнением z = f(x, y),
то уравнение касательной плоскости в
точке
к данной поверхности:
,
а каноническое уравнение нормали, проведенной через точку поверхности, таково:
.
В случае, когда уравнение поверхности задано в неявном виде: F(x, y, z) = 0, уравнение касательной плоскости в точке имеет вид
,
а уравнение нормали
.
Пример 3.8.
Найти уравнения касательной плоскости
и нормали к однополостному гиперболоиду
в точке P0(2; –1; 1).
Решение.
Поэтому уравнение
касательной плоскости к данной поверхности
запишется в виде
или
,
а уравнение нормали в виде
или 
.
3.5. Экстремум функции нескольких переменных
Функция
имеет максимум (минимум) в точке
,
если существует такая окрестность точки
P0, для всех точек
которой, отличных от точки P0,
выполняется неравенство
(соответственно
).
Необходимое
условие экстремума. Если дифференцируемая
функция
достигает экстремума в точке P0,
то в этой точке все частные производные
1-го порядка
.
Точки, в которых
все частные производные равны нулю,
называются стационарными точками
функции
.
Достаточные
условия экстремума. В случае функции
двух переменных достаточные условия
экстремума можно сформулировать
следующим образом. Пусть
– стационарная точка функции
,
причем эта функция дважды дифференцируема
в некоторой окрестности точки P0
и все ее вторые частные производные
непрерывны в точке P0. Обозначим
.
Тогда:
1) если D > 0, то в точке функция имеет экстремум, а именно: максимум при A < 0 (C < 0) и минимум при A > 0 (C > 0);
2) если D < 0, то экстремум в точке отсутствует;
3) если D = 0, то требуется дополнительное исследование.
Пример 3.9.
Исследовать на экстремум функцию
.
Решение. Найдем частные производные 1-го порядка и приравняем их нулю.
Получаем систему:
Решая систему,
найдем две стационарные точки
и
.
Найдем частные производные 2-го порядка:
.
Затем
составим дискриминант
для каждой стационарной точки.
Для точки
:
;
;
;
.
Следовательно, экстремума в точке
нет.
Для
точки
:
;
;
;
.
Следовательно, в точке
функция имеет минимум, равный
.