Бесконечно малые и бесконечно большие функции.

Определение 8 (бесконечно малая функция). Функция называется бесконечно малой в точке a или при x a, если

lim_x  af(x) = 0

Пример 10.  f(x) = 1/x, x   f(x) = x2, x  0  f(x) = 1-cos x, x  0

Заметим, что если функция f(x) имеет предел в точке a, равный A, то функция (x) = f(x)-A является бесконечно малой в точке a. То есть, если функция f(x) имеет предел A в точке a, то f(x) = A+, где lim_x a (x) = 0.

Отметим некоторые свойства бесконечно малых функций.

Теорема 4 (свойства бесконечно малых функций).

1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

2. Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая.

3. Произведение конечного числа бесконечно малых является бесконечно малой.

Доказательство. Докажем для примера первое утверждение теоремы для двух бесконечно малых.

Из того, что существует lim_x a(x) = 0, следует, что >0 ₁()>0 такое, что  x: 0<|x-a|<₁ выполняется неравенство |(x)|< /2. Аналогично, из существования предела lim_x a (x) = 0, следует >0 ₂()>0 такое, что  x: 0<|x-a|<₂  выполняется неравенство |(x)|< /2. Тогда  x: 0<|x-a|< = min{₁,₂} выполнятся оба неравенства одновременно, то есть

|(x)+(x)| |(x)|+|(x)|<.

Определение 9 (бесконечно большая функция). Функция называется бесконечно большой при x a или в точке a, если для любого положительного числа  найдется такое положительное (), что для всех x a и удовлетворяющих условию |x-a|< будет выполнено неравенство |f(x)|> .

Аналогично можно дать определение бесконечно большой при x. Приведем его в символической записи:

lim_xf(x) = >0 ()>0  x:|x|> |f(x)|>.

Определение 7.1   Вертикальной асимптотой графика функции   называется вертикальная прямая  , если   или   при каком-либо из условий:  ,  ,  . Заметим, что мы при этом не требуем, чтобы точка   принадлежала области определения функции  , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки:   или  , где  .     

 Определение 7.2   Наклонной асимптотой графика функции   при   называется прямая  , если выполнены два условия:  1) некоторый луч   целиком содержится в  ;  2) расстояние по вертикали между графиком и прямой стремится к 0 при  :

(7.1)

Наклонной асимптотой графика функции   при   называется прямая  , если  1) некоторый луч   целиком содержится в  ;  2) расстояние по вертикали между графиком и прямой стремится к 0 при  :

    

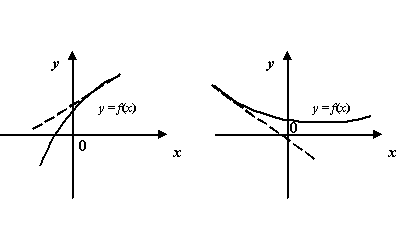
Рис.7.6.Графики функций, имеющие наклонные асимптоты при   и при 

В случае, если наклонная асимптота расположена горизонтально, то есть при  , она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямая   является горизонтальной асимптотой графика   при   или  , если

или

соответственно.

  Определение 7.3   Линия   называется асимптотической линией графика функции   при   (или при  ), если обе эти функции определены на некотором луче   (или луче  ) и разность ординат графиков стремится к 0 при   (или при  , соответственно).     

Если функция   -- линейная, то есть график   -- наклонная прямая, то асимптотическая линия -- это наклонная асимптота. Однако и другие линии бывает естественно рассматривать в качестве асимптотических.

Теорема 7.1   Прямая   служит наклонной асимптотой для графика   при   (или при  ) в том и только том случае, когда

(7.2)

и

(7.3)

(соответственно, есл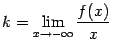и

 и 

Таким образом, для нахождения наклонной (или горизонтальной, если получится  ) асимптоты достаточно найти два указанных предела   и, затем,  . Прямая   будет искомой асимптотой. Если же какой-либо из этих двух пределов не существует, то нет и соответствующей асимптоты.

        Доказательство теоремы.     Докажем теорему в случае  ; доказательство при   проводится совершенно аналогично.

Перепишем условие (7.1), задающее асимптоту, в виде

Так как первый множитель  , то второй множитель, стоящий в квадратных скобках, должен быть бесконечно малым, то есть

Но 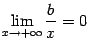  и  , так что

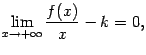
откуда следует равенство (7.2). Теперь число   уже известно.

Подставляя это число в формулу (7.1), находим, что

откуда следует равенство (7.3).      

ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ

Пусть при x→ x₀ с какой-либо стороны функция y = f(x)неограниченно возрастает по абсолютной величине, т.е.   или   или  . Тогда из определения асимптоты следует, что прямая x = x₀является асимптотой. Очевидно и обратное, если прямая x = x₀ является асимптотой, т. о.  .

Т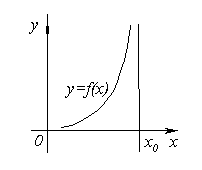 аким образом, вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x→ x₀ – 0 или x → x₀ + 0, x = x₀

Следовательно, для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x₀, при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение x = x₀.

Примеры.

1. Найти вертикальные асимптоты графика функции  .

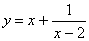Так как  , то прямая x = 2 является вертикальной асимптотой.

2. .

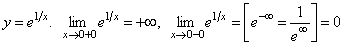Прямая x = 0 – вертикальная асимптота.

НАКЛОННЫЕ АСИМПТОТЫ

Поскольку асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту, то ее уравнение будет y = kx + b. Наша задача найти коэффициенты k и b.

Т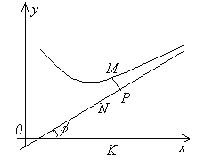 еорема. Прямая y = kx + b служит наклонной асимптотой при x → +∞ для графика функции y = f(x) тогда и только тогда, когда  . Аналогичное утверждение верно и при x → –∞.

Доказательство. Пусть MP – длина отрезка, равного расстоянию от точки M до асимптоты. По условию  . Обозначим через φ угол наклона асимптоты к оси Ox. Тогда из ΔMNP следует, что  . Так как φ постоянный угол (φ ≠ π/2), то  , но

MN = MK – NK = y - y_ас = f(x) - (kx+b).

Следовательно, мы можем записать следующее равенство  .

Так как x → +∞, то должно выполняться равенство  . Но при постоянных k и b   и  . Следовательно,  , т.е.  .

Если число k уже известно, то  , поэтому  .

Для доказательства в случае x → –∞  все рассуждения аналогичны.

Докажем обратное утверждение. Предположим, что существуют пределы, определяющие числа k и b. Тогда несложно заметить, что выполняется равенство  . Действительно

Следовательно, прямая y = kx + b есть асимптота. Теорема полностью доказана.