
- •24) Бесконечно большая последовательность. Доказать теорему о связи бесконечно малой и бесконечно большой последовательностей.
- •31) Бесконечно малая функция. Доказать теорему о функции, её пределе и бесконечно малой функции.
- •52) Доказать теорему о производной обратной функции.
- •45) Производная, её геометрический смысл. Вывести формулы касательной и нормали к графику функции в точке.
- •55) Дать определения максимума и минимума в точке. Доказать необходимое условие экстремума функции в точке (теорему Ферма). Дать определения стационарных и критических точек.
- •56) Доказать теорему Роля и теорему Лагранжа о конечном приращении функции. Рассказать о геометрической интерпретации этих теорем.
- •8) Выпуклость вниз и выпуклость вверх графика функции в точке. Точки перегиба графика функции.
- •57) Доказать достаточные условия максимума и минимума функции в точке.
- •Экстремум функции и необходимое условие экстремума
- •Свойства предела функции.
- •Бесконечно малые и бесконечно большие функции.
- •Определение предела функции
- •Односторонние пределы
8) Выпуклость вниз и выпуклость вверх графика функции в точке. Точки перегиба графика функции.
График имеет выпуклость вверх, если касательная к графику в этой точке находится над графиком. График имеет выпуклость вниз, если касательная в этой точке находится под графиком.
В том случает, если производная в точке равна нулю, а экстремума в этой точке нет, на графике функции будет точка перегиба (точка, в которой касательная к кривой пересекает кривую).
57) Доказать достаточные условия максимума и минимума функции в точке.
Пусть функция y=f(x) непрерывна в точке х0 и имеет производную в некоторой окрестности (х0-, х0+) этой точки, тогда:
Если производная в левой полуплоскости точки х0 положительна, а в правой отрицательна, то х0 – точка максимума.
Если производная в левой полуплоскости точки х0 отрицательна, а в правой положительна, то х0 – точка минимума.

Доказательство теоремы Тейлора для одной вещественной переменной
Пусть

где, как указано в формулировке теоремы Тейлора,
![]()
Достаточно показать, что
![]()
Доказательство основано на повторяющемся применении правила Лопиталя. Заметим, что каждое j = 0,1,…,k−1, f = P. Отсюда каждая следующая производная числителя функции hk стремится к нулю в точке x = a, и то же самое справедливо для знаменателя. Тогда
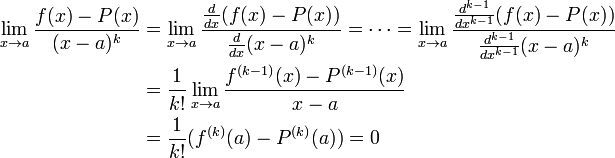
где переход от предпоследнего выражения к последнему следует из определения производной в точке x = a.
Теорема Тейлора даёт приближение к функции, дифференцируемой k раз, вблизи данной точки с помощью многочлена Тейлора k-го порядка. Для аналитических функций многочлен Тейлора в данной точке является конечной последовательностью их неполного ряда Тейлора, который, в свою очередь, полностью определяет функцию в некоторой окрестности точки.
Теорема Тейлора позволяет овладеть приёмами вычислений начального уровня, и она является одним из центральных элементарных инструментов в математическом анализе. При изучении математики она является начальной точкой для изучения асимптотического анализа . Теорема также используется в математической физике. Она также обощает анализ функций нескольких переменных и векторные функции f : R → R для любых измерений n и m.
Правило
Лопиталя представляет
собой метод вычисления пределов, имеющих
неопределенность
типа ![]() или
или ![]() .
Пусть a является
некоторым конечным действительным
числом или равно бесконечности.
.
Пусть a является
некоторым конечным действительным
числом или равно бесконечности.
Если ![]() и
и ![]() ,
то
,
то 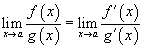 ;
;
Если ![]() и
и ![]() ,
то аналогично
.
,
то аналогично
.
Правило
Лопиталя можно также применять к
неопределенностям типа ![]() .
Первые две неопределенности
.
Первые две неопределенности ![]() можно
свести к типу
или
с
помощью алгебраических преобразований.
А неопределенности
можно
свести к типу
или
с
помощью алгебраических преобразований.
А неопределенности ![]() сводятся
к типу
сводятся
к типу ![]() с
помощью соотношения
с
помощью соотношения
![]()
Правило Лопиталя справедливо также и для односторонних пределов.
1. Докажем
теорему для случая, когда пределы функций
равны нулю (т. н. неопределённость
вида ![]() ).
).
Поскольку
мы рассматриваем функции f и g только
в правой проколотой полуокрестности
точки a,
мы можемнепрерывным
образом их
доопределить в этой точке: пусть f(a)
= g(a)
= 0. Возьмём некоторый x из
рассматриваемой полуокрестности и
применим к отрезку ![]() теорему
Коши.
По этой теореме получим:
теорему
Коши.
По этой теореме получим:
![]() ,
,
но f(a)
= g(a)
= 0, поэтому ![]() .
.
Дальше, записав определение предела отношения производных и обозначив последний через A, из полученного равенства выводим:
![]() для
конечного предела и
для
конечного предела и
![]() для
бесконечного,
для
бесконечного,
что является определением предела отношения функций.
2. Докажем
теорему для неопределённостей вида ![]() .
.
Пусть, для начала, предел отношения производных конечен и равен A. Тогда, при стремлении x к a справа, это отношение можно записать как A + α, где α — O(1). Запишем это условие:
![]() .
.
Зафиксируем t из
отрезка ![]() и
применим теорему
Коши ко
всем x из
отрезка
и
применим теорему
Коши ко
всем x из
отрезка ![]() :
:
![]() ,
что можно привести к следующему виду:
,
что можно привести к следующему виду:
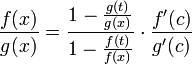 .
.
Для x,
достаточно близких к a,
выражение имеет смысл; предел первого
множителя правой части равен единице
(так как f(t) и g(t) — константы,
а f(x) и g(x) стремятся
к бесконечности). Значит, этот множитель
равен 1 + β, где β — бесконечно
малая функция при стремлении x к a справа.
Выпишем определение этого факта,
используя то же значение ![]() ,
что и в определении для α:
,
что и в определении для α:
![]() .
.
Получили,
что отношение функций представимо в
виде (1 + β)(A +
α), и 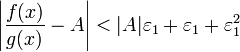 .
По любому данному
можно
найти такое
.
По любому данному
можно
найти такое ![]() ,
чтобы модуль разности отношения функций
и A был
меньше
,
значит, предел отношения функций
действительно равен A.
,
чтобы модуль разности отношения функций
и A был
меньше
,
значит, предел отношения функций
действительно равен A.
Если же предел A бесконечен (допустим, он равен плюс бесконечности), то
![]() .
.
В
определении β будем брать ![]() ;
первый множитель правой части будет
больше 1/2 при x,
достаточно близких к a,
а тогда
;
первый множитель правой части будет
больше 1/2 при x,
достаточно близких к a,
а тогда ![]() .
.
Для других баз доказательства аналогичны приведённым.
Монотонность.
Функция
называется возрастающей на
некотором интервале I ![]() D(f),
если для любых x1, x2
D(f),
если для любых x1, x2 ![]() I,
удовлетворяющих неравенству x1<x2,
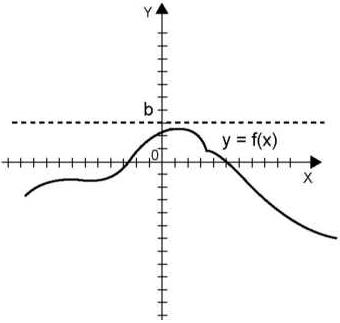
выполняется неравенство f(x1)<f(x2). Пример
возрастающей на интервале функции см.
на рис.5.
I,
удовлетворяющих неравенству x1<x2,
выполняется неравенство f(x1)<f(x2). Пример
возрастающей на интервале функции см.
на рис.5.
Рисунок 5
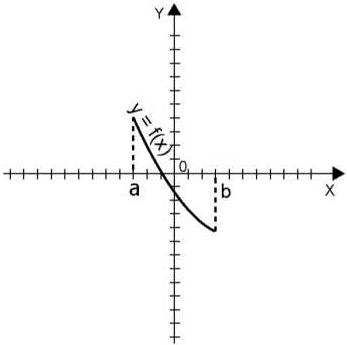
Функция называется убывающей на некотором интервале I D(f), если для любых x1, x2 I, удовлетворяющих неравенству x1<x2, выполняется неравенство f(x1)>f(x2). Пример убывающей на интервале функции см. на рис.6.
Рисунок 6
Если функция является возрастающей или убывающей на интервале I, то она называется монотонной на этом интервале, а I называют интервалом монотонности функции.
Достаточный признак возрастания функции на промежутке: пусть функция y=f(x) определена и непрерывна на интервале I, и в каждой точке этого интервала f'(x)≥0, то функция возрастает на I. Достаточный признак убывания функции на промежутке: пусть функция y=f(x) определена и непрерывна на интервале I, и в каждой точке этого интервала f'(x)≤0, то функция убывает на I.
