
- •7.5. Основные результаты раздела
- •8. Стохастические оптимальные системы
- •8.1. Метод динамического программирования
- •Достаточное условие оптимальности.
- •8.2. Синтез оптимальной системы при полной информации о состоянии
- •8.3. Синтез оптимальных систем управления при неполной информации
- •Наблюдатель Калмана - Бьюси
- •Наблюдатель при цветном шуме объекта
- •Наблюдатель при цветном шуме наблюдения
- •8.4. Стохастическая линейная оптимальная система управления при неполной информации. Принцип разделимости
- •8.5. Основные результаты раздела
- •9. Оптимальные дискретные системы
- •9.1. Синтез оптимальной линейной системы при квадратичном критерии
- •9.2. Стохастическая оптимальная линейная система при полной информации о состоянии
- •9.3. Наблюдатель (фильтр) Калмана
- •9.4. Стохастическая система управления при неполной информации
- •Приложение 1 п1. Функционал и его экстремумы
- •Приложение 2 п2. Матрицы. Дополнительные сведения
- •Характеристическая матрица, характеристические уравнения и собственные значения
9.4. Стохастическая система управления при неполной информации
Пусть объект и наблюдение описываются уравнениями
![]() ;
;
и критерий оптимальности имеет вид
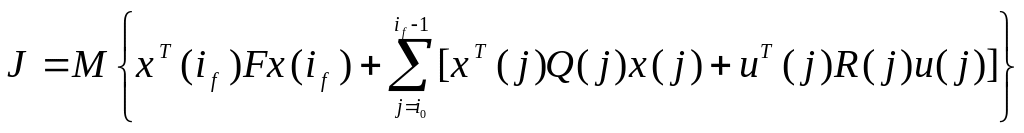 .
.
Шум объекта V0(i)
и шум наблюдения VH(i)
представляют последовательности
независимых гауссовских случайных
величин с нулевыми средними, дисперсионными
матрицами Q0(i)
и R0(i)
соответственно. Матрицы F,
Q(i), R(i), Q0(i)
и R0(i)
симметричны, причем
F0,
Q(i)0,
R(i)>0, Q0(i)0,
R0(i)>0
при i0iij-1.
Начальное состояние x(i0)=x0
является гауссовской случайной величиной
со средним значением
![]() и
дисперсионной матрицей p0
и не зависит от шумов V0(i)
и VH(i).
и
дисперсионной матрицей p0
и не зависит от шумов V0(i)
и VH(i).
Требуется найти такое управление
![]() ,
,
при котором критерий принимает минимальные значения.
Для этой задачи справедлив принцип разделения, поэтому ее решение имеет вид:
![]()
![]()
![]() (9.26)
(9.26)
![]()
![]()
![]()
![]()
![]() (9.27)
(9.27)
Соотношения (9.26)
определяют оптимальное управление с
обратной связью. Они совпадают с
соотношениями (9.13), (9.9), (9.6), определяющими
оптимальный регулятор в случае полной
информации, за исключением того, что в
(9.26) входит оценка
![]() вместо x(i).
вместо x(i).
Оценка получается на выходе фильтра (9.27), совпадающего с фильтром Калмана (9.20) – (9.24). Таким образом, дискретная оптимальная система управления в случае неполной информации, как и аналогичная непрерывная система управления, состоит из оптимального фильтра и оптимального детерминированного регулятора.
Если шумы или значение фазового вектора в начальный момент не являются гауссовскими, то соотношения (9.26), (9.27) определяют линейную оптимальную оценку только в классе линейных систем.
Приложение 1 п1. Функционал и его экстремумы
Функционалом
![]() называется отображение функций заданного
класса М на множестве действительных
чисел, т.е.:
называется отображение функций заданного
класса М на множестве действительных
чисел, т.е.:
![]() ,
,
где
![]() и класс М определяется свойствами
и класс М определяется свойствами
![]() ,
например класс непрерывных функций,
гладких функций и т.п.
,
например класс непрерывных функций,
гладких функций и т.п.
Вполне очевидно,
что для каждого функционала
можно поставить задачу об отыскании
такой функции
![]() (или
некоторого множества функций
(или
некоторого множества функций![]() ),
на которой функционал достигает
экстремального (минимального или
максимального) значения, т.е.
),
на которой функционал достигает
экстремального (минимального или
максимального) значения, т.е.
![]() или
или
![]() ,
,
![]() –
–
для глобального экстремума и
или
,
![]() –
–
для локального экстремума.
Значение первой
вариации функционала
![]() равно линейной относительно вариации
аргумента
равно линейной относительно вариации
аргумента
![]() частью приращения функционала
частью приращения функционала
![]() и является определяющим при отыскании
экстремума
и является определяющим при отыскании
экстремума
![]() .
.
Необходимым условием экстремума функционала является равенство нулю первой вариации функционала
![]() (П1.1)
(П1.1)
а
знак второй вариации
![]() определяет тип экстремума точно так
же, как и второй дифференциал
определяет тип экстремума точно так
же, как и второй дифференциал
![]() для экстремума функции.
для экстремума функции.
Если задан функционал интегрального типа, для которого требуется найти экстремум, т.е.
![]() (П1.2)
(П1.2)
причем концы экстремалей функций, на которых достигается экстремум, фиксированы:
![]() , (П1.3)
, (П1.3)
то условие (П1.1) приводит к уравнению Эйлера
![]() . (П1.4)
. (П1.4)
Отыскание экстремалей состоит в решении уравнения (П1.4) с граничными условиями (П1.3). Это так называемая простейшая задача вариационного исчисления.
Если концы y(a) и y(b) подвижны, то задача поиска экстремума имеет вид
![]() (П
1.5)
(П
1.5)
Её решение отыскивается с использованием уравнения Эйлера совместно с условиями трансверсальности
![]() . (П1.6)
. (П1.6)
Если же не зафиксированы начало х=а и конец х=b, то в этом случае функционал может иметь вид
![]() ,
(П1.5’)
,
(П1.5’)
и для поиска его экстремалей необходимо решать уравнение Эйлера (П1.4) совместно с условиями (П1.6) и дополнительными условиями трансверсальности:
![]() .
(П1.7)
.
(П1.7)
Если в (П1.2), (П1.5) и
(П1.5’) y(x)
есть векторная функция
![]() , то уравнение Эйлера (П1.4) является
системой уравнений для n
координат
, то уравнение Эйлера (П1.4) является
системой уравнений для n
координат
![]() .
.
Точно так же векторными являются краевые условия (П1.3) и условия трансверсальности (П1.6). Условия (П1.7) являются скалярными с участием векторов:
![]() ,
(П1.8)
,
(П1.8)
где Т-символ транспонирования.
В общем n-мерном
случае решение задачи поиска вектор-функции
![]() ,
доставляющей экстремум функционалу
(П1.2), или (П1.5), или (П1.5’), сводится к
следующему:
,
доставляющей экстремум функционалу
(П1.2), или (П1.5), или (П1.5’), сводится к
следующему:
найти общее решение системы n дифференциальных уравнений Эйлера второго порядка (П1.4);
если задача с фиксированными концами, то найти 2n неопределенных констант интегрирования из 2n краевых условий (П1.3);
если задача с подвижными концами, то константы определяются из 2n условий трансверсальности (П1.6);
если не фиксированы концы x=a и/или x=b, то для их определения дополнительно используют условия трансверсальности (П1.7).
В этой схеме решения отсутствие краевого условия по любой i-й координате в x=a или x=b требует использования соответствующего условия трансверсальности и наоборот. Таким образом, в любой комбинации суммарное число краевых условий и условий трансверсальности должно составлять 2n.
Если в решении допускаются негладкие решения, имеющие конечное число угловых точек (точек разрыва производной y(x)), то в таких точках должны выполняться условия Вейерштрасса-Эрдмана:
![]() ,
,
![]() , (П1.9)
, (П1.9)
где с [a,b] является угловой точкой траектории.
Пусть ставится задача об отыскании экстремума функционала
![]() (П1.10)
(П1.10)
при фиксированных условиях на концах (П1.3), но с дополнительными голономными и неголономными связями в виде систем уравнений:
![]()
![]() (П1.11)
(П1.11)
![]()
![]() (П1.12)
(П1.12)
Тогда для решения задачи прежде всего формируется функция Лагранжа
![]() (П1.13)
(П1.13)
где
![]() -
неопределенные коэффициенты или
множители Лагранжа, подлежащие в
дальнейшем определению. Коэффициенты,
стоящие перед уравнениями голономных
связей, являются в общем случае функциями
переменной
-
неопределенные коэффициенты или
множители Лагранжа, подлежащие в
дальнейшем определению. Коэффициенты,
стоящие перед уравнениями голономных
связей, являются в общем случае функциями
переменной
![]() а
а
![]() - константами.
- константами.
Далее решаем вариационную задачу
![]() (П1.14)
(П1.14)
где
![]() Из (П1.13) и (П1.14) следует, что один из
параметров
Из (П1.13) и (П1.14) следует, что один из
параметров
![]() можно выбрать произвольно, т.к. это не
повлияет на результат решения задачи
(П1.14). обычно
фиксируют
можно выбрать произвольно, т.к. это не
повлияет на результат решения задачи
(П1.14). обычно
фиксируют
![]() выбирая
выбирая
![]() в зависимости от вида экстремума.
в зависимости от вида экстремума.
Таким образом,
задача об условном экстремуме функционала
(П1.10) - (П1.12) сводится к задаче о безусловном
экстремуме функционала
![]() (П1.2) – (П1.3).
(П1.2) – (П1.3).
Для её решения необходимо решить уравнение (П1.4), которое в этом случае называется уравнением Эйлера-Лагранжа
![]() , (П1.15)
, (П1.15)
с
учетом уравнений связи (П1.11) и (П1.12), т.к.
вариации по
![]() и
и
![]() приводят (с учетом структуры L
в выражении (П1.3)) именно к ним.
приводят (с учетом структуры L
в выражении (П1.3)) именно к ним.
В многомерном
случае, когда
![]() -
выражение (П1.15) является системой
дифференциальных уравнений с краевыми
векторными условиями.
-
выражение (П1.15) является системой
дифференциальных уравнений с краевыми
векторными условиями.
Если сделать
подвижными концы траектории
![]() и переменными значения a
и b, то можно сформулировать
задачу:
и переменными значения a
и b, то можно сформулировать
задачу:
![]() (П1.16)
(П1.16)
при условиях:
![]() (П1.17)
(П1.17)
![]() (П1.18)
(П1.18)
![]() . (П1.19)
. (П1.19)
тогда,
используя функцию Лагранжа (П1.13) и
функцию
![]() ,
где обычно
,
где обычно
![]() ,
решается задача
,
решается задача
![]() (П1.20)
(П1.20)
которая соответствует задаче (П1.5)–(П1.7). Решение состоит из интегрирования дифференциального уравнения (П1.15) совместно с условиями трансверсальности
![]() (П1.21)
(П1.21)
соответствующими подвижностями границ, и
![]() (П1.22)
(П1.22)
которые соответствуют подвижности концов x = a и x = b.
Если рассматривается
векторная задача размерности n,
и уравнения связи (П1.10) разрешены
относительно
![]() ,т.е.
,т.е.
![]() (П1.23)
(П1.23)
то функция Лагранжа приобретает вид
![]() , (П1.24)
, (П1.24)
и уравнения (П 1.20)-(П 1.22) принимают вид
![]() , (П1.25)
, (П1.25)
![]() (П1.26)
(П1.26)
![]() (П1.27)
(П1.27)
где
![]() , (П1.28)
, (П1.28)
так называемая функция Гамильтона, играющая важную роль в механике и управлении.
