
(1)
Логика – это наука о законах и формах познающего мышления.
Логика изучает мышление, мысл. процессы направлена на обнаружение и обоснование истины, на поиск путей преодоления трудностей в режиме задач в деятельности человека, и в решении задач искусственного интеллекта.
Матлогика – это логика использует мат. методы ми применяется в математике.
Матлогика занимается построением формальных теорий и формальных языков. Предназначена для представления фундаментальных понятий. Например: отношения, функция, аксиома и т.д.
Компоненты формальных теорий:
А) Алфавит
Б) Формулы (вместе – формальный язык)
В)Аксиомы (система)
Г) Правила вывода – по этим правилам из одних верных формул, получаются другие верные формулы.
Опр1: ВЫСКАЗЫВАНИЕ – это утверждение, языковое предложение (не обязательно человека), это может быть выражен не алгоритм. Высказывание может быть либо true либо false.
Новое высказывание, построенное из элементарных высказываний, называется составным высказыванием.
Элементарные высказывания обозначаются пропозициональными переменными: A, B, C, либо с индексами A1, A2…..
Логические связки: ┐, ∩(&), V, →.
Опр1: ┐ ОТРИЦАНИЕ высказывания ┐A – истинно только тогда, когда А ложно. Читается как «не А», «неверно что А».
Опр2: ∩(&) КОНЬЮНКЦИЯ двух высказываний A & B – истинна тогда и только тогда, когда оба высказывания одновременно истинны. (A и B)
Опр3: V ДИЗЮНКЦИЯ двух высказываний A V B – ложна тогда и только тогда, когда оба высказывания одновременно ложны. (A и B)
Опр4: → ИМПЛИКАЦИЯ двух высказываний A → B – ложна тогда и только тогда, когда А истинно, а B ложно. («из А в B», «если A, то B»)
(2) Опр1: ФОРМУЛА (пропозициональная формула) – это составное (в том числе и элементарное высказывание), которое, используя алфавит пропозициональных переменных, строится согласно следующим правилам синтаксиса :
Любая пропозициональная переменная – формула.
Если A и B – то формулами будут являться ┐A, ┐B, A∩B(A&B), AVB, A→B
Формулами будут являться только лишь те высказывания, которые построены по правилам 1 и 2
Опр2: ИНТЕРПРЕТАЦИЯ формулы А – определенное значение истинности формулы А, при подстановки истинностных значений, входящих в нее, пропозициональных переменных.
Пример таблицы истинности для формул:
(3) Опр1: Формула называется выполнимой, если она в некоторой интерпретации принимает значение логической единицы (1)
Опр2: Формула называется опровержимой, если она в данной интерпретации принимает значение логического нуля (0)
Опр3: Формула называется «общезначимой», «тождественно истинной» или «тавтологией» , если она во всех интерпритациях приримает истинное значение (1)
Опр4: Формула называется «невыполнимой»или «противоречивой» , если она во всех интерпретациях ложна (0)
Т1: Пусть А некоторая формула, тогда
1) если А тавтология, то ┐А противоречие, и наоборот.
2) если А противоречие, то ┐А тавтология, и наоборот.
3) если А тавтология, то неверно, что А противоречие, но не наоборот.
4) если А противоречие, то неверно, что А тавтологие, но не наоборот.
Док-во следует из определения
Т2: Если формулы А и (┐А→В) тавтологии, то В тавтология (частный случай правила вывода Modus Ponens)
Док-во методом от противного
а) I(B) = 0
б) I(A) = 1
в) I (А→В) = 1, то условие а противоречит б и в, так как по таблице истинности из 1 → 0 должен быть 0, а у нас 1, противоречие исходному предположению
Наиболее важные тавтологии:
(А→А ) Закон исключенного третьего
А→(В→А), (Аксиома ИВ А1)
Ценное рассуждение (А→В) →((В→С) →(А→С))
(A→(B→C))→((A→B)→(A→С)) (Аксиома ИВ А2)
{ ( A&B)→A; (A&B)→B }
A→(B→(A&B))
A→(A v B)=A→(┐┐A v B) =A→(┐A→B)=B→(A→B)
Аксиома ИВ А3 (┐B→┐A)→((┐B→A)→B)
Закон Пирса(((A→B)→A)→A)
(4) Опр1: Формула B является логическим следованием формулы A, если B - истинно при всех истинных интерпретациях формулы A.
Обозначается A=>B
Опр2: Формулы A и B эквивалентны, если они являются логическим следствием друг друга., иначе говоря, если совпадают их значения истинности во всех интерпретациях
Обозначается AB или A∞B
Основные эквивалентности:
A&B=B&A ; AvB=BvA (коммутативность или перестановка)
A&A=A ; AvA=A (идемпотентность)
(A&B)&C=A&(B&C) ; (AvB)vC= Av(BvC) (ассоциативность)
A&(BvC)=(A&B)v(A&V) ; Av(B&C)= (AvB)&(AvC) (дистрибутивность)
A&(AvB)=A ; Av(A&C) поглощение
┐┐A=A инволютивность
┐(A&B) = ┐A v ┐B ; ┐(AvB)=
┐A&┐B (Привила де’Моргана)
(A&B)v(A&┐B)=A&(Bv┐B)=A&1=A ;(AvB)&(Av┐B)=Av(B&┐B)=Av0=A
(A→B)= ┐AvB
10. (AB)=(A→B)&(B→A)= (┐AvB)&(┐BvA)= ┐A & ┐B v A&B
AvB= ┐┐AvB= ┐A→B
A&B= ┐┐A& ┐┐B =
┐(┐A v ┐B )= ┐(A→B)
Av0=A ; A&0=0
Av1=1 ; A&1=A
A v ┐A=1 (тавтология)
A & ┐A=0 (противоречие)
Т1:
P1 & P2 & …… Pn =>Q
Эта формула является логическим следованием тогда и только тогда, когда эта формула является тавтологией.
Док-во:
Необходимость:
Логическое следование является необходимым условием тавтологии. I(P1 & P2 & …… Pn)=1 (*) – так как эта формула является логическим следованием (по определению) должны выполняться интерпретации:
А)I(Q)=1 (**) ;I(P1 & P2 & …… Pn =>Q)=1
Б) I(P1 & P2 & …… Pn =>Q)=0
При любой интерпретации I(Q)=(1 или 0)
Видно, что эта формула тавтология.
Достаточность:
Наоборот, дана тавтология, доказать логическое следование.
Достаточно приравнять интерпретации
I(P1 & P2 & …… Pn )=1 (*) и I(Q)=1 (**) (согласно определению лог. След.);
I(Q)=1 иначе это не тавтология.
Т2: P1 & P2 & …… Pn =>Q
Эта формула является логическим следованием тогда и только тогда, когда P1 & P2 & …… Pn & ┐Q является противоречием.
Док-во:
Доказывается на основе предыдущей теоремы, с использованием основной эквивалентности A&B= ┐(A→B)
(5) Опр1: Формальные теории - вначале разрабатывались для формализации логики и теории доказательства. Основа матлогики – ФТ.
Состав произвольной формальной теории Г:
Множество А – символов алфавита (как конечное, так и бесконечное)
F – множество слов в алфавите А. Эти слова иначе называются формулами. F может быть бесконечным.
Замечание1: Множества F и A обозначают ЯЗЫК – семантику.
Множество B принадлежащее F – образует аксиомы (система аксиом)
R – множество отношений r. R принадлежит R, и принадлежит Fn+1. R – называют правилами вывода.
Замечание2: Множество F строится индуктивным способом
Замечание3: Множество B может быть как конечным так и бесконечным, если оно бесконечно, то оно строится с помощью конечного множества схем аксиом и правил порождения конкретных аксиом.
Замечание4: Множество правил вывода R как правило конечно.
Опр2: Формула G называется выводимой формулой из формул F1 … Fn, по правилу вывода r, если существует такое правило вывода r, что (F1 … Fn, G) принадлежит r:
![]()
где G – заключение, F – послание.
Опр3: Выводом формулы G из формул F1…Fn формальной теории Г, называется последовательность формул, E1,E2…Ek, где Ek=G, а любая Ei(i<k) может быть:
Ei=Fj , j=1,n
Ei – какая либо из аксиом
Ei – выводима непосредственно из Ej1,Ej2…Ejm, где jm<i
Символическое обозначение вывода: F1,F2…Fn├ Г G
Опр3:
Вывод формулы G
только лишь из аксиом называется Теоремой
![]()
Посылки в выводе называются гипотезами.
Дополнение к выводу лишних гипотез сохраняет выводимость.
Если
верен вывод
![]() ,
то верен и
,
то верен и
![]()
Опр4: Интерпретацией ФТ в область интерпретаций М, будем называть отображение множества F во мн-во M:
I:F→M Если соответствующее высказывание является истинным, то говорят что формула выполняется в данной интерпретации
Опр4: I – называется моделью ФТ, если все ее теоремы выходят в интерпретацию I.
(6) Опр9: Формула G называется логическим следствием множества формул Г если формула G выполняется в любой модели Г
Опр: ФТ Г – называется семантически непротиворечивой, если ни одна ее теория не является противоречием.
Опр: ФТ Г – называется формально не противоречивой если в ней не являются одновременно выводимыми формулы F и ┐F
МЕТАТЕОРЕМА I : Модель для ФТ Г существует тогда и только тогда, когда Г семантически не противоречива.
МЕТАТЕОРЕМА II : ФТ Г формально не противоречиво тогда и только тогда, когда она семантически не противоречива
Опр: ФТ Г называется полной (или адекватной) если любому истинному высказыванию относительно М соответствует теорема в ФТ Г
Опр:Если для множества М существует формальная, полная и непротиворечивая теория, то М – называется аксиоматизируемым множеством (формализуемым множеством)
Опр:Система аксиом (аксиоматизация) формально не противоречивой теории Г называется независимой, если никакая из аксиом не выводима из остальных аксиом Г по правилу этой теории Г.
Опр: ФТ Г называется разрешимой, если существует алгоритм, который для любой формулы этой теории способен определить является ли эта формула теоремой этой теории.
Теория будет называться полу разрешимой, если существует алгоритм, который для любой формулы теории
(7) Опр1: Исчисление высказываний – это Формальная Теория L, в которой:
Алфавит, кроме лог. связок, (┐, →, (, )):
a,b,c,d,e…..
A,B,C,D,E…
Формулы:
Любые переменные - это формулы
Если A и B – формулы, то ┐A, ┐B, A→B – формулы
Аксиомы А1,А2,А3:
А1: A→(B→A) – аксиома упрощения
А2: (A→(B→C))→((A→B)→(A→C)) – аксиома самодистрибутивности
А3: ((┐B→┐A)→((┐B→A)→B))
![]()
MP:= “Modus Ponens” (лат. «Правило вывода»)
Опр2: Если в формуле С:=А(X1…Xn) вместо переменных х1...хn осуществить групповую подстановку {Bi||Xi}i=1, то таким образом полученная формула называется частным случаем формулы A(X1…Xn), а само выражение называется УНИФИКАТОРОМ.
Опр3: Если формула C, является частным случаем формул A и C:=D(x1…xn), то формула C называется совместным частным случаем формул A и B, а сами формулы A и B называются унификаторами. Формула A набор ??? называется общим унификатором, возможен он не один.
Наименьший унификатор называется наиболее общим унификатором.
Опр4: Набор формул B1…Bn называется частным случаем набор A1…An, если для любая формула Bi является частным случаем формулы Аi на одном и том же наборе подстановок.
Опр5: Набор C1…Cn является совместным частным случаем наборов A1..An и B1…Bn, если любая формула Ci является частным случаем формул Ai и Bi.
(8) Другие аксиоматизации:
Гильберта - Аккерчона
Россера
Клини
Никода
Лучасевича
Енсена
Новикова
Аксиомы Клини:
A1: (A→(B→A))
A2: ((A→(B→C))→((A→B)→(A→C))
A3: (A→(AvB))
A4: (B→(AvB))
A5: ((A&B)→A)
A6: ((A&B)→B)
A7: ((A→B)→((A→ ┐B)→ ┐A))
A8: ((A→C)→((B→C)→((AvB)→C)))
A9: (A→(B→(A&B)))
A10: ┐┐A=A
Т1:
![]()
Используя аксиому А1 и подстановку B:= A→A т.е. получим A→((A→A)→A)
Используя аксиому A2 и подстановку {B:=A→A; C:=A} получим (A→((A→A)→A) → (A→(A→A)) → (A→A)
Применяем MP
Используя аксиому А1 и подстановку B:=A получим A→(A→A)
Применяем MP
Т2:
![]()
A – гипотеза
A├A→(B→A)
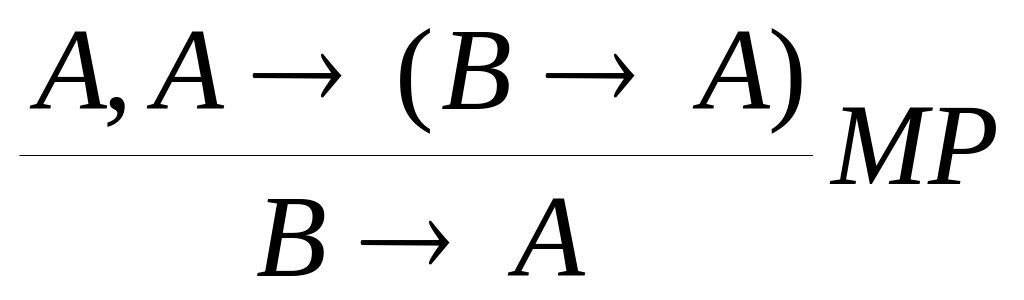
Смысл
теорем в получении произвольного правила
вывода из правила MP,
в качестве доказанной выводимости,
которая называется введение имплекации,
им. Условное обозначение:![]()
(9)
Т1 Теорема
дедукции: Формула B
– выводима из формулы A
(доказуема) тогда и только тогда, когда
выводима формула A→B.
Если
![]() ,
то
,
то![]() и наоборот.
и наоборот.
I Доказательство прямой теоремы.
Необходимо доказать:
Если
![]() →последовательность
формул, имеем вывод → имеем последовательность
выводимых формул.
→последовательность
формул, имеем вывод → имеем последовательность
выводимых формул.
E1……En=B
Здесь возможны следующие частные случаи:
E1-Аксиома
E1 принадлежит Г
E1=A
Доказательство
метода математической дедукции, в
соответствии с которым необходимо
проверить, доказать вывод,
![]() ,
а так-же опирается на индуктивные
предположени
,
а так-же опирается на индуктивные
предположени
![]() ,
,
на
базе которого 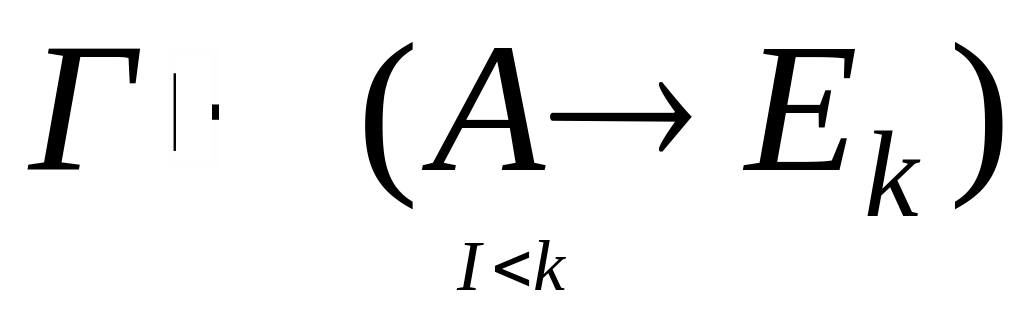
Док.
Вывода
![]()
E1 – аксиома
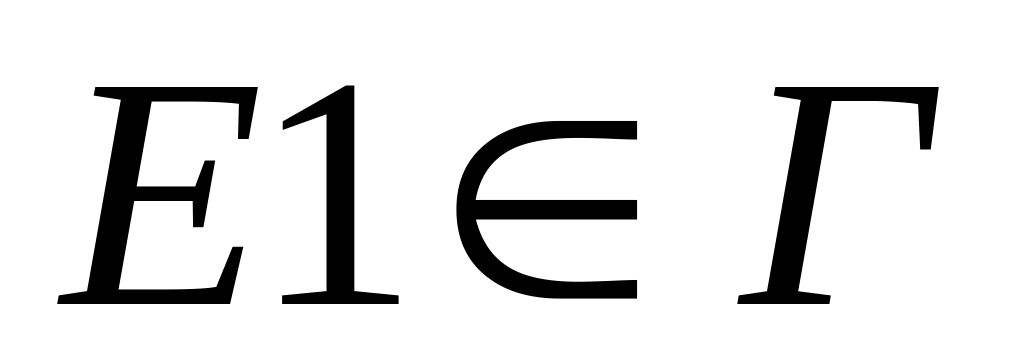
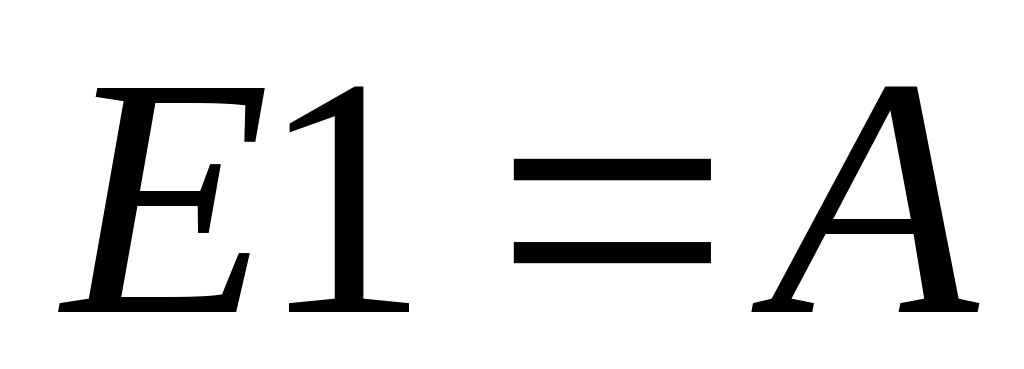
E1,E1→(A→E1),A→E1
Доказательство 1-2 выглядит одинаково с помощью теоремы 2
1) ,
![]() ,
,![]()
(подстановка {E1||A,A||B})
2) Аналогично первому
3) Для третьего случая используем теорему 1
![]()
Добавление лишних гипотез не меняет свойств выводимости
![]()
Доказаны все случаи 1, 2, 3 для стартового этапа метода математической индукции!
Верны индуктивные предположения:
![]() ,
где i,
j<k
,
где i,
j<k
E1,E2…Ei-1,Ei…Ek…En=B
Ek из последовательности вывода E1…E2 , т.е. из формул Ei и Ej, согласно основному правилу MP
Ej=Ei→Ek
![]() ,
этот особый случай обозначим за (4’), а
первые 3 случая абсолютно аналогично,
как и для начального этапа.
,
этот особый случай обозначим за (4’), а
первые 3 случая абсолютно аналогично,
как и для начального этапа.
Первые 3’ пункта доказываются по аналогии с пунктами, доказанными ранее, а для доказательства четвертого пункта используем аксиому А2(самодвойственность) с подстановкой {Ej||B,Ek||C}.
A2: (A→(B→C))→((A→B)→(A→C))
После подстановки получаем:
![]()
Еще раз применим MP:
![]()
Получим вывод в конечной форме которого:
Г,А├А→Ek
По методу математической индукции исходя из пунктов 1 и 2 справедлив вывод для любого К, даже k=n:
Г,А├А→En=B
ПРЯМАЯ ТЕОРЕМА ДОКАЗАНА!
II Обратная теорема
Дано: Г├А→B, необходимо доказать Г,A├B
A – гипотеза
A→B выводима по условию теоремы
3)
(10)
Следствие
1: если
![]() ,
то
,
то
![]() и обратно
и обратно
Доказательство:
Г:=0
Следствие
2: правило «транзитивности»
![]()
Доказательство:
A→B гипотеза.
B→C гипотеза
А гипотеза
A→B, B→C, A├С по теореме дедукции получаем
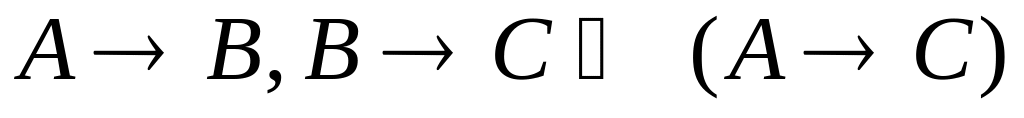
![]() –
–
Следовательно, вывод верен.
Теорема Дедукции
Этот вывод эквивалентен новому производному правилу – правилу транзитивности
Следствие
3: правило «сечения»
![]()
Доказательство:
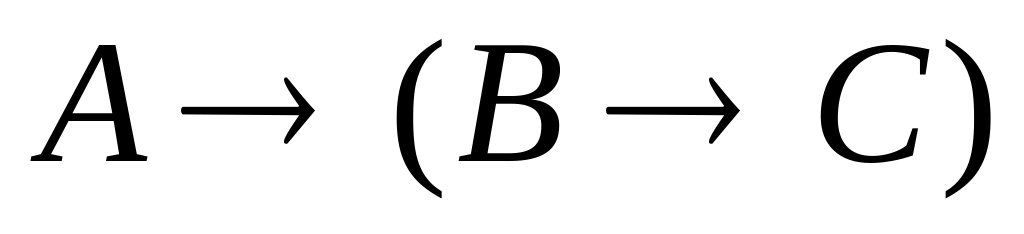 -
гипотеза.
-
гипотеза.B – гипотеза
A – гипотеза
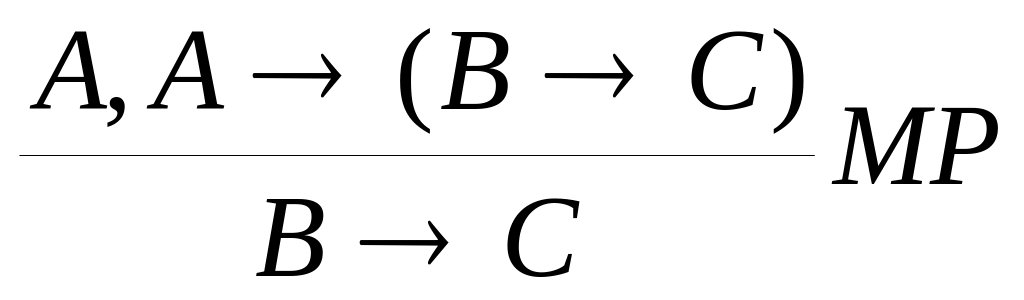

Вывод 1, 2, 3, 4, 5 верен иначе говоря:

Правило сечения!
(11) Теорема: В теории L выводимы следующие формулы
ТеоремаА:

ТеоремаБ:
Т еорема
В:
еорема
В:
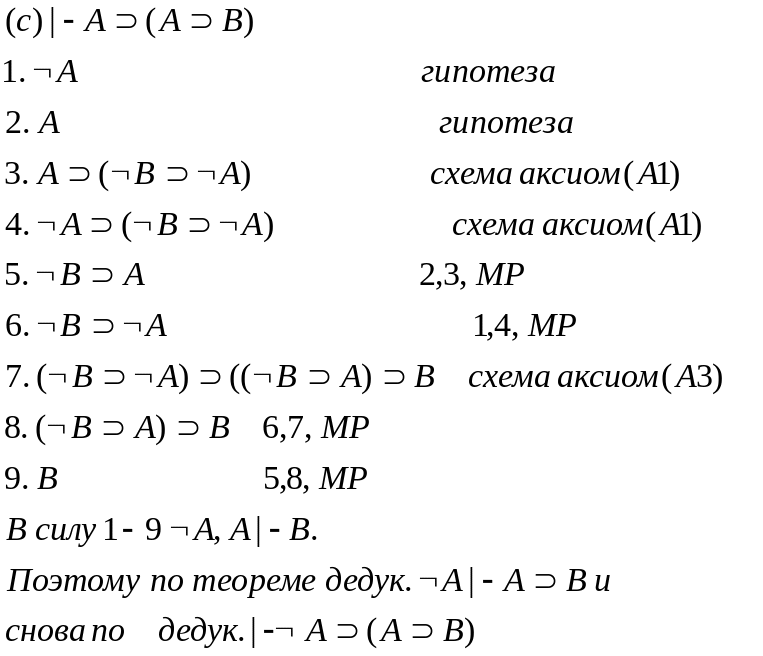
(12)
Множество
теорем ИВ: доказательство леммы
![]()
Используя способ по индукции по структуре формулы
(1) А = аi, A` = a`
a`├ a` по дедукции ├ a`→ a` будет верна, так как она совпадает с теоремой или ├ А`→ А`
Теорема 1 то есть по обратной дедукции верно А`├ А` или a`├ a` добавление лишних гипотез не влияет на истинность теоремы
(2) А = ┐B т.е. по индукц. Предположению лемма верна для формулы В
![]()
Если I(B) = И тогда В`= B, I(A) = Л
А`= ┐A = ┐B на основании теоремы о добавлении двойного отрицания
├ В→┐┐В, по МР
![]()
то
![]()
I(B) = Л, В`= ┐B, I(A) = И, А`=А=┐B=B`
т.е. А`=B`
![]()
(3) А=В→С т.е. по инд. Предположению верны выводы
![]()
![]()
а)I(В) = Л тогда при любом значении I(С) имеем что I(A) = И т.е. А`=А=В→С
┐А→(А→В) {B//A, C//B}, ┐B→(B→C)=A по МР
![]()
Данный а) эквивалентен подпунктам I(С) = И и I(С) = Л
б) I(В) = И, I(С) = И тогда I(A) = И, т.е. А`=А=В→С, С`=C, B`=B
![]()
![]()
А1 {C//A} C→(B→C)=A=A`
![]()
в) I(В) = И, I(С) = Л, I(А) = Л, т.е.
![]()
С`=┐C, B`=B
![]()
![]()
Используя теорему подстановки вместо {B//A, C//B}
![]()
![]()
![]()
(13) Множество теорем ИВ (А - тавтология)
В
теоремах теории L
выводимыми формулами являются общ.
формулами (тавтологией) и только они
![]()
1)
Обратная Дано А – тавтология, Доказать
![]()
Доказательств:
используя лемму
![]()
Аi` = {ai, I(ai) = И; ┐ai, I(ai) = Л}
![]()
Используя теорему дедукции
![]()
Используя теорему
и МР два раза получим
![]()
Аналогичным
образом проделываем вышеописанную
процедуру n-1
раз и в результате получим
![]()
Прямая теорема
![]() Дано
Дано
Доказать что А – тавтология
А1,А2,А3 – аксиомы – тавтологии ()
Правило вывода из тавтологий А1-А3 МР сохраняет свойство тавтологичности, поэтому результирующие формулы в теоремах также будут тавтологиями.
Приведённая метатеорема указывает на свойство полноты теории L(ИВ).
Следствие из метатеоремы
Теория L формально непротиворечива
Доказательство:
Для
формально непротиворечивой теории не
могут быть верны теоремы
![]() и
и![]() (одновременно),
так как на основании метатеоремы мы
заключили что выводимой формулой
является лишь тавтология, но
непротиворечивая, поэтому не могут быть
выводимы одновременно тавтология и
противоречие, значит теория формально
непротиворечива.
(одновременно),
так как на основании метатеоремы мы
заключили что выводимой формулой
является лишь тавтология, но
непротиворечивая, поэтому не могут быть
выводимы одновременно тавтология и
противоречие, значит теория формально
непротиворечива.
(14) Опр1: Исчисление предикатов (ИП) 1-ого порядка – это формальная теория К, в которой определены следующие компоненты:
Алфавит:
Логические связки (основные) ┐, →, (дополнительные) &, v
Служебные скобки (,).
Кванторы
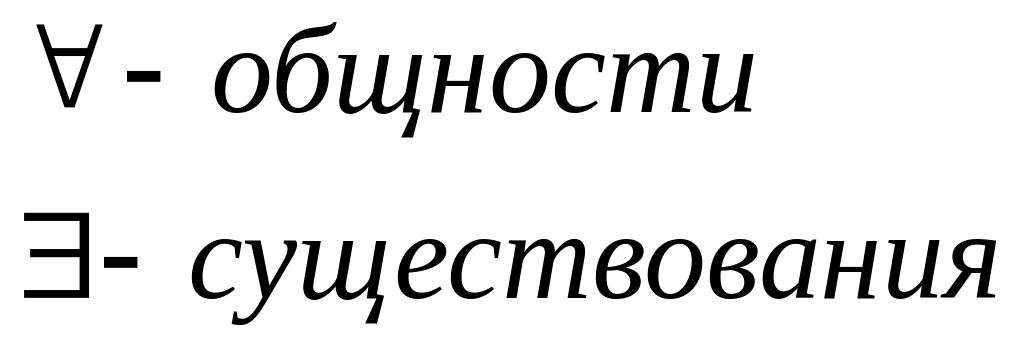
-
Предметные константы a, b, c
Предметные переменные x, y, z : x1, y1, z1 …
Предметные предикаты P, Q, R
Предметные функторы f, p, g
X2+X2=R2 – функтор
<, ≤, >, ≥, =, ≠ - предикаты
Опр2: Вхождение переменных в атомарные формулы A и B называется свободным, если они не связаны квантором. Это вхождение будет также свободным и в формулах ┐А, ┐B, A→B, и наоборот связанным если их объединяют кванторы.
Опр3: Формулы А и ┐А, где А – атомарная формула, называются контрарными литералами.
Опр4: Терм t(…x…) для переменной x, в формуле A(…x…t(x)…), называется свободным, если никакое свободное вхождение переменной x в формуле A не лежит в области действий по переменной y входящей в терм t.
Опр5: ИП – не содержащее предметных констант, функторов, предикатов, собственных (не логических) аксиом предметной области – называется ЧИСТЫМ (узким) ИП, в противном случае ПРИКЛАДНЫМ.
(15) Интерпретация ИП
В I(Приклад ИП) с областью интерпретации (носитель М) – это набор функций которые сопоставляют:
а) в каждой предметной константе а элемент носителя I(a) принадлежит М
б) каждому функтору f сопоставляет операцию I(f) на носителе
в) Каждому
n-местному предикату Р
сопоставляется отношения I(P),
I(P)
![]() М
М
Свойство
1) Пусть х=(х1,х2,...,хn)
S=(s1,s2,…,sn)
T=(t1,t2,…,tn)
![]() f(t1,t2,…,tn)
f(t1,t2,…,tn)
S из носителя M:
![]() S*:{t}
→ M
S*:{t}
→ M
a) S*(a) = I(a)
б) S*(xi)=Si
S*(f(t1,t2,…,tn))=I(f)(S*(t1),S*(t2),…,S*(tn))
S*(P) = I(P)= (S*(t1),S*(t2),…,S*(tn))
Всегда определ. истинностное значение для любой формулы для любого атом. формулы носителя
3) Если истинностное значение S*(P)=И, то формула P выполнима на наборе S
4) Формула ┐А выполнима на наборе S титтк формула А невыполнима на этом наборе S
5) A→B(Формула) выполнима на наборе S титтк формула А невыполнима на S или формула В выполнима на S
6) Формула
![]() выполнима
на S титтк А выполнима на
любом наборе S` отличающемся
от набора S возможно только
лишь i-ым компонентом
выполнима
на S титтк А выполнима на
любом наборе S` отличающемся
от набора S возможно только
лишь i-ым компонентом
7) S` выполнима на S титтк A выполнима на каком либо наборе S` отличным от S возможно только лишь i-ым компонентом
8) Формула называется истин. На любой интерпретации I если она выполнима на любом наборе S из носителя M
9) Формула ложна в данной интерпретации I если она не выполнима на любом наборе S из носителя М
10) Интерпретация называется моделью множества Г если все формулы из Г истинны в данной интерпретации
11) Любая замкнутая формула истинна или ложна в данной интерпретации
Открытая(незамкнутая) формула А(x,y,z…) титтк её замыкание истинно в данной интерпретации
Вывод собствен. нелогич. аксиомы прикладной теории пишутся в открытой форме
(16) Опр1: Формула ИП общезначима (тавтология) если она истинна в любой интерпретации
Т11:
Формула
![]() ,
где терм t
свободен для переменной x
формулы A,
является тавтологией.
,
где терм t
свободен для переменной x
формулы A,
является тавтологией.
Т12:
Формула
![]() ,
где терм t
свободен для переменной x
формулы A,
является тавтологией.
,
где терм t
свободен для переменной x
формулы A,
является тавтологией.
Т1:Любая теорема ЧИП 1ого порядка в качестве выводимой формулы содержит общезначимую формулу
Т2: Любая общезначимая формула является выводимой формулой ПИП 1-ого порядка.
Свойство формальной непротиворечивости для ЧИП также выполняется
(17) Опр1: Формула B выполнимая на любом наборе в любой интерпретации, на которой выполнима формула A, называется логическим следствием форм. A.
Опр2: Формулы A и B логически эквивалентны AB или A=B, если если они являются логическим следствием друг друга.
Следствия эквивалентности:
1)
![]()
![]()
2)
![]()
![]()
3)
![]()
![]()
4)![]()
![]()
5)
![]()
![]()
6)
![]()
![]()
7)
![]()
![]()
8)
![]()
![]()
9) Для любой формулы A существует логически эквивалентная ей формула A’ в предваренной форме.
(18) Опр1: Теория равенства ε – это ПИП в котором кроме ЧИП дополнительно введены:
Собственный 2-х местный предикат «=» (x=y)
Собственные аксиомы:
E1:
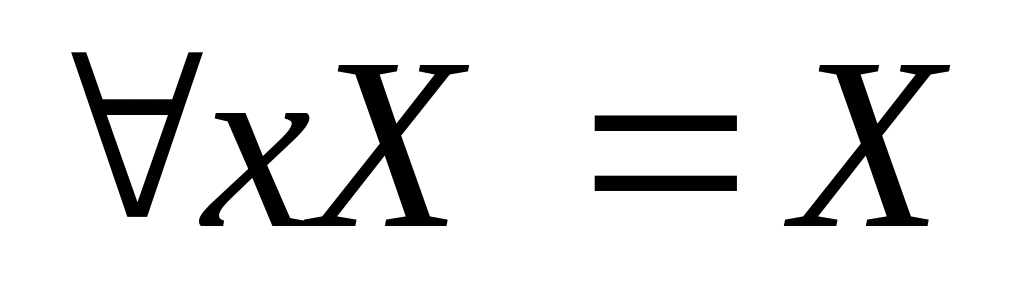
E2:
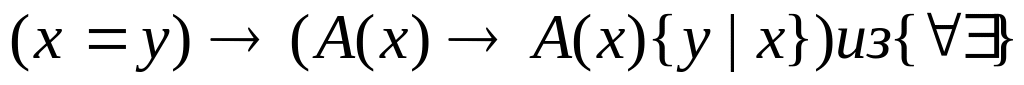
Т 1, 2, 3:
1)
![]() ,
для любого терма (t)
,
для любого терма (t)
(частный случай эквивалентности. Рефлексивность)
2)![]() -симметричность
-симметричность
3)
![]() -
транзитивность
-
транзитивность
Доказательство:
1)
Из
P1
и E1
=>
![]() =>
{x=x|
|A(x)}
=>t=t
=>
{x=x|
|A(x)}
=>t=t
2)
E2:{x=x|| A(x)}: (x=y)→((x=x)→(y=x))
![]()
2разадедукция назад:![]()
E1 или теорема первая:
![]()
Применяем дедукцию вперед и получаем результат:
![]()
E2:{x=z || A(x), y || x, x || y, x=z || A(x)}
(y=x)→((y=z)→(x=z)) – тавтология
![]() Дедукция
назад
Дедукция
назад
![]() по
второй теореме:
по
второй теореме:
![]() Дедукция
вперед и готов результат:
Дедукция
вперед и готов результат:
![]() Предикат
равенства (отношение равенства) на
основе теорем 1, 2, 3 – обладает свойствами
рефлексивности, симметричности,
транзитивности, значит отношение
равенства является отношением
эквивалентности, но оно является его
частным случаем, и является более сильным
отношением эквивалентности чем другие.
Элементы понимаются как абсолютно
совпадающие.
Предикат
равенства (отношение равенства) на
основе теорем 1, 2, 3 – обладает свойствами
рефлексивности, симметричности,
транзитивности, значит отношение
равенства является отношением
эквивалентности, но оно является его
частным случаем, и является более сильным
отношением эквивалентности чем другие.
Элементы понимаются как абсолютно
совпадающие.
(19) Опр1: Формальная арифметика – это ПИП в котором имеются:
предметные константы – 0
Двуместные функторы +,*
Одноместные функторы P,” ’ ”
Двуместный предикат «=»
Собственные (нелогические) Аксиомы:
A1:
![]()
A2: (t1’=t2’)→(t1=t2)
A3: ┐(t’=0)
A4: (t1=t2)→((t1=t3)→(t2=t3))
A5: (t1=t2)→(t1’=t2’)
A6: t+0=t
A7: t1+t2’=(t1+t2)’
A8: t*0=0
A9: t1*t2’=t1*t2+t1
Чтобы из этой формальной арифметики A получить обычную арифметику, надо одноместный функтор «’» интерпретировать как взятие следующего за текущим элементом t.
(20) Опр1: Группа G – это ПИП с равенством (теория равенств учтена) в которой имеется:
Предметная константа = «0»
Двуместный функтор «+»
Собственные (не логические) аксиомы:
G1:
![]() - ассоциативность
- ассоциативность
G2:
![]()
G3:
![]()
Замечание: В теорию G входит теория равенства со всеми аксиомами, и все следствия из этой теории.
G4:
![]()
Замечание: Если выполняется Аксиома G4, то такая группа называется Абелевой.
Опр2: Абелева группа называется группой конечного порядка n, если выполняется аксиома G5:
G5:
![]()
Опр3: Абелева группа называется полной, если выполняется G6
G6:
![]()
Опр4: Абелева группа называется периодической, если выполняется G7:
G7:
![]() Число k
– должно существовать
Число k
– должно существовать
Метатеорема 1: Во всякой достаточно богатой теории 1-ого порядка существует такая истинная формула f, что ни F и ни ┐F не являются выводами в этой теории.
Метатеорема 2: Во всякой достаточно богатой теории 1-ого порядка формула F, утверждающая непротиворечивость этой теории, не является выводимой в ней.
Интерпретация - пояснение – теорем Геделя не утверждает, что арифметика противоречива, а утверждает, что непротиворечивость собственными формулами теория установить не может.
(21) Постановка задачи:
Алгоритм
АДТ в общем случае для любой теории Г,
для любой формулы S
в ней, не существует, т.е. алгоритм АДТ
должен отвечать «Да», если вывод
![]() справедлив, и «нет» если такой вывод
неверен.
справедлив, и «нет» если такой вывод
неверен.
В частности для теории L (ИВ), и для ПИП 1-ого порядка с одноместным предикатом алгоритмы АДТ известны:
А) (ИВ) – метод таблиц истинности (но не является методом автоматического поиска верных выводов)
Б) Для ПИП – таким методом может служить например метода «резолюций»
Этот метод MR выдает для ПИП 1-ого порядка ответ «Да», если вывод верен и выдает «нет» или зацикливается, если вывод неверен.
Доказательство от противного:
Т1:
Если вывод
![]() -
противоречие, то верен вывод
-
противоречие, то верен вывод
![]()
Доказательство:
1)
![]() по теореме Дедукции =>
по теореме Дедукции =>
![]() -
тавтология
-
тавтология
![]()
![]() -
Обратная Дедукция и получаем:
-
Обратная Дедукция и получаем:
![]()
(22)Опр1:Предложение – бескванторная дизъюнкция литералов (переменных).
Любая формула ИП преобразуется во множество предикат с помощью следующих операции:
Элиминация импликации

Протаскивание отрицаний:
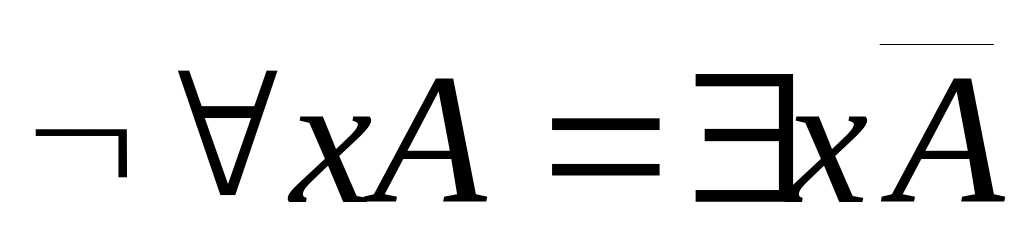
Разделение связанных переменных:
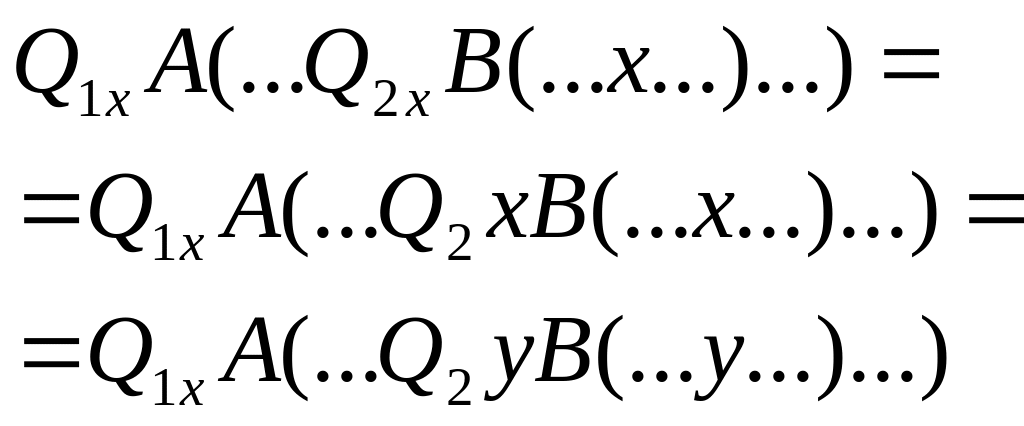
Приведение к предваренной форме (изнутри вытаскиваются все кванторы):
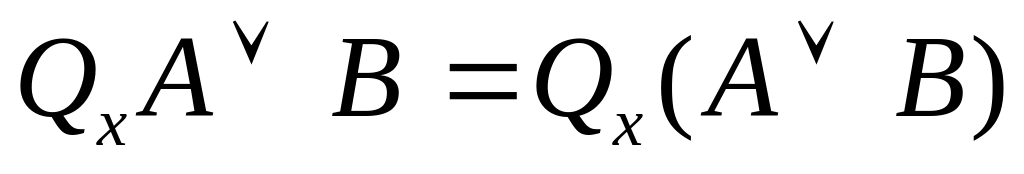
Элиминация квантора :

Элиминация квантора :
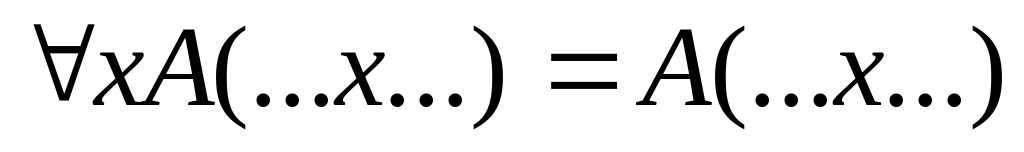
Приведение формы к КНФ:
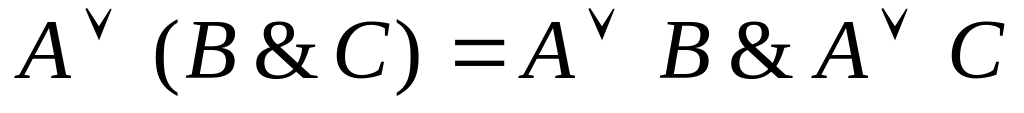
Элиминация конъюнкции (распад на отдельные предложения): A&B , A,B
В результате применения таких операций из 1-8 (в частном случае могут быть применены все 8 операций, и может быть не 1 раз), любая формула преобразуется во множество предложений.
Т1: Если Г – множество предложений полученных из формулы S, то S – является противоречием тогда и только тогда, когда множество Г – невыполнимо, т.е. Г не имеет модели.
Доказательство:
Для доказательства необходимо сначала доказать все 8 операций в отдельности, ранее доказанными теоремами и отдельные операции из 8-и операций имеют тривиальные доказательства, кроме сколемизации квантора существования (элиминации)
Положим,
что наша формула F
=S![]() есть
противоречие.
есть
противоречие.
Множество
Г=F![]() - в формуле А вместо i-ой переменной стоит
- в формуле А вместо i-ой переменной стоит
![]()
Пользуясь методом от противного, считаем, что множество Г, не является противоречием, тогда:
![]()
I(F’)=1
При
этом
![]()
Нан
аборе
![]() I(F)=I(F’)=1
I(F)=I(F’)=1
Получим противоречие, т.к. формула F по условию является противоречием, т.е. множество формул Г является не выполнимым.
(23) Пусть C1 и C2 – произвольные предложения ИВ, за счет произвольности предположим C1’ и C2’:
C1=C1’vP C2=C2’v ┐P
P и ┐P – контральные литералы.
Правило вывода привила резолюции выглядит так:

где C1 и C2 – резольвируемы (родительские предложения), а C1’ и C2’ – резольвенты (дочерние предложения)
Частными случаями этого правила являются:
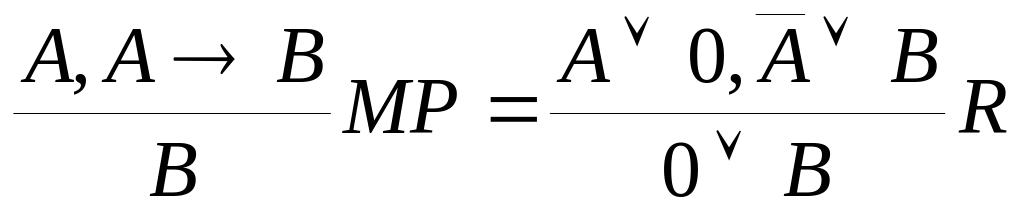
Правило транзитивности:
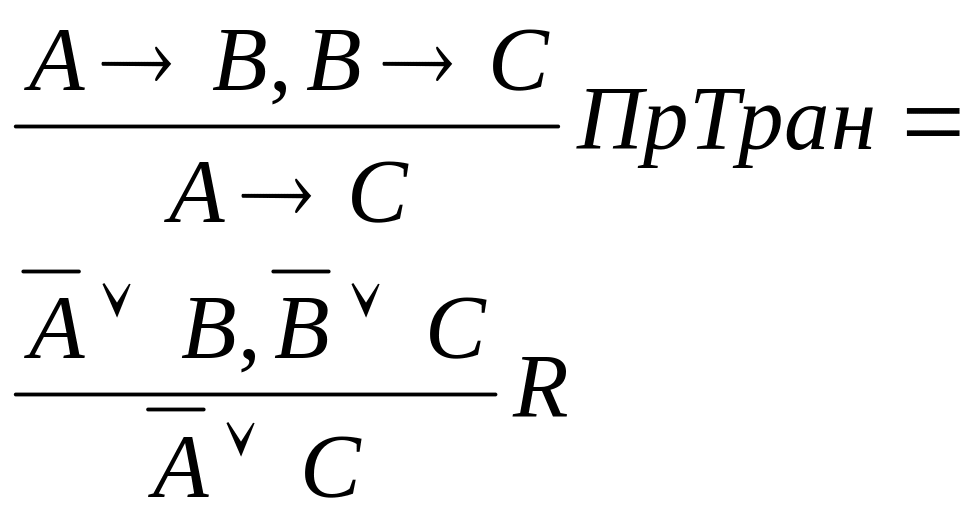
Правило слияния:
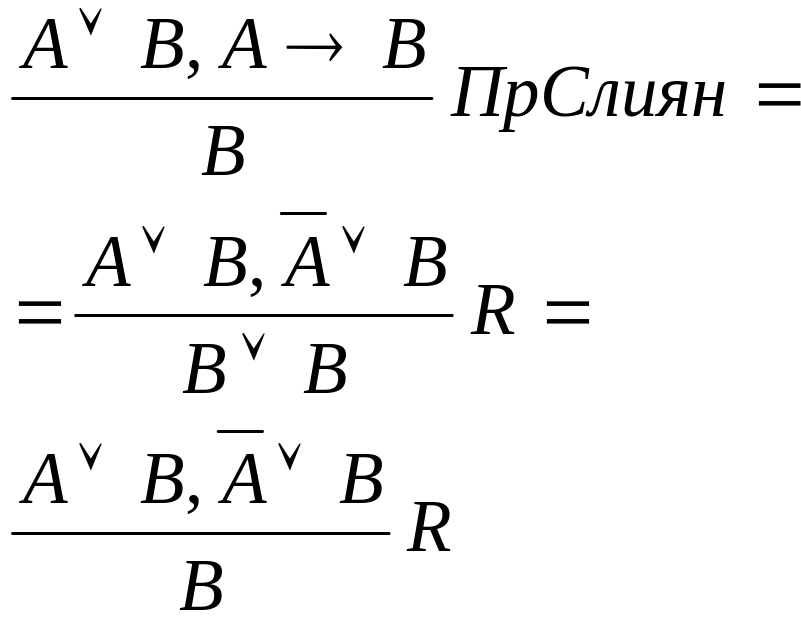
Т1: Правило резолюции логично, т.е. резольвента является логическим следствием резольвируюемых предложений.
I(C1)=1 I(C2)=1
C1=C1’vP
I(P)=0 & C1’≠(0) → I(C1’)=1 I(C1’vC2’)=1
C2=C2’vP
I(P)=1 & C2’≠(0) → I(C2’)=1
I(C2’vC1’)=1
(24)
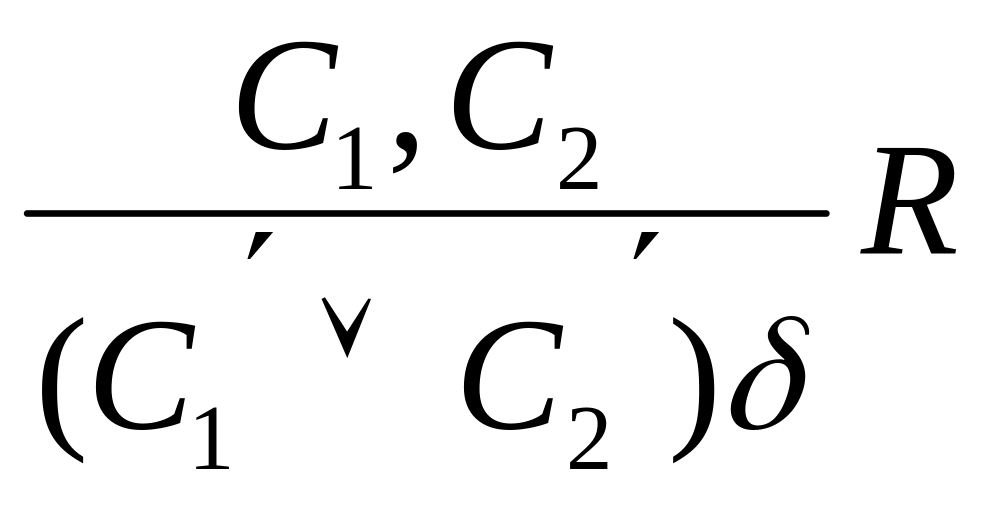
C1, C2 – резольвируемые предложения ИП, которые представлены:
C1=С1’vP1
C2=C2’v ┐P2
P1 и ┐P2 – контральные литералы.
Унифицируемы
общим унификатором
![]()
(P1 и P2) =P
(25) Суть алгоритма:
Нужно
доказать вывод
![]()
Алгоритм:
Каждой из формул множества Г, и формула ┐S (от противного), сводятся во множество предложений С
В полученном совокупном множестве C отыскиваются резольвируемые предложения C1 и C2, к которым применяются правило, к которым применяются правило резолюции, а его результат (резольвента) расширяет множество предложений С.
Продолжать выполнение пунктов 1-2 до тех пор, пока не ьулеи получена пустая резольвента. (C1’vC2’)δ=0, т.е. C1 и C2 образуют противоречие P1&┐P2 и согласно теореме * множество C не имеет модели.
По
методу доказательства от противного
это означает, что S
является выводимой и справедлив вывод
![]()
В этом алгоритме возможны 3 случая:
Среди текущего множества C не находится резольвирующих предложений, т.е. вывод
 неверен.
неверен.В результате очередного шага, получена нулевая резольвента (пустое множество), т.е.
 - верен.
- верен.Процесс пополнения резольвентами множества C не дает пустых резольвент, сколько бы мы этих шагов не производили т.е. алгоритм зацикливается, поэтому он полуразрешим.
(26) Понятие алгоритма и неформальной вычислимости: определения и основные особенности алгоритма. Теория алгоритмов нами рассматривается с фундаментальных позиций. Изучение конкретных алгоритмов их квалиф. Вопросы так же важен ,но в данном аспекте останется вне рамках рассмотрения.
Фундаментальные вопросы:
1)![]() что
для любой разрешимой задачи алгоритм
решения мог бы быть сгенерированным из
этих двух наборов
что
для любой разрешимой задачи алгоритм
решения мог бы быть сгенерированным из
этих двух наборов
2)как распознавать разрешимые и не разрешимые проблемы?
3)что такое вычислимость? эффект вычислимости?
4)что мы должны вкладывать в понятие алгоритм? И тд.
Основные хар-ки и особенности алгоритма:
1)св-во определённости(алг разбивает задачу на более простые шаги)
2)для алг.всегда определены входные данные
3)определен вид представления выходных данных(может быть даже изображение или сигнал)
4)детерминированность-при завершении любого шага всегда определены дальнейшие действия.
![]() конкретные
извесные задачи для которых на уровне
теорем док-но.,что для них не сущ.
Алгоритмов решения.
конкретные
извесные задачи для которых на уровне
теорем док-но.,что для них не сущ.
Алгоритмов решения.
ЗАМ.в
реальных задачах все участвующие объекты
можно кадировать целыми числами.ф-лыопределены
на мн-ве натуральных чисел с нулем.Сами
фун-ции так же принимают значение з
этого мн-ва![]()
![]() n-местное
n-местное
![]()
![]()
ОПР.если
область определения
![]() допускает
значек включения ???????
допускает
значек включения ???????
Т.е. может совпадать с ,то такие фун-ции наз-ют ВСЮДУ ОПРЕДЕЛЁННЫМИ.иначе (если строгое включение)ЧАСТИЧНОопред.
ОПР.фун-ция
ЭФФЕКТИВНО_ВЫЧИСЛЯЕМАЯ,если
![]() алгоритм
вычисляющий её и для алг. Должны
выполнятся условия
алгоритм
вычисляющий её и для алг. Должны
выполнятся условия
![]() в
области опред-ния
в
области опред-ния
2)если
![]() алгоритм
должен зациклится.
алгоритм
должен зациклится.
ЗАМЕЧ.понятие эфеективн-ти вычислимости шире чем понимание алгоритма сводящегося в вычислением на ЭВМ или каких либо устройствах.
(27)Подход Геделя-Клини к формализации понятия алгоритма: Частично-рекурсивные функции (ЧРФ): операторы суперпозиции, примитивной рекурсии, минимизации для построения ЧРФ.Идея Г.Т.получить вче вычислимые ф-ции из существенно ограниченного базиса с помощью простейших алгоритм.средств
А)![]() нулевая
фун-ция
нулевая
фун-ция![]() фун-ция
следования
фун-ция
следования![]() фун-ция
проэкции о от1доN
фун-ция
проэкции о от1доN
Б)1)Оператор
суперпозиции![]()
![]()
![]() и
и
![]()
2)Оператор примитивной рекурсии
Строится(n+1
фун-ция
![]() из
двух фу-ций n-местной
из
двух фу-ций n-местной
![]() и
(n+2)
месной
и
(n+2)
месной
![]() =
=![]() -это
равенство определяется оператор(2)
-это
равенство определяется оператор(2)
(1)
![]()
![]() Вторая
ф-ла реализует св-во рекурсии.Первая
нужна для вычисления стартового
обеспечения условия.ЗАМ.Ф-ция
может
быть рекурсивной по всем предыдущим
переменным.
Вторая
ф-ла реализует св-во рекурсии.Первая
нужна для вычисления стартового
обеспечения условия.ЗАМ.Ф-ция
может
быть рекурсивной по всем предыдущим
переменным.
ПРИМЕР
f(x)-рекурсивная
фун-ция (n+1)местная
т.к. n=0,
h-const=a,![]()
(1): f(0)=a
(2):
f(y+1)=
![]()
1ой и 2ой операторы из всюдуопределённых фук-ций могут получать всюду опред-ные фун-ции.т.е.операторы порождают всюдуопред-ные.Но это не значит что они порождают всё полное прост-во всюдуопред-ных фун-ций т.е. порождают замкнутый класс всюдуопред-ных фун-ций
ЗАМ.Недостающее множество всюду опред-нфх фун-ций порождается сл.оператором.
3)Оператор минимизации
Частичные фун-ции
![]()
![]() которые
опред-ся сл образом :
которые
опред-ся сл образом :
А)область определения
![]()
![]() ,
,![]()
![]()
Б)
![]() равна
наим.знач.для кот выполнено условие
равна
наим.знач.для кот выполнено условие
![]() =
=![]()
ЗАМ.чобы
построить полной пространство частич
опред фун-ций с помощью опрета-ра
минимизации необходимо брать более
широкое мн-во одноместных фун-ций f
,но не каждая фун-ция
![]() может
обращаться в ноль ,при каком-то значении
n+1
аргумент фун-ции h
может не СУщ-ать минимал значения y
.
может
обращаться в ноль ,при каком-то значении
n+1
аргумент фун-ции h
может не СУщ-ать минимал значения y
.
Из всего сказанного следует,что хотя в общем всё мн-во ф-ций ,определённых с помощтю оператора минимизиции, названо нами мн-вом частич опред-ных ф-ций,но часть из них может быть и всюдуопред-ыми,поэтому будем считать что мн-во всюдуопред. Ф-ций включено виде подмножества в полной мн-во всех частич.опред.ф-ций. Т.е. всюду опред.ф-ция –это часный предельный случай ля частично опред.ф-ций.Все три оператора позволяют строить полное-мн-во част.опред.ф-ций включая и все всюдуопред.ф-ции.
ЗАМ.Если мы не оговариваем конкретно с помощью каких операторов построена конкретная ф-ций,то в общем мы предпологаем,что исп опер.прим.рек.Поэтому общее название частич.опред.ф-ций=ЧАСТИЧНО_РЕКУРСИВНЫЕ Ф_ЦИИ.Если же конкретная ф-ция явл-ся всюдуопред-ной,то её будем наз-вать ОБЩАЯ рек-ная ф-ций.Если же ф-ций построена без помощи опре.минимизации,то назовем её ПРИМИТИВНО рекурсивной.
Идея Г-К состоит в том что все вычисляемый фун-ции явл-ся частично рекурс.,как и подходы других авторов с аналогичным тезисом(ток назв ф-ций другие)до сих пор нет строгого док-ва , но и не опровергнуто,а практически подтверждается.СУЩ-ют критерии кот-ый позваляют установить св-во ЧАСТИЧНОЙ рекурсив-ти сразу для общирных классов.ВЫВОД:сущ-ют обще рекурсивные ф-ции которые не могут быть постороенны без применения третьего оператора.
28.Примеры рекурсивности (примитивно-рекурсивных и общерекурсивных функций)
1, сложение двух чисел
SUM:
( X,Y
)![]()
![]() всюду
определённая функция
всюду
определённая функция
1)SUM(X,0)=x
- pr![]() проекция
проекция
![]()
2)SUM(X,Y+1)=(X+Y)+1=S(SUM(X,Y)) ф-ция следования
1)и5)образуют оператор ПРИМЕТИВНОЙ рекурсии,а т.к. всюдуопределена,то она ОБЩЕРЕКУРСИВНА
2,Ф-ция перемножения
Prod: (x,y)=x*y
![]() всюдуопределена
всюдуопределена
1)prod(x.0)=0 нулевая ф-ция
2)prod(x,y+1)=x*y+x=SUM(prod(y.x),x)
1)и2)-ПРИМЕТИВНОрекурсивная![]() ОБЩЕРЕКУРСИВНАЯ
ОБЩЕРЕКУРСИВНАЯ
3,Усечённое вычитание единицы
![]()
![]()
1)![]()
![]() ф-ция
проэкции т.е. ОБЩЕРЕКУРСИВНАЯ
ф-ция
проэкции т.е. ОБЩЕРЕКУРСИВНАЯ
4,Усеченная разность
![]()
![]()
![]()
![]() общерекурсивная
общерекурсивная
5,Модуль разности
![]()
![]()
![]()
![]() 6,Факториальная
n!=1*2//(n-1)*n=
6,Факториальная
n!=1*2//(n-1)*n=![]()
Ф-ла 1ого разряда
1)0!=1
![]()
7,Минимум от(x,y)
![]()
![]()
![]() 8,Знак
числа
8,Знак
числа![]()
![]()
![]()
![]()
9,Остаток от целочисленного деления
![]()
![]()
![]()
2) (x,y+1)=prod(s( (x,y)),sg( | x -s( (x,y))| )
(29)![]() исчисление
– это безтиповая теория, которая
рассматривает функции, как правила, а
не как графики. В традиционном подходе:
два представления
исчисление
– это безтиповая теория, которая
рассматривает функции, как правила, а
не как графики. В традиционном подходе:
два представления
![]()
![]() выражают одну и ту же функцию, а с точки
зрения
исчисления
они выражают разные функции, так как
правила вычисления различны.
исчисление
– это прикладное исчисление предикатов
1-го порядка (ПИП 1-го порядка).
выражают одну и ту же функцию, а с точки
зрения
исчисления
они выражают разные функции, так как
правила вычисления различны.
исчисление
– это прикладное исчисление предикатов
1-го порядка (ПИП 1-го порядка).
ОСОБЕННОСТИ:
Безтиповость: объекты могут являться функциями и аргументами, т.е. функции могут быть заданы программами (функции или процедуры Pascal), которые могут передаваться через формальные параметры другим программам.
исчисление представляет класс частичных функций – «
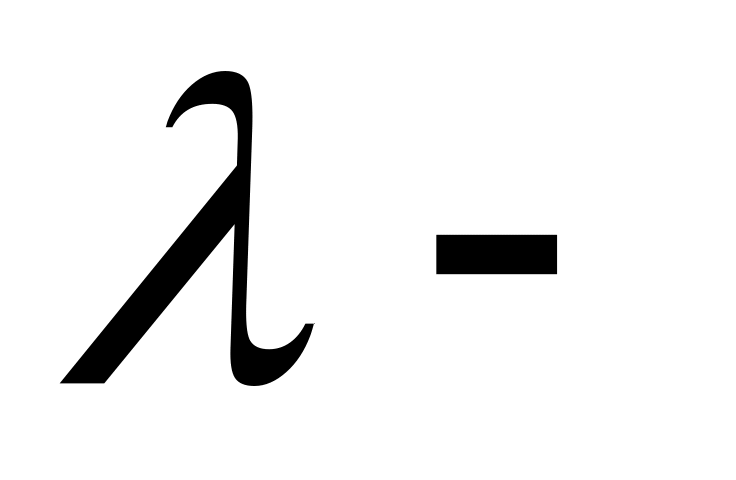 определимые
функции», которые характеризуют
неформальное понятие «эффективной
вычислимости», тем самым связано с
понятием «алгоритма вычисления».
определимые
функции», которые характеризуют
неформальное понятие «эффективной
вычислимости», тем самым связано с
понятием «алгоритма вычисления».исчисление является теоретической моделью современного функционального программирования (например, язык ЛИСП, который использует исчисление в качестве промежуточного кода после 1-го этапа трансляции).
выражения и их вычисления.
Пример:
![]() .
В
исчислении
различают (устраняют различное понимание):
символьную запись
.
В
исчислении
различают (устраняют различное понимание):
символьную запись
![]() и ее вызов (вычисление)
и ее вызов (вычисление)
![]() .
.
исчисление
изучает функции и их аппликативное
поведение (поведение относительно
применения к аргументу). Выражение
![]() можно считать как функцию от
можно считать как функцию от
![]() (это записывается как
(это записывается как
![]() )
и как функцию от
)
и как функцию от
![]() (это записывается как
(это записывается как
![]() ).
Вызовы могут быть следующими:
).
Вызовы могут быть следующими:
а)
![]() и
и
![]() ;
;
б)
![]()
в)
![]()
(30) Определение термов и выражений
ОПРЕДЕЛЕНИЕ:
Каждая переменная или константа есть терм.
По любой переменной и любому
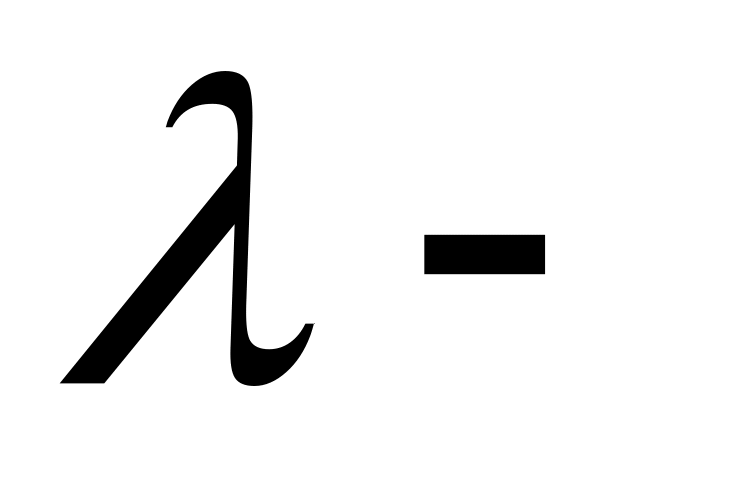 терму
M строится новый
терм:
терму
M строится новый
терм:
 –
функция от
,
которую называют
абстракцией.
–
функция от
,
которую называют
абстракцией.
Замечание
1: Аналогичен
в Pascal селектор записи «![]() ».
».
Замечание 2: Константы: целые числа, булевы константы, арифметические операции (функторы), булевы функции и т.п.
По любым термам M и N строится новый терм MN, обозначающий применение (аппликацию) оператора M к аргументу N, то есть подстановка
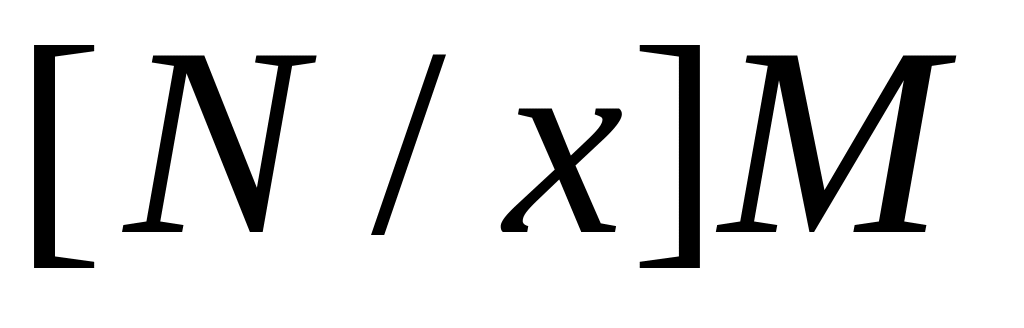 позволяет получать
выражения
(предикаты).
позволяет получать
выражения
(предикаты).
Замечание 3:Это определение термов (выражений) является правилом конструирования формул «по индукции».
Замечание 4: Правила вывода определяют алгоритм вычисления выражений
![]() СВОРАЧИВАНИЕ,
СВОРАЧИВАНИЕ,
![]() СВОРАЧИВАНИЕ
И РЕДУКЦИЯ
СВОРАЧИВАНИЕ
И РЕДУКЦИЯ
Определение 1: Константа, обозначающая функтор, применяемый к операндам, определяет подтерм, называемый редексом, а процесс применения называется сворачиванием, в результате которого получается новое выражение.
ПРИМЕР:
![]() То есть, «
То есть, «![]() »
–
редекс,
сворачивание:
»
–
редекс,
сворачивание:
Определение
2: Терм вида
![]() называется
редексом.
называется
редексом.
Определение
3: Если
редекс
содержится в терме
![]() и одно из его вхождений заменяется
термом (подстановкой)
,
то этот процесс
сворачивания
(свертывания) обозначается
и одно из его вхождений заменяется
термом (подстановкой)
,
то этот процесс
сворачивания
(свертывания) обозначается
![]() и означает, что терм
сворачивается
к
выражению
и означает, что терм
сворачивается
к
выражению
![]() .
.
Определение
4: Конечная
последовательность
или
свертываний
называется «редукцией».
Один шаг
или
свертывания
обозначается стрелкой без индекса,
просто «![]() ».
».
Замечание 5: Использование констант и правил излишне, так как константы можно реализовать только атомарными термами в виде переменных (т.е., «чистое исчисление» -
исчисление без констант и правил).
Примеры редукций (используемые редексы подчеркнуты):
1.
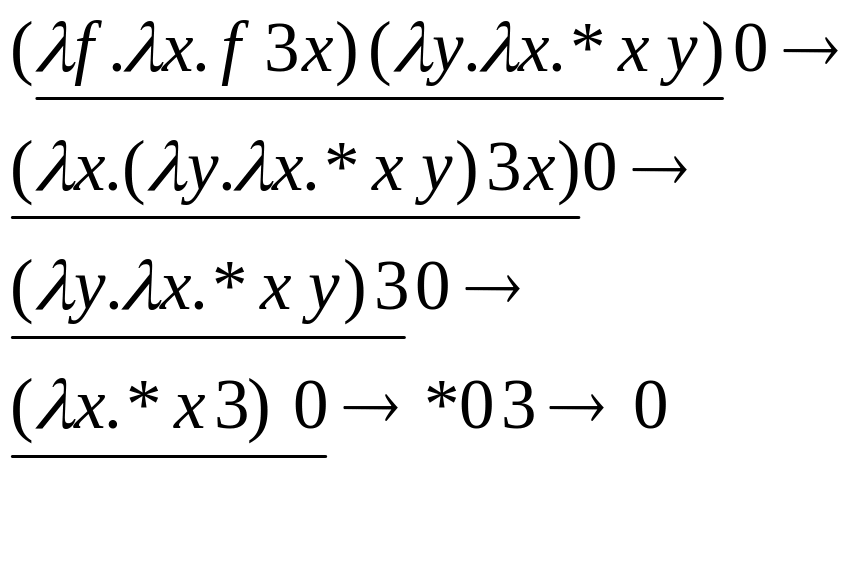
2.
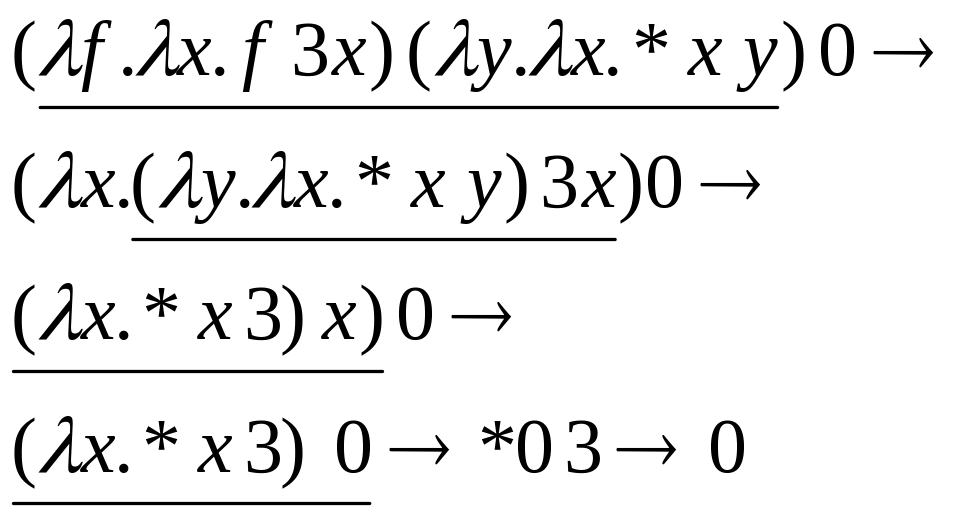
(31) Нормальные формы выражений
Определение: Если для выражения нельзя применить никакого правила редукции, т.е. выражение не содержит редексов и находится в «нормальной форме».
Замечание 1: В программировании этому понятию соответствует понятие конца вычислений по определенной синтаксической схеме, например:
While-(существует хотя бы один редекс) – do – (преобразовывать один из редексов) – end – (выражение теперь в нормальной форме).
Замечание 2: свертывания не всегда могут давать желаемый результат – может происходить зацикливание.
ПРИМЕР:
а)
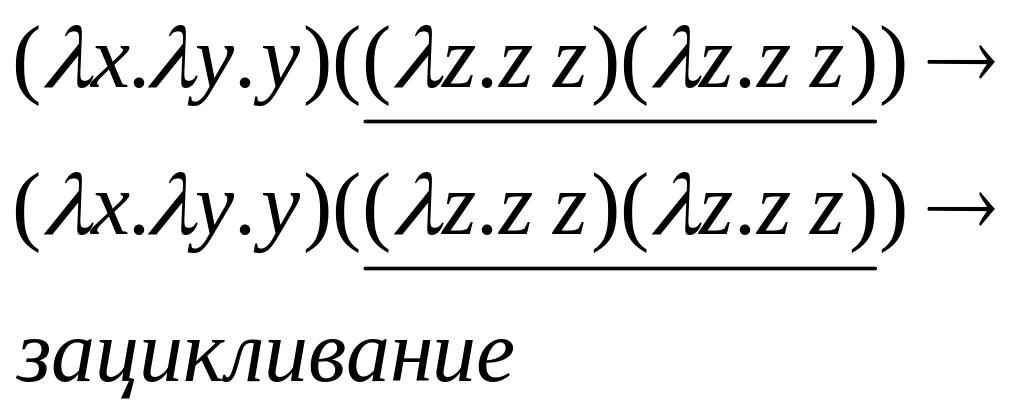
б)
![]()
