3.3.2 Ітераційні методи і їх реалізація в пакеті MatLab

Ітераційними методами вирішення систем лінійних рівнянь виду

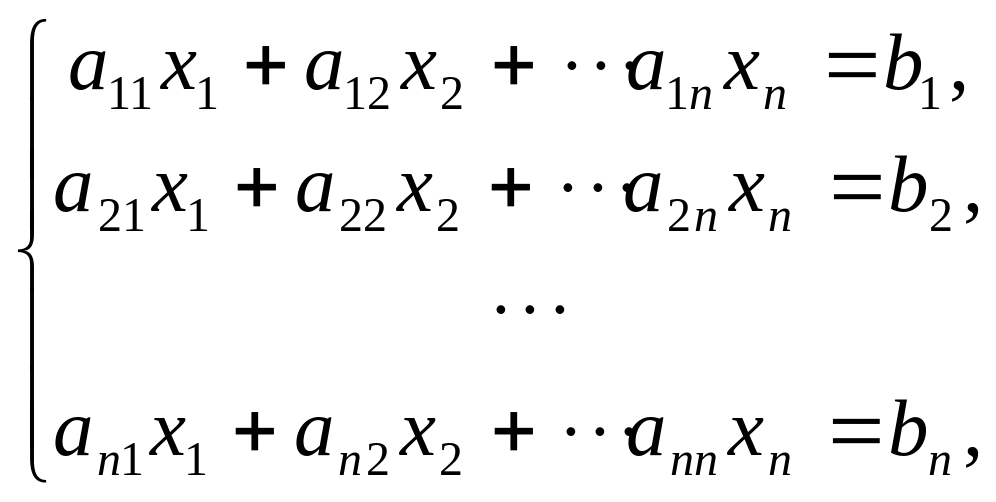
називаються методи, що дають вирішення системи рівнянь як межу послідовності наближень, що обчислюються за одноманітною схемою.

Ітерація Якобі:

для i=1,2,…,n.

Ітерація Зейделя:

для i=1,2,…,n.

Достатньою умовою збіжності ітераційних процесів і в методі Якобі, і в методі Зейделя є умова домінування коефіцієнтів що стоять на головній діагоналі:

для i=1,2,…,n.

Приклад 3.3. Розглянемо систему лінійних рівнянь

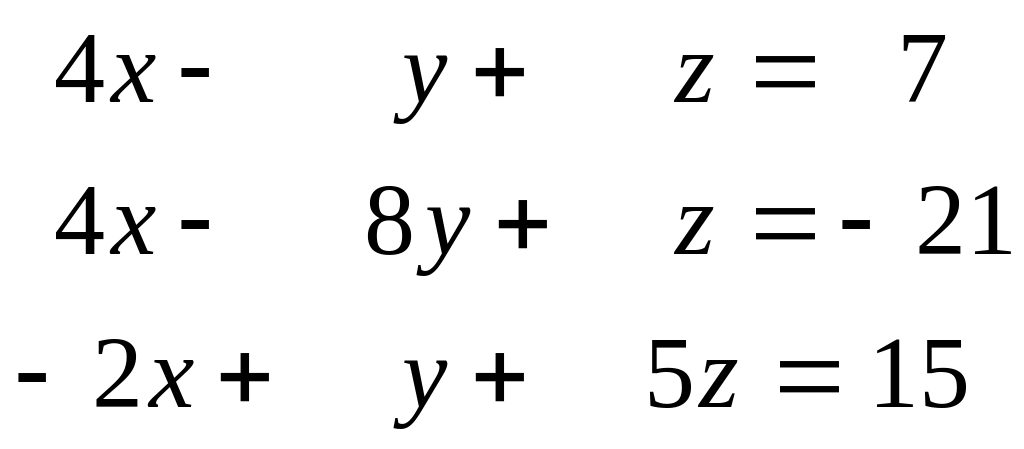
Точне рішення:

>> a=[4 -1 1;4 -8 1; -2 1 5]; b=[7;-21;15];

>> x=a\b

x =

2

4

3

Итерація Якобі: Рівняння запишим у виді

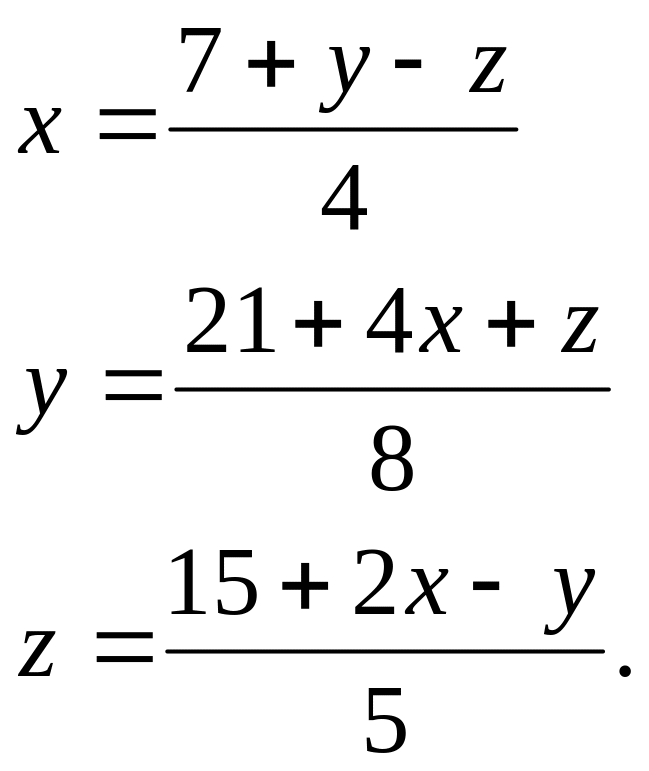
Це дозволяє запропонувати слідуючий ітераційний процес Якобі:

Покажемо, що якщо почати з точки, , то ітерації сходяться до розв’язку(2;4;3).

Підставимо в праву частину кожного рівняння, щоб набути нових значень:

Нова точка ближче до (2;4;3), чим P_0. Ітерації, що використовують ітераційні формули Якобі, генерують послідовність точок P_к. , яка сходиться до розв’язку(2;4;3).

Цей процес називається ітерацією Якобі і може використовуватися для вирішення лінійних систем. Після 19-і ітерацій послідовність наближених рішень сходиться до наближення з дев'ятьма значущими цифрами (4.00000000; 4.00000000; 3.00000000). Лінійні системи з такою великою кількістю змінних, як 100000, часто виникають при розв’язуванні диференціальних рівнянь із частинними похідними.

Ітерація Зейделя

Метод можна розглядати як модифікацію методу Якобі. Основна ідея полягає в тому, що при обчисленні чергового (k+1)-го наближення до невідомого x_i при i >1 використовують вже знайдені (k+1)-е наближення до невідомих x₁, x₂, ..., x_i-1, а не k-е наближення, як в методі Якобі.

Ітеративний процес Зейделя запишемо в наступному виді::

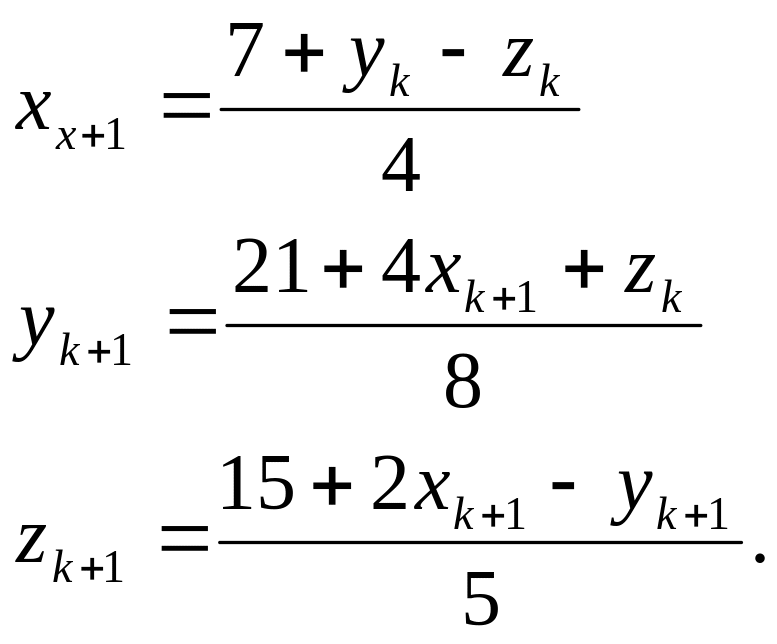
Покажемо, що якщо почати з точки , то ітерації сходяться до розв’язку(2;4;3).

На першій ітерації одержуємо:

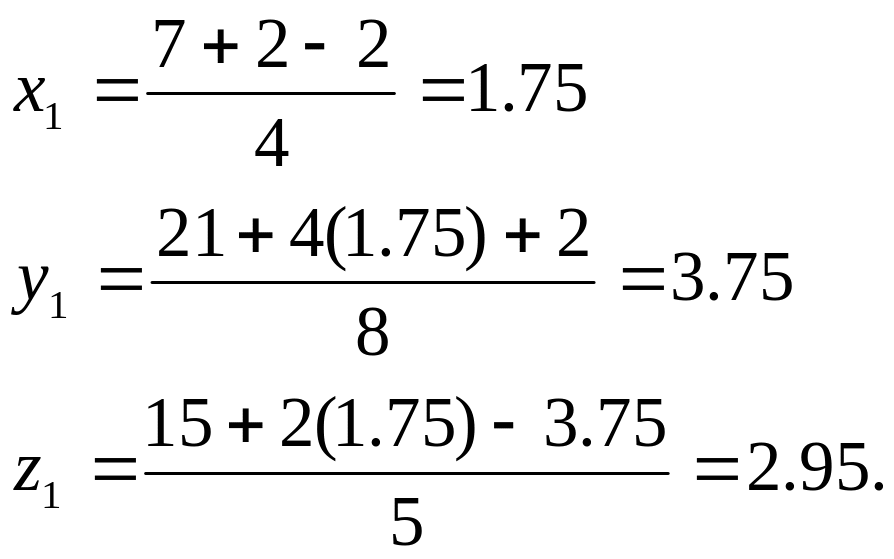
Нова точка ближче до (2;4;3), чим Р₀ , і краще, ніж значення, отримане в методі Якобі на першій ітерації. Для запропонованої СЛАР розв’язання методом Зейделя одержуємо за 10 ітерацій (у методі Якобі було потрібно 19 ітерацій).

Закінчення ітераційного процесу

Слід дати визначення близькості двох векторів так, щоб можна було ввести поняття збіжності послідовності наближень {P_k} до розв’язку P.

Найбільш використовуваними є наступні дві норми:

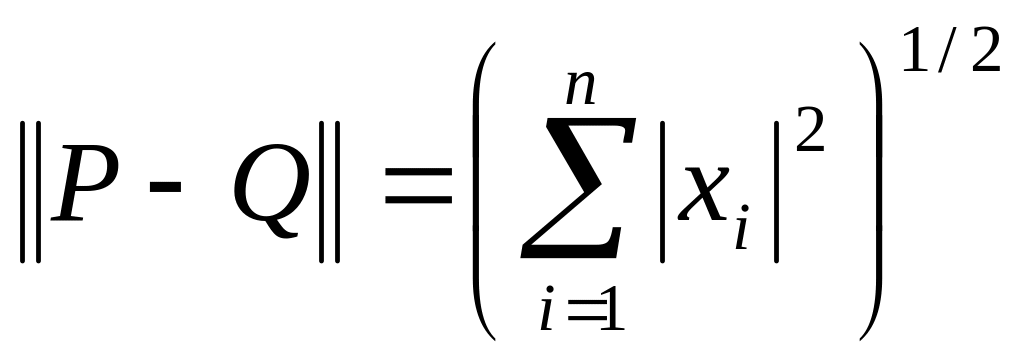- відстань Евкліда між і .

- норма, що вимагає менше зусиль для обчислень.

Т.ч. для заданої допустимої похибки ε>0 критерій закінчення ітераційного процесу можна записати у вигляді:

< ε,

або:

< ε.

Система MatLab має команду norm, яка є нормою Евкліда. Докладну інформацію про використання команди norm| можна прочитати в системі Help програми MatLab.

Лістинг програми 3.1 (ітерація Якобі). Розв’язання системи Ax=b, починаючи з початкового наближення x=P₀, і генерування послідовності {P_k} , котра сходиться до розв’язку. Ефективною умовою для застосування методу є те, що А – строго діагонально домінуюча матриця.

function [x,k]=jacobi(A,b,P,eps,maxiter)

%Input data – A – матриця розміру n*n

% - b – матриця розміру n*1

% - p – матриця розміру n*1, початкове наближення

% - eps – точність обчислень

% - maxiter – максимальне число ітерацій

%Output data – x – матриця розміру n*1: наближення Якобі до

% розв’язку Ax=b

n=length(b);

for k=1:maxiter

for i=1:n

x(i)=(b(i)-A(i,[1:i-1,i+1:n])*P([1:i-1,i+1:n]))/A(i,i);

end

err=abs(norm(x’-P));

P=x’;

if err<eps

break;

end

end

x=x’;

3.4 Індивідуальні завдання до лабораторної роботи

1. Обчисліть число обумовленості матриць А і С. Розв’яжіть системи засобами MatLab. Внесіть похибки до одного елементу матриці і в один елемент вектора правої частини. Знов розв’яжіть системи і порівняйте отримані розв’язки. Запишіть оцінки похибок.

2. Розв’язати систему Cx=D використовуючи формули Крамера.

3. Перевірити програми розв’язання СЛАР методами а) Якобі; б) Зейделя для заданих систем лінійних алгебраїчних рівнянь.

4. Виконати розрахунки з різною точністю, обчислюючи необхідне число ітерацій. Побудувати графіки залежності числа ітерацій від точності для різних методів.

Таблиця 3.1 – Варіанти завдань

№1	A B 1 0.47 -0.11 0.55 .3.33 0.42 1 0.35 0.17 3.29 -0.25 0.67 1 0.36 4.11 0.54 -0.32 -0.74 1 0.10	C D 1 2 3 13 2 3 5 4 3 5 9 17
№2	0.63 1 0.11 0.34 4.08 0.17 3.18 -0.45 0.11 0.17 0.31 -0.15 3.17 -4.35 3.28 0.58 0.21 -3.45 -3.18 0.05	1 2 3 0.55 1 4 9 3.35 1 8 27 3.55
№3	0.77 0.04 -0.21 0.18 3.24 -0.45 3.23 -0.06 0 -0.88 -0.26 -0.34 3.11 0 0.62 -0.05 0.26 -0.34 3.12 -3.17	0.42 3.43 0.27 1 3.43 -0.84 0.93 2 0.27 0.93 -0.48 3
№4	0.79 -0.12 0.34 0.16 -0.64 -0.34 3.18 -0.17 0.18 3.42 -0.16 -0.34 0.85 0.31 -0.42 -0.12 0.26 0.08 0.75 0.83	0.64 0.54 -0.33 3 0.54 -0.92 0.24 2 -0.33 0.24 0.78 1
№5	-0.68 -0.18 0.02 0.21 -3.83 0.16 -0.88 -0.14 0.27 0.65 0.37 0.27 -3.02 -0.24 -4.23 0.12 0.21 -0.18 -0.75 3.13	0.5 3.77 0.39 3.5 0.84 3.79 0.95 4.5 0.24 3.03 -0.41 3
№6	-0.58 -0.32 0.03 0 -0.44 0.11 -3.26 -0.36 0 -3.42 0.12 0.08 -3.14 -0.24 0.83 0.15 -0.35 -0.18 0 3.42	0.19 0.51 0.86 0.35 0.51 0.32 0.95 0.42 0.86 0.95 -0.12 0.45
№7	-0.83 0.31 -0.18 0.22 3.71 -0.21 -0.67 0 0.22 -0.62 0.32 -0.18 -0.95 -0.19 0.89 0.12 0.28 -0.14 -1 -0.94	0.64 3.54 -0.33 0.3 3.54 -0.92 0.24 0.2 -0.33 0.24 0.78 0.1
№8	-0.87 0.27 -0.22 -0.18 -3.21 -0.21 -1 -0.45 0.18 0.33 0.12 0.13 -0.33 0.18 0.48 0.33 -0.41 0 -1 3.21	0.55 3.77 0.39 3.5 0.84 3.79 0.95 4.5 0.24 3.03 -0.41 3
№9	-0.81 -0.07 0.38 -0.21 0.81 -0.22 -0.92 0.11 0.33 0.64 0.51 -0.07 -0.81 -0.11 3.71 0.33 -0.41 0 -1 3.21	0.59 3.77 3.39 3.5 0.84 3.79 0.95 4.5 3.24 3.03 -0.41 3
№10	-1 0.22 -0.11 0.31 -4.7 0.38 -1 -0.12 0.22 3.5 0.11 0.23 1 -0.51 3.2 0.17 -0.21 0.31 -1 0.17	3.42 3.43 0.27 0.1 3.43 -0.84 0.93 0.2 0.27 0.93 -0.48 0.3
№11	-0.93 -0.08 0.11 -3.18 0.51 0.18 -0.48 0 0.21 -3.17 0.13 0.31 -1 -0.21 3.02 0.08 0 -0.33 -0.72 0.28	-0.93 -0.08 0.11 3.18 0.18 -0.48 0 0.21 0.13 0.31 -1 0.210
№12	-0.95 -0.06 -0.12 0.14 4.17 0.04 -3.12 0.08 0.11 3.4 0.11 0.12 0 3.03 0.8 0.34 0.08 -3.06 0.14 4.1	-1 -0.07 0.21 0.92 1 0.03 -0.42 0.92 -0.03 1 -0.04 3.2
№13	0 -0.19 0.27 -0.88 3.2 -0.33 -1 -0.07 0.21 0.92 0.11 0 3.03 -0.42 0.92 -0.92 -0.03 0 -0.04 3.2	-1 -0.07 0.21 0.92 0.07 0.03 -0.42 0.92 0.21 0.42 -0.04 3.2
№14	-0.88 -0.23 0.25 -0.16 3.24 0.33 0.03 -0.84 -0.32 -3.15 0.14 -0.66 -0.18 0.24 0.89 0.12 -0.05 0 -0.85 0.57	0.08 -0.12 -0.77 0.32 0.25 0.22 0.14 -1 -0.77 -0.14 0.06 -0.12
№15	0.12 -1 0.32 -0.18 0.72 0.08 -0.12 -0.77 0.32 0.58 0.25 0.22 0.14 -1 -3.56 -0.77 -0.14 0.06 -0.12 -3.21	0.08 0.25 -0.77 0.32 0.25 0.22 0.14 -1 -0.77 0.14 0.06 -0.12
№16	-0.86 0.23 0.18 0.17 3.42 0.12 -3.14 0.08 0.09 0.83 0.16 0.24 -1 -0.35 -3.21 0.23 -0.08 0.05 -0.75 -0.65	1 2 3 0.55 2 4 9 0.35 3 9 5 0.55
№17	76 21 6 -34 -142 12 -114 8 9 83 16 24 -100 -35 -121 23 -8 5 -75 85	1 2 4 0.55 1 4 16 3.35 1 8 64 3.55
№18	-83 27 -13 -11 142 5 -68 13 24 26 9 54 127 36 23 13 27 34 156 49	0.64 0.53 -0.33 3 0.53 -0.92 0.23 2 -0.33 0.23 0.78 1
№19	1 2 3 9 3.11 2 1 9 4 3.16 3 9 1 4 3.24 9 1 3 4 3.55	5 3 1 11 3 5 3 17 1 3 5 19
№20	-1 0.28 -0.17 0.06 -21 0.52 -1 0.12 0.17 117 0.17 -0.18 -0.79 0 0.81 0.11 0.22 0.03 -0.95 -0.72	11 12 13 13 12 13 15 4 13 15 19 17