1.2. Прикладные задачи
Задача управления запасами
Как правило, все торгующие организации (магазины или базы) в процессе своей деятельности создают запасы продаваемого товара. Держать малые запасы не выгодно, т.к. приходится часто их пополнять, неся излишние расходы при приобретении малых партий товара (аренда транспорта, оплата командировок и т.п.). С другой стороны, большие запасы требуют увеличения расходов на хранение. Найдем наивыгоднейшую величину запаса.
Введем следующие обозначения:
– величина запаса,
единица измерения величины запаса
– м3,
литры и т.д.;
h
– стоимость хранения единицы товара в
единицу времени (примем, что это год),
.
Допустим, что
;
– скорость
расходования товара (спрос),
.
Допустим, что
.
С
хема
расходования товара изображена на рис.
1.7.
Т
– время полного истощения запаса (время
одного цикла),
– текущий запас,
.
Q.
Согласно
схеме имеем:
, (1.31)
. (1.32)
Затраты на хранение в одном цикле
.
Учитывая (1.31) далее получим –
,
т.е.
. (1.33)
Затраты на приобретение запаса Q
, (1.34)
где k – единовременные не зависящие от Q затраты, например, аренда вагона; с – цена приобретения единицы товара.
Как следует из (1.33), (1.34), общие затраты за цикл
.
Затраты за один
год, т.е. за
циклов,
.
Согласно (1.32)
. (1.35)
Исследуем функцию (1.35) на экстремум. Первая производная
. (1.36)
Из необходимого
условия экстремума
,
т.е. условия
,
вытекает, что
. (1.37)
Для выяснения
того, какого рода локальный экстремум
имеет место в точке
,
рассмотрим достаточное условие, а именно
выясним, какой знак имеет вторая
производная
.
Согласно (1.36)
. (1.38)
Как вытекает из
(1.37), (1.38),
,
следовательно, при
величина годовых затрат
(1.35) достигает минимума. В теории
управления запасами
(1.37) известна как величина наиболее
экономичного запаса.
В заключение заметим, что аналогичная задача может быть решена и для некоторого производственного участка, где в качестве товара будут выступать, например, обрабатываемые детали. Известны и ряд других диктуемых практикой постановок и решений задач управления запасами, см., например, [13].
Оптимальная форма пожарного ведра
Т
ребуется
из металлической заготовки в форме
диска радиуса r
изготовить пожарное ведро. Для этого
достаточно вырезать из заготовки сектор
с раствором в
угловых единиц и затем придать оставшейся
заготовке форму конуса. Это и есть
пожарное ведро, рис. 1.8.
Вполне понятно, что существует некоторое значение , при котором объем конуса будет максимальным. Определим это .
Последовательно запишем:
,
,
,
объем ведра
. (1.39)
Найти такое значение , при котором объем V (1.39) достигает максимума.
Из необходимого
условия экстремума
вытекает, что
. (1.40)
Уравнение (1.40) имеет место, если
1)
или
2)
.
Первое условие не приемлемо, т.к. согласно (1.39) получим нулевой объем. Второе условие преобразуется к виду
,
откуда получаем два значения искомого угла:
,
.
Принимаем значение
.
В этом случае
,
т.е.
.
Достаточное условие можно не привлекать, т.к. решение очевидное.
Управление запасами скоропортящегося продукта [2].
Допустим, что
имеется некоторый запас Q
товара, который обладает определенным
сроком годности. Если к этому сроку
товар не будет продан, то остатки товара
следует продать по ликвидационной
стоимости. Будем считать, что спрос на
продукт – случайная непрерывная величина
с плотностью вероятности
.
Напомним, что
, (1.41)
где А – известная верхняя граница случайной величины X. Пусть
– стоимость
приобретения единицы товара,
– стоимость единицы
товара при продаже,
– потери на единицу
товара при отсутствии запаса,
– ликвидационная
стоимость товара.
Поясним, что представляют из себя потери при отсутствии запаса. При наличии товара заказчик переводит на счет предприятия соответствующую сумму. Эти деньги с той или иной степенью эффективности сразу же начнут «работать». При отсутствии запаса никаких перечислений, естественно, не будет. Кроме того, при отсутствии запасов необходимо нести определенные затраты, например, по поддержанию в рабочем состоянии пустующих складских помещений и т.п.
Из всего вышеуказанного следует, что возможно существование некоторой оптимальной величины запаса товара Q. Определим это Q.
Допустим, что товар
закуплен в размере Q.
Величина Q
подлежит
определению, однако, заранее известно,
что Q
– детерминированная величина и
.
Непрерывная
случайная величина X
имеет два варианта реализации –
и
.
В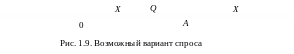
том случае, когда
(рис. 1.9), т.е. спрос X
меньше
количества приобретенного товара Q,
продан будет
товар в объеме X
по цене
с2,
а товар в количестве
будет продан по ликвидационной стоимости
4.
В таком случае случайная величина суммарных расходов и поступлений от продажи товара
,
, (1.42)
г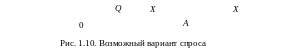
де
знак минус соответствует расходам, плюс
– поступлениям.
В том случае, когда (рис. 1.10), т.е. спрос X превысил количество закупленного товара Q, весь запасенный товар Q будет продан по цене с2. При этом предприятие понесет убытки из-за отсутствия товара при наличии спроса. Случайная величина суммарных затрат и поступлений опишется как
,
. (1.43)
В общем случае случайная величина затрат и поступлений связана с закупкой товара в количестве Q единиц и его продажей (рис. 1.10) как
(1.44)
Найдем математическое ожидание для случайной величины S(X). Как известно [3], математическое ожидание
,
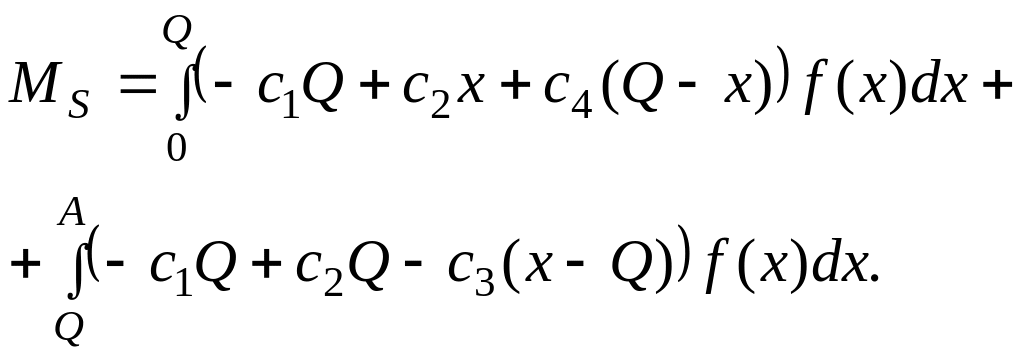(1.45)
Интегрируя, находим, что
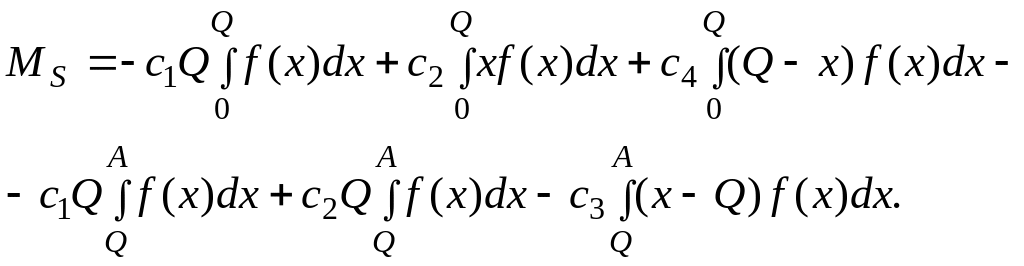(1.46)
Объединив первое и четвертое слагаемые, с учетом (1.41) далее получим:
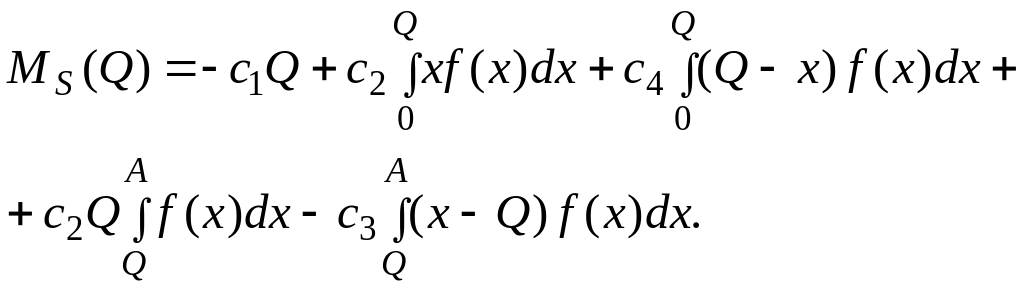(1.47)
Математическое
ожидание
является функцией величины Q,
т.е.
.
Опираясь на необходимое и достаточное
условия, исследуем эту функцию на
локальный максимум. Другими словами
выясним, не существует ли такая величина
исходного запаса Q,
при которой математическое ожидание
суммарных затрат и поступлений достигает
максимума.
Напомним [1], что для некоторой функции
,
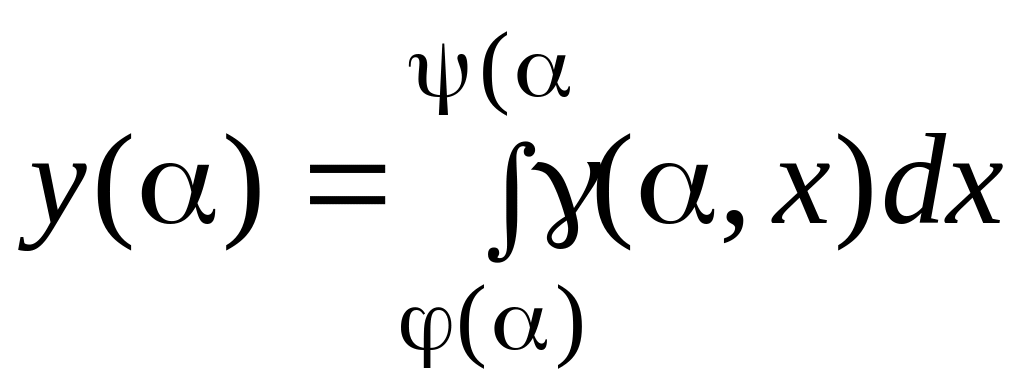где
– дифференцируемые функции, производная
.
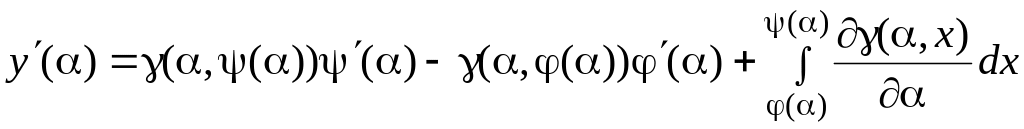Пример.
,
.
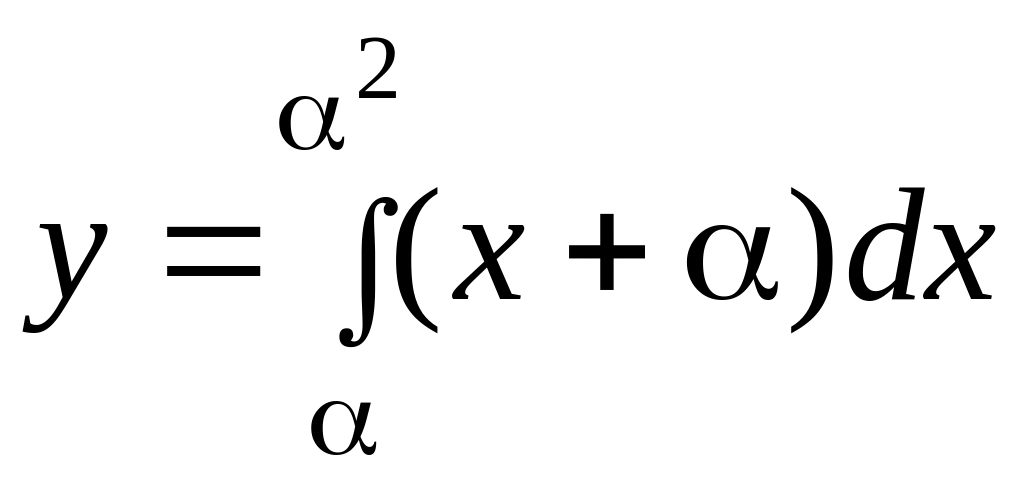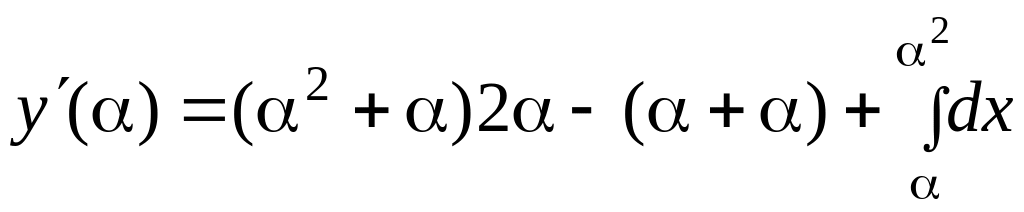Используя (1.47), запишем, что
,
; (1.48)
. (1.49)
Последнее выражение преобразуем к виду
. (1.50)
Как следует из
(1.48), необходимое условие максимума
дает следующее уравнение для определения
Q,
. (1.51)
Исследуем знак
второй производной
Поскольку f(x)
всегда не отрицательна, т.е.
,
следовательно,
,
если
. (1.52)
Итак, найденное из уравнения (1.48) значение Q обеспечит максимум целевой функции (1.47) при
. (1.53)
Как правило,
,
в таких случаях любое решение уравнения
(1.48) обеспечивает максимум целевой
функции (1.47). Подчеркнем, что значение
Q,
найденное из уравнения (1.48), обеспечит
максимум величины суммарных поступлений
и затрат не в отдельном случае (в разовой
закупке), а в среднем для массы закупок,
т.е. когда товар в объеме Q
единиц запасается много раз подряд.
Заметим, что теоретически возможен случай, когда
. (1.54)
В этом случае целевая функция (1.47) достигает минимума.
Рассмотрим частный случай. Пусть X подчинена закону равномерной плотности, т.е.
(1.55)
График этой зависимости приводится на рис. 1.12.
У
равнение
(1.51) в данном случае запишется как
,
откуда находим
. (1.56)
Значение Q (1.56) обеспечивает максимум целевой функции (1.47) при условии (1.53).