Глава I Безусловная оптимизация
Целевые функции одной переменной
Теоретические основы. Необходимые определения
-интервалом
точки
называется множество действительных
чисел x,
удовлетворяющих неравенству
,
(1.1)
г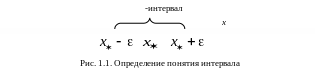
де
– конечное или бесконечно малое
положительное число. Это определение
следует понимать так, что если слева и
справа от некоторой точки
можно указать такие точки x,
для которых имеет место (1.1) (пусть даже
и бесконечно малое число), то это означает,
что точка
имеет
-интервал.
Обратим внимание на тот факт, что точки
и
-интервалу
не принадлежат. На рис. 1.1 изображен
-интервал.
Правым -полуинтервалом точки называется множество действительных чисел x, для которых имеет место неравенство
, (1.2)
где – конечное или бесконечно малое положительное число.
Левый полуинтервал определяется неравенством
. (1.3)
На рис. 1.2 изображены
левый и правый полуинтервалы. Условимся
интервал, левый полуинтервал и правый
полуинтервал обозначать соответственно
как
,
и
.
Р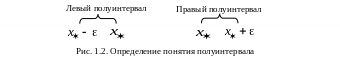
ассмотрим
некоторый интервал [a,b].
Точка x
является внутренней точкой этого
интервала, если
,
т.е.
.
Внутренняя точка интервала [a,b] называется точкой локального минимума функции f(x), если для этой точки можно указать такой -интервал, что
(1.4)
(
читается «для любых»).
Для внутренней точки локального максимума вместо (1.4) соответственно имеем
. (1.5)
Для интервала
[a,b]
точки
являются граничными точками. Точка
является точкой локального минимума
функции
,
если для этой точки может быть указан
такой полуинтервал
,
что
. (1.6)
Точка является точкой локального максимума функции , если для этой точки может быть указан такой полуинтервал , что
. (1.7)
Аналогичные
определения могут быть даны для граничной
точки
.
Точка называется точкой глобального минимума функции f(x) на интервале [a,b], если имеет место неравенство
. (1.8)
Для точки глобального максимума соответственно имеем
. (1.9)
Н
а
рис. 1.3 приведена функция, для которой
– точки локального максимума; a,
– точки локального минимума;
– точка глобального максимума;
– точка глобального минимума;
– точки как локального минимума, так и
локального максимума.
Внутренняя точка
интервала [a,b]
называется стационарной точкой функции
,
если в этой точке производная
.
Необходимое и достаточное условие локального минимума и локального максимума
Пусть функция
определена и
раз дифференцируема во всех точках
открытого интервала (a,b).
Пусть далее известно, что в точке
,
являющейся внутренней для интервала
[a,b],
функция f(x)
достигает локального минимума. Покажем,
что в таком случае точка
должна быть стационарной точкой, т.е.
. (1.10)
Заметим прежде всего, что поскольку – точка локального минимума, то по определению существует такой -интервал, что
(1.11)
Справа от точки
выберем произвольную точку
таким образом, чтобы она все же
принадлежала интервалу
(рис. 1.4).
Т
очку
закоординируем как
, (1.12)
где
– такое положительное число, что
. (1.13)
Воспользуемся формулой Тейлора [1] и запишем, что
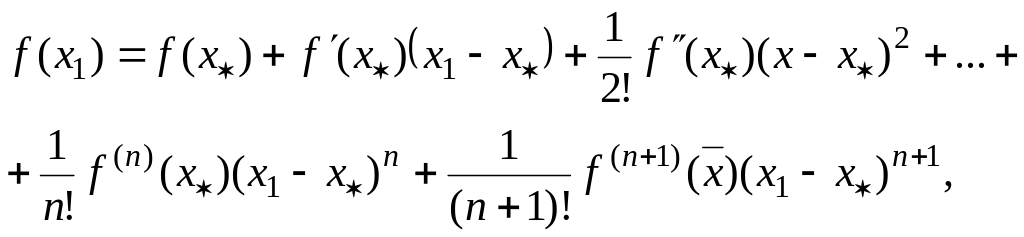(1.14)
где
.
Учитывая (1.12) далее запишем, что
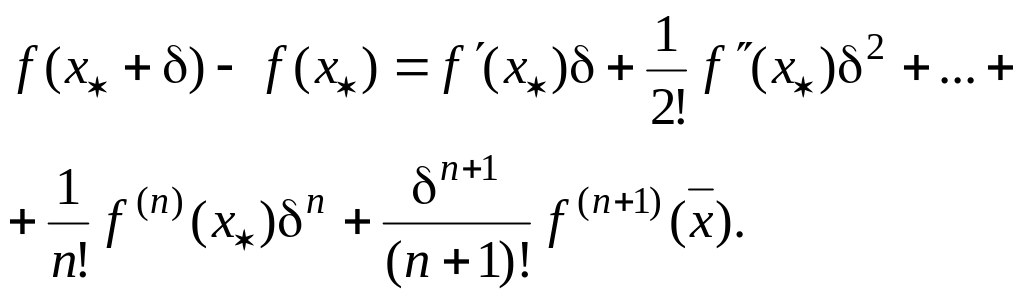(1.15)
Согласно (1.11) должно выполняться неравенство
,
а потому, как это следует из (1.15), должно быть так, что
. (1.16)
Допустимо считать, что число сколь угодно малое. Согласно (1.13) положительное число еще меньше, поэтому при достаточно малом первое слагаемое левой части выражения (1.16) будет доминировать над остальными слагаемыми, в таком случае
. (1.17)
Так как
,
то для выполнения неравенства (1.17) должно
быть
. (1.18)
Далее все рассуждения
можно повторить для точки
,
лежащей слева от точки
(см. рис. 1.4), т.е.
, (1.19)
где , как и в предыдущем случае, число положительное. Записав выражение (1.19) в виде
,
где
, (1.20)
и, повторив выкладки
(1.14) – (1.16), но уже для
,
установим, что для этой точки должно
быть
.
С учетом (1.20) далее имеем
. (1.21)
Итак, должны выполняться сразу оба неравенства – (1.18) и (1.21). Это возможно только лишь тогда, когда
. (1.22)
Условие стационарности точки доказано. Выражение (1.22) есть необходимое условие минимума функции f(x) во внутренней точке интервала [а,b].
Получим теперь
достаточное условие локального минимума
функции f(x)
во внутренней точке
.
Поскольку (1.22) имеет место, то (1.16) предстанет в виде
. (1.23)
Пусть
,
тогда при достаточно малом слагаемое
будет преобладать по абсолютной величине над остальными слагаемыми левой части выражения (1.23). В такой ситуации достаточно иметь
, (1.24)
чтобы выполнялось неравенство (1.23), т.е. чтобы в точке имел место локальный минимум. Итак, для того, чтобы функция во внутренней точке интервала [а,b] достигала локального минимума должны выполняться два условия – необходимое
(1.25)
и достаточное
. (1.26)
Совершенно аналогично можно доказать, что необходимое и достаточное условия локального максимума функции во внутренней точке интервала [а,b] имеют вид
, (1.27)
. (1.28)
Результаты (1.25) –
(1.28) получены в предположении, что
.
В том случае, когда
,
в левой части выражения (1.23) анализу
подвергается слагаемое
.
Если
,
то в точке
– точка перегиба функции f(x).
Это заключение вытекает из того факта,
что слева и справа от точки
разность
будет менять свой знак на противоположный (не выполняется ни условие локального минимума (1.4.), ни условие локального максимума (1.5)).
Если
,
то следует анализировать производную
и т.д.
Условимся в дальнейшем операцию отыскания локального минимума или максимума во внутренних точках интервала [а,b] называть исследованием функции на экстремум.
Пример 1. Исследовать на экстремум функцию
,
где а – некоторая константа.
Записываем производные
,
(1.29)
Необходимое условие экстремума функции в данном случае записывается как
.
Отсюда вытекает,
что в точке
«подозревается» наличие экстремума,
т.е. локального минимума или локального
максимума. Не исключается и возможность
наличия в точке
точки перегиба. Поскольку, как это
следует из (1.29), в этой точке
,
то, согласно (1.26),
функция
в точке
достигает локального минимума.
Пример 2. Исследовать на экстремум функцию
,
.
Имеем
.
Из необходимого
условия экстремума
вытекает, что
,
.
Далее находим, что
,
следовательно, точка
– точка локального минимума,
,
следовательно, точка
– точка локального максимума.
Пример 3. Исследовать на экстремум функцию
В данном случае
.
И
сследуя
необходимое и достаточное условия,
устанавливаем, что в точке
функция
имеет точку перегиба, рис.1.5.
Замечание.
Требование дифференцируемости функции
весьма существенно. Если функция
не дифференцируема, например, в точке
локального минимума, то рассмотренный
выше метод исследования функции на
экстремум не проходит. Например, пусть
(1.30)
Г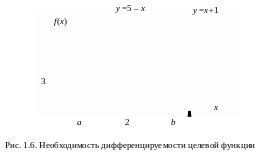
рафик
этой функции приводится на рис. 1.6.
Функция
в точке
достигает локального минимума, однако
установить этот факт с помощью необходимых
и достаточных условий не представляется
возможным, т.к. производные функции
(1.30) в точке
не определены.
Теорема.
Пусть в точке
первые
производные функции
обращаются в ноль, а производная n-го
порядка отлична от нуля.
Если n – нечетное, то – точка перегиба.
Если n – четное, то – точка локального экстремума, причем, если эта производная >0, то – точка экстремума-минимума, если <0 – экстремума-максимума.
Доказательство приводить не будем, лишь только заметим, что оно осуществляется в том же ключе, что и доказательство условий (1.25) – (1.28). Интересующихся этим доказательством отсылаем к источнику [2].
Пример. Исследовать на экстремум функцию
,
.
В данном случае
,
,
и результат исследования стационарных точек отражает табл. 1.
Таблица 1
Стационарные точки
|
|
|
|
min, max или т/п |
0 |
36 |
0 |
– 360 |
т/п |
1 |
27,5 |
60 |
– |
min |
2 |
44 |
–120 |
– |
max |
3 |
5,5 |
540 |
– |
min |
В приведенной таблице т/п означает «точка перегиба», а прочерки указывают на то, что в данных значениях нет необходимости.