
- •Глава I Безусловная оптимизация
- •Теоретические основы. Необходимые определения
- •Необходимое и достаточное условие локального минимума и локального максимума
- •Задача отыскания глобального минимума
- •Рубежный тестовый контроль
- •1.2. Прикладные задачи
- •Оптимальная форма пожарного ведра
- •Рубежный тестовый контроль
Задача отыскания глобального минимума
Пусть требуется
указать такую точку
![]() ,
в которой функция
,
где
,
в которой функция
,
где
![]() ,
достигает глобального минимума.
,
достигает глобального минимума.
Точка глобального минимума отыскивается путем сравнения значений всех локальных минимумов и значений функции в граничных точках, т.е. в точках и . Если – дифференцируемая функция во всех точках , то точка может отыскиваться путем сравнения значений функции в тех стационарных точках, в которых f(x) достигает локального минимума и значений f(a) и f(b). На практике, однако, при отыскании классификацию стационарных точек на точки минимума и максимума не проводят и точку глобального минимума находят путем сравнения значений функции f(x) во всех стационарных точках и значений f(a) и f(b).
Пример.
Указать точку глобального минимума
функции
,
![]() .
Сравнивая между собой значения функции
(см. Таблицу 1)
.
Сравнивая между собой значения функции
(см. Таблицу 1)
![]()
![]()
![]()
![]()
![]()
![]() ,
устанавливаем, что
,
устанавливаем, что
![]() .
.
Рубежный тестовый контроль
Точка имеет -интервал на интервале [a,b], если
слева и справа от могут быть указаны точки, принадлежащие интервалу [a,b];
хотя бы слева от имеются точки, принадлежащие интервалу [a,b];
хотя бы справа от имеются точки, принадлежащие интервалу [a,b];
кроме можно указать хотя бы одну точку, принадлежащую интервалу [a,b].
Точка имеет полуинтервал на интервале [a,b], если
слева от или справа от могут быть указаны точки, принадлежащие интервалу [a,b];
только слева от имеются точки, принадлежащие интервалу [a,b];
только справа от имеются точки, принадлежащие интервалу [a,b];
или только слева или только справа от могут быть указаны более одной точки, принадлежащей интервалу [a,b].
Точка называется точкой локального минимума, если для этой точки
может быть указан интервал или полуинтервал, для которого
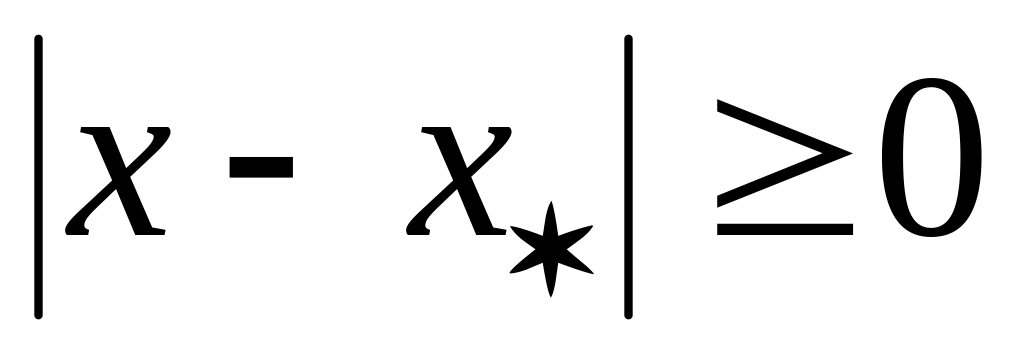 ;
;может быть указан такой интервал или полуинтервал, для каждой точки x которого
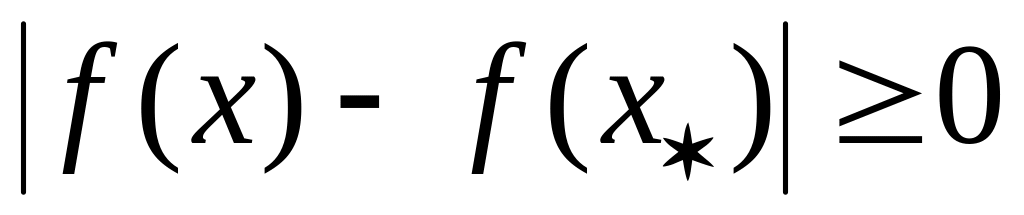 ;
;может быть указан интервал, для которого
 ;
;может быть указан хотя бы полуинтервал, для каждой точки которого
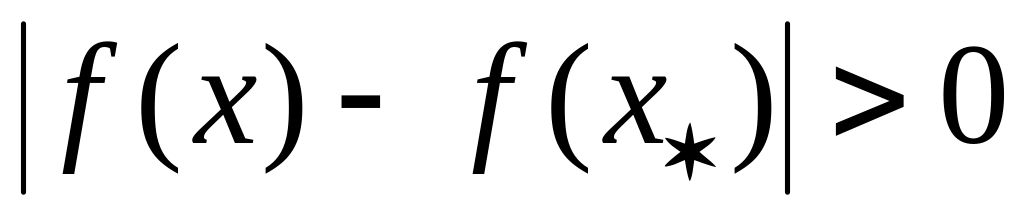 .
.
Точка является точкой глобального минимума, если
имеет место неравенство ;
на интервале [a,b] имеет место неравенство
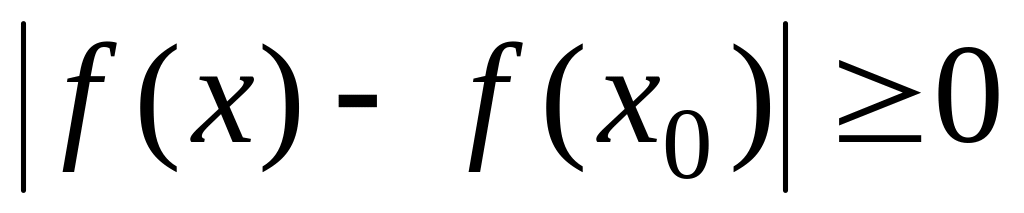
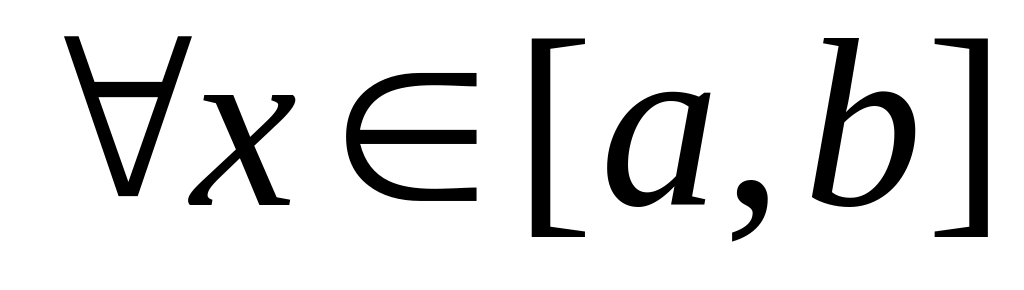 ;
;имеет место неравенство
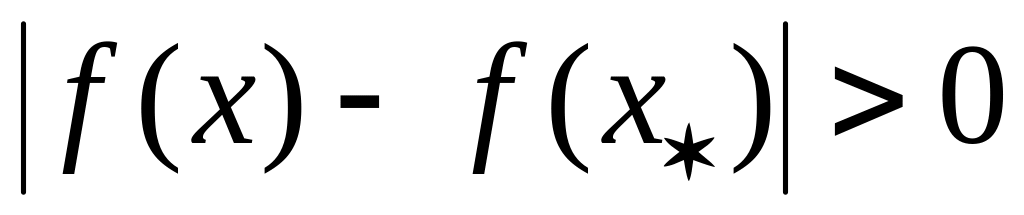 ;
;среди всех локальных минимумов, имеющих место на интервале [a,b], принимает наименьшее значение.
Точка называется стационарной точкой функции , если
1) имеет вполне определенное значение;
2)
![]() ,
;
,
;
3)
,
![]() ;
;
4) .
6. Функция
![]() достигает экстремума в точке
на интервале [a,b],
если
достигает экстремума в точке
на интервале [a,b],
если
1)
![]()
![]() ;
;
2)
![]() ;
;
3)
![]() ,
,
![]() ;
;
4) .
7. Необходимое условие экстремума функции в точке записывается как
1)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
;
4)
;
![]() .
.
8. Достаточные условия локального минимума записываются как
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)![]() ;
4)
;
4)
![]() .
.
9. При отыскании
глобального минимума функции
![]() на интервале [a,b]
следует
на интервале [a,b]
следует
1) воспользоваться необходимым и достаточным условиями;
2) среди всех локальных минимумов найти наименьший;
3) среди всех
локальных минимумов и
![]() ,
,
![]() найти наименьшее значение;
найти наименьшее значение;
4) использовать условия , и принять во внимание значения , .
