16. Синтез инвариантных системм упр-ния.

З адачи инвариантности-обеспечение независимости каких-то координат от возмущающих воздействий.

Пусть сис-ма опис-ся сис-ой ур-й:

a11x1+a12x2+a13x3=ν(t);

a21x1+a22x2+a23x3=0;

a32x2+a33x3=0. На основании ур-й м. составить стр-ю сх-му, позвол-ю нах-ть переменные x:

Из сх. видно, что возмущение ν(t) напрямую влияет на корд-ту x1. При такой стр-ре сис-мы почти невозможно обеспечить инвар-ть координаты x1. Изменим порядок ур-й:

a21x1+a22x2+a23x3=0;

a32x2+a33x3=0

a11x1+a12x2+a13x3=ν(t);

Сост-м новую стр-ю схему:

В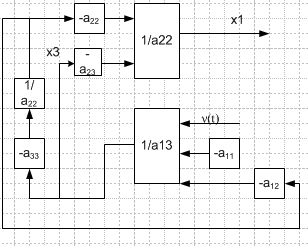 торая стр-я сх. им-т два

Канала для направления

возд-й от возмущения ν к переменной х1. Наличие 2

каналов позволяет

организ-ть прох-е возмущ-я

т.о., ч/бы суммарный эф-т

от возмущ-я сводился к нулю(пр-п двухканальности).

Возьмем одноконтурную систему:

В данной сис-ме возмущение доступно измерению, что позвол-т ис-но создать 2 канал для прох-я возмущения на выход сис-мы:

У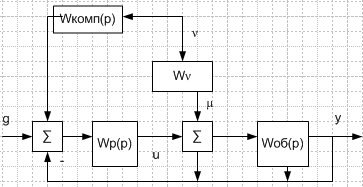 словие компенсации на основании стр-ой схемы:

νWкомп(p)Wр(p)=νWν(p);

Wкомпен-ра(p)= Wν(p)/ Wр(p);

17. Многосвязные лин-е системы и их анализ.

Многосв-й объект управ-я сод-т m управ-х каналов и n выходов.

В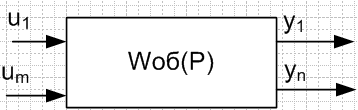 этих сис-х присут-т взаимосвязь каналов. Учет взаимосвязи каналов яв. одним из важнейших требований при синтезе систем управления такими объектами. Для этого восп-ся м-дом Бристоля, кот. закл-ся в постр-и спец-ой матрицы:

элементы кот-ой в статике соот-т соотношению λ_1j=(dy_i/du_j)/(dy_i/du_j)_c (все контуры разомкнуты/все контуры, кроме u_c, замкнуты), где yi-уст-ся значение i-го выхода, uj-управление. Необходимо опр-ть коэф-ты перед-й матрицы:

Затем надо найти элементы матрицы: [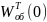 ]^-1

Эл-ты матрицы Λ нах-ся из выражения: ^-1ij путем перемнож-я эл-тов с одинак-ми индексами. Анализ мат-рицы Λ показ-т, что сис-ма имеет слабую связан-сть, если диаг-е эл-ты близки к ед-це, а недиаг-е сущ-но меньше (близки к 0). 1н из первых м-дов синтеза систем был основан на компенс-и или развяз-и перектестных связей объекта и получил название автоном-го рег-ния. Авт-е рег-е обесп-т раздельное упр-ние вых-ми объекта за счет вкл-я в состав системы компенсатора, напр., м/ду рег-ром и объектом. Перед-я матрица расширенного объекта равна: Wоб(p)Wк(p)=Wр.об.(p). В кач-ве эл-тов передаточной матрицы расшир-го объекта принимаются диагональные элементы передаточной матрицы исх. объекта:

Wр.об.=W011(p) 0 0 … 0

0 W022(p) 0 … 0

. . . . .

. . . . .

0 0 0 … W0nn(p)

Или Wр.об.(p)=diagWоб(p)

Тогда м. найти передаточную матрицу компенсатора:

Wk(p)=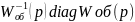 Получ-е матем-м путем рез-ты треб-т оценки из усл-й их физ-ой реализ-сти.

18. Синтез многосв-х лин-х систем с исп-м модального упр-я и компенсаторов.

Задача: при известных дин-х хар-х объекта упр-ния, зад-х соотв-ми перед-ми матрицами, опр-ть стр-ру и эл-ты матрицы рег-ра т.о., ч/бы при устан-х воздей-х хар-р перехода сис-мы в новое установ-ся состояние минимально отличался от заданного.

Пусть S(p) - n-мерная вектор-фун-я зад-х вых-х хар-к сис-мы при станд-х вых-х сиг-х. в кач-ве вх-х сиг-в примем единичный скачок. В кач-ве обобщ-х динам-х хар-к м. исп-ть изображения переходных хар-к:

S1(p)= k_i(a_ip+d_i) / p(b_ip²+c_ip+l_i)(γ_ip+1) (1)

C учетом передаточной матрицы объекта и вых-х хар-к (1) м. найти вектор операторов на входе в объект или вых-в рег-ра:

U(p)=[Wоб(p)]^-1S(p)

П усть сис-ма им-т стр-ю сх. изображ-ю на рис-ке:

Если при синтезе сис-мы исп-ть скачкообр-е вх-е сигналы, то получаем:

ε(p)=(1/p)[I-S(p)]

Зная u(p) и ε(p) м. найти передаточную матрицу регулятора:

Wp(p)=[(1/p)I-S(p)]^-1[Wоб(p)]^-1

19. М-ДЫ ФАЗОВОЙ ТРАЕКТОРИИ ПРИ ИССЛЕД-И НЕЛИН-Х СИСТЕМ.

В общем случае нелинейную систему можно описать системой нелинейных дифференциальных уравнений в нормальной форме: , (3.18)

где x_i – корд-ты сост-я системы; g(t) – задающее воздействие.

Для систем с постоянными параметрами при отсутствии задающего воздействия и не нулевых начальных условиях уравнение (3.18) перепишем в виде 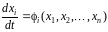. (3.19)

В пр-ве координат x₁, … , x_n можно представить графически реш-е в виде некот-й кривой, называемой фазовой траекторией.

Для системы второго порядка: 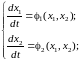(3.20)

можно исключить время и тогда 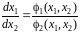. (3.21)

Точки равновесного состояния системы определяются нулевыми значениями скорости dx₁/dt = dx₂/dt = 0, что соответствует 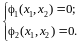(3.22)

Точки равновесного состояния системы называются особыми точками на фазовой траектории. При переходе от области одной особой точки к области другой особой точки может существенно меняться поведение системы, что требует глубокого анализа нелинейной системы в зоне особых точек. В окрестности особых точек можно построить значительное число фазовых траекторий, семейство которых называют фазовым портретом.

Пусть имеем линейную систему второго порядка:

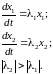(3.23)

Решение этих ур-й имеет вид: (3.24)

и, исключив t из решения, имеем: 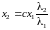. (3.25)

Особая точка для этой системы: . (3.26)

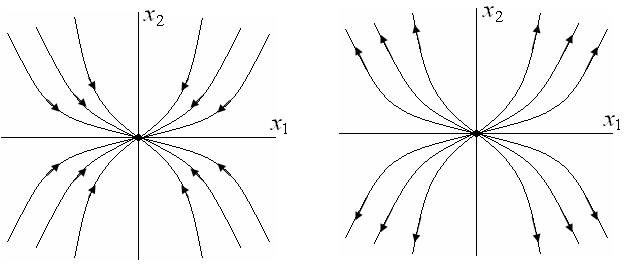
х₂

х₁

а)

б)

Рис. 3.11. Фазовые траектории для случаю веществ-х корней

одного знака: а) λ₁ < 0, λ₂ < 0; б) λ₁ > 0, λ₂ > 0

Рис. 3.12. Фазовые траектории для случая вещественных корней разного знака

Если корни комплексные (3.27)

то фазовые траектории в зависимости от знака при коэффициенте α имеют следующий вид (рис. 3.13).

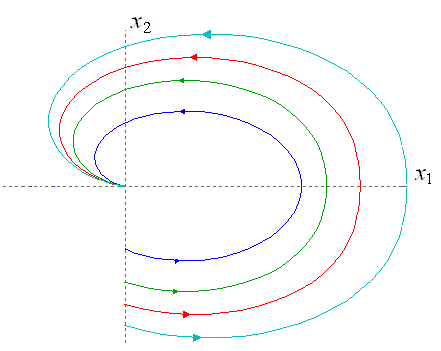
Рис. 3.13. Фазовые траектории при комплексных корнях: а) α < 0;

Если корни чисто мнимые 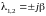, (3.28), то

. (3.29)

Возведем в квадрат x₁ и x₂ и, сложив получ-е уравнения, найдем:

. (3.30). Фазовые траектории, соотв-е данному уравнению, имеют вид эллипсов (рис. 3.14).

Приведенные фазовые портреты получили следующие названия: узел (рис. 3.11), седло (рис. 3.12), фокус (рис. 3.13), центр (рис. 3.14). Фазовые портреты узел и фокус подразделяются на устойчивые, если траектории стремятся к особой точке, и на не устойчивые, если траектории уходят от особой точки.

Рис. 3.14. Фазовые траектории для системы с мнимыми корнями

20. М-Д ГАРМОНИЧ-СКОЙ ЛИНЕАРИЗАЦИИ И ЕГО ИСП-Е ПРИ АНАЛИЗЕ И СИНТЕЗЕ СИСТЕМ УПР-НИЯ.

М-д гармонич. линеаризации-осн-н на том, что в силу фильтрующих или резонансных св-в сис-мы, дв-е в кот-ой близко к синусоидальному, при исследовании периодического режима м. принимать во внимание только основную гармонику. Пусть замкнутая с-ма состоит из нелин-го безынерционного эл-та с хар-ой: ξ=φ(σ) (1) и инерц-ой линейной части, описываемой комплексной ПФ Wл(jω). Если на вход нелин-го звена дей-т гармонический сигнал: σ = asinωt (2), то первая гармоника на выходе нелин-го эл-та: ξ=B1sinωt+A1cosωt (3), где B1, A1 опред-ся как коэф-ты ряда Фурье:

Обозначив B1/a=q(a) и A1/a=q’(a), перепишем (3) в виде ξ=q(a)asinωt+q’(a)acosωt (6). Учитывая, что asinωt=σ; acosωt=ρ/ω*σ, получим:

ξ =φ(σ)=[q(a)+q’(a) ρ/ω]σ (7)- гармоническая линеаризация, коэф-ты q(a); q’(a)-коэф-ты гарм-ой линеаризации. На основании (7) нах-м ПФ линеариз-го нелин-го эл-та:

Wн(a,p)=q(a)+q’(a) ρ/ω (8) и АФХ Wн(a)=q(a)+jq’(a) (9)

Используя подстановку ψ=ωt и формулы для выч-я B1 и A1:

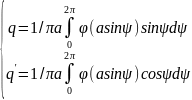(10)

На основании (10) рассчит-т коэф-ты нелинейностей. Если нечетно-симметричная нелинейность однозначна, то:

q’=0, а φ(σ)=q(a)σ (11)

С труктурная сх. линеаризованной сис-мы:

По Найквисту: Wл(j𝛚)=-1/Wн(a)