27. Акр для лин-х непрер-х систем.

Пусть возмущенное движение объекта записывается в форме

, (6.58)

где вектор перем-х состояния объекта равен разности их между фактич-ми значениями и желаемыми базовыми значениями А и В; заданные матрицы чисел размеров n  n, n  m соответственно. Необходимо найти U, которое минимизирует функционал

, (6.59)

где D и C  весовые матрицы коэффициентов.

В качестве функции  примем ква дратичную функцию , где k  положительно определенная симметричная матрица. Воспользуемся уравнением оптимальности Беллмана

. (6.60)

Подставляя производные от  в уравнение Беллмана

,

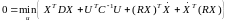а затем в уравнение динамики объекта управления, получим

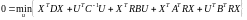. (6.61)

Экстремальное значение выражения в фигурных скобках равно

. (6.62)

Откуда имеем оптимальный закон управления

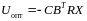(6.63)

в форме пропорц-го многомерного рег-ра. Закон оптим-го упр-ния включает матрицу, относ-но которой было принято св-во полож-сти. Для нахождения численных значений эл-тов матрицы К подставим оптим- закон управления в уравнение Беллмана.

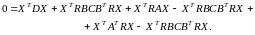
Откуда находим нелинейное матричное уравнение

. (6.64)

Среди корней этого уравнения необходимо сохранить для искомой матрицы лишь те корни, которые удовлетворяют условию положительности матрицы R.

Пример 6.1. Пусть объект управления имеет вид

a функционал качества равен

.

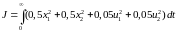Используя полученные уравнения оптимального закона управления, имеем

;

.

Коэф-ты матрицы R удовлетворяют следующим уравнениям

;

;

.

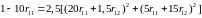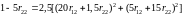Решая приведенную систему уравнений, находим

.

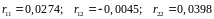Закон управления принимает окончательный вид:

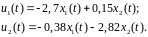
28. Акр для лин-х дискр-х систем.

Ур-ния динамики дв-я объекта упр-я в перем-х сост-я имеют вид

(6.102)

Пусть переменные удовл-т естественным граничным условиям

при функционале качества

. (6.103)

Обозначим функцию, соответствующую , через

. (6.104)

Запишем функциональное уравнение Беллмана

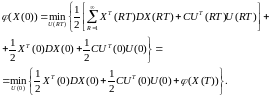(6.105)

Разложим в ряд Тейлора, сохранив в нем след-е члены

где .

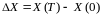С учетом принятой функции

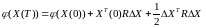(6.106)

перепишем функциональное уравнение

(6.107)

С учетом модели динамики движения объекта функциональное уравнение имеет вид

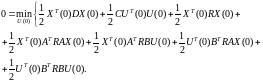(6.108)

Производная от фигурных скобок по :

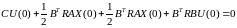; (6.109)

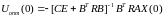. (6.110)

Обозначим выражение

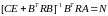, (6.111)

тогда 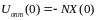(6.112)

Подставим выражение для оптимального закона в функциональное уравнение (6.105):

(6.113)

Откуда имеем уравнение для нахождения матрицы :

. (6.114)

В сравни с формми для расчета матрицы для непрерх систем полученное выражение является более сложным. Полученный закон управления справедлив для любого такта .

Пример 6.3. Пусть уравнение объекта имеет вид

,

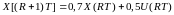а критерий качества равен

.

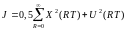В соответствии с выражением (6.107) имеем

или

Имеем .

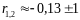Устойчивому решению будет соответствовать 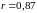. Подставляя это значение в уравнение (6.112), имеем

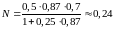
и

.

29. Синтез наблюдателей перм-х состояний.

Рассм-м ОУ, возмущенное дв-е которого опис-ся уравнением

, (6.319)

и одним из методов определен оптимальный закон управления

. (6.320)

Доступными измерению являются выходные переменные системы, связанные с переменными состояния соотношением

. (6.321)

В связи с этим возникает задача набл-я (восстановления, оценки) вектора x(t) по результатам измерения y(t) на интервале [t0, t].

Обозначим вектор перем-х сост-я, получ-х с помощью какого-либо алгоритма наблюдения через . Рассмотрим некоторые алгоритмы наблюдателей переменных состояния.

Наблюдатель полного порядка

Пусть простейший наблюдатель имеет модель

. (6.322)

Если доп-ть ур-ние (6.322) сост-щей, сод-щей измер-мый вектор Y, то такой алгоритм наблюд-я можно записать в общем, виде:

. (6.324)

Ур-ния для опр-ния матриц F, H, G м.б. получены разными способами. В простейшем случае пусть система имеет один вход и один выход. Для данного случая можно воспользоваться методом передаточной функции

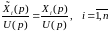. (6.325)

Преобразование Лапласа уравнений (6.319) при нулевых начальных условиях имеет вид

,

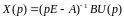где (рЕ  А)-1В есть матричная передаточная функция.

Уравнение наблюдателя (6.324), преобразованное по Лапласу при нулевых начальных условиях имеет вид

или 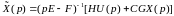. (6.326)

Подставляя в уравнение (6.326) уравнение (6.325), получим

. (6.327)

Из условия (6.325) можно записать, что

. (6.328)

Уравнение (6.328) можно трансформировать к виду

Или .

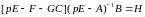Если выбрать и 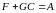, (6.329) то рав-во б-т вып-ся.

На основании (6.324) и (6.329) представим уравнения наблюдателя состояния в виде

. (6.330)

Для опр-ния матрицы G восп-ся уравнением модели ошибки

(6.331)

Или 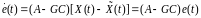. (6.332)

Уравнение (14) показывает, что ошибка оценки состояния имеет ту же самую динамику, что и наблюдатель состояния, исходя их характеристического уравнения (12):

. (6.333)

Матрицу G обычно выбирают так, чтобы ПП в наблюдателей закончился быстрее, чем ПП в системе. Эмпирически установлено, что наблюдатель должен обладать быстродействием в 2-4 раза превышающим быстродействие системы.

Обычно некот-е из переем-х сост-я доступны для измер-я и скорее всего непоср-ное измер-е перем-й будет более точным, нежели оценка перем-й с пом-ю набл-ля. Тогда разм-сть вектора сост-й набл-ля будет меньше на число измер-х корд-т (r) и такой набл-ль наз-ся редуцированным наблюдателем. Он описывается уравнениями

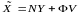;(6.344) (6.345)

где V  вектор состояний пониженного порядка (n – r). Матрицы N и  определяются из уравнения: 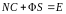. (6.346)

Необходимость этого равенства следует непосредственно из (6.344), если подставить (6.321), (6.341а). Матрица S нах-ся из уравнения: ,(6.347)

где L – произвольная матрица размера (n  r)  r.

Достаточно распространенный случай в практике Y X1