
- •Спектральная плотность стационарных процессов
- •5. Типовые статич-е нелин-сти и их х-ки.
- •7. Критерий уст-сти непрер-х лин-х систем.
- •8. Критерий уст-сти нелинейных систем.
- •9. Критерий уст-сти нелин-х систем.
- •10. Постр-е пп-сов для лин-х дискрет-х систем.
- •3) Операторный способ
- •12. Критерии кач-ва рег-ния.
- •13. Синтез системы рег-ния м-дом расчета пар-в рег-ра на желаемую степень затух-я пп.
- •14. Синтез системы рег-ния м-дом расчета пар-в рег-ра на желаемый показ-ль колебат-сти.
- •15. Синтез системы упр-я с исп-м упредителей типа Смита.
- •16. Синтез инвариантных системм упр-ния.
- •17. Многосвязные лин-е системы и их анализ.
- •18. Синтез многосв-х лин-х систем с исп-м модального упр-я и компенсаторов.
- •21. Синтез дискрет-х компенс-х рег-ров из усл-я обеспеч-я желаемого времени рег-ния.
- •22. Синтез дисктр-х компенсац-х рег-ров из усл-я, обеспеч-щих желаемое располож-е полюсов хау.
- •23. Синтез дискр-х компенс-х рег-ров из усл-я, обеспечив-щах минимизацию дисперсии вых-го сигнала лин-й системы.
- •Вариационное исчисление в оптимальном управлении
- •25. Вывод основ-х соотн-й пр-па максимума. Проблемы его исп-ния.
- •27. Акр для лин-х непрер-х систем.
- •28. Акр для лин-х дискр-х систем.
- •29. Синтез наблюдателей перм-х состояний.
- •30. Адаптив-е системы упр-я. Классифик-я. Синтез адапт-й системы с эталонной моделью на основе подстройки коэф-в ур-ния переем-х состояний.
- •Системы с адаптивной оценкой параметров
- •Адаптивное упр-ние с эталонной моделью в перем-х сост-я
- •Адаптив-ый р-тор, обеспечив-й настройку коэф-тов уравнения состояния
1. МАТ-Е ОПИСАНИЕ СИГНАЛОВ В НЕПРЕР-Х ЛИН-Х ДЕТЕРМИНИР-Х СИСТЕМАХ.
Сигнал – носитель инф-и на матер-й основе. Быв-т детермин-е и случ-е. Детерм-е: для каждого м-нта вр м предсказать знач-е. Непрер-е: аргумент сигнала чаще всего тек-е время, м зафиксир-ть бесконеч-е мн-во точек.
При анализе прохожд-я слож-го сигнала U(t) ч/з такие системы его предст-т в виде взвеш-й суммы базисных ф-ций φk(t) (или соотв-щего интеграла)
 ,
tt,
t,
где Сk
– коэф-ты; t,
t
– инт-л сущ-ния сигн-а. На инт-ле t,
t
выр-е справ-во как для сиг-в, неогр-х во
вр, так и для сигн-в конечной длит-сти.
,
tt,
t,
где Сk
– коэф-ты; t,
t
– инт-л сущ-ния сигн-а. На инт-ле t,
t
выр-е справ-во как для сиг-в, неогр-х во
вр, так и для сигн-в конечной длит-сти.
Вычисл-е
составл-щих сигнала сущ-но облегчается
при выборе в кач-ве базиса системы ф-ций
0(t),
1(t),…,
k(t),…,
j(t),…,
n,
кот-ю наз-т ортогон-й
на отрезке t,
t
для всех
 ,
если удовлетворяются условия
,
если удовлетворяются условия
 при
k
j,
(1.2) и ортонормир-й, если
при
k
j,
(1.2) и ортонормир-й, если
 при
k
=
j.
(3)
при
k
=
j.
(3)
Распр-ной вр-ной формой предст-ния сигнала явл-ся такое разлож-е сигнала U(t), при кот в кач-ве базисной ф-ции исп-тся единичные импул-е функции – дельта-ф-ции.
Мат/описание такой ф-ции зад-ся соотношениями, когда дельта-функция отличается от нуля в момент времени t = , имеем:
 (4) Для более общего случая, когда
дельта-f-я
отлич-ся от 0 в м-нт вр кси:
(4) Для более общего случая, когда
дельта-f-я
отлич-ся от 0 в м-нт вр кси:
 (5)
(5)
Такая М/М соотв-т импульсу беск-но малой длит-сти и безгр-й в-ны. С пом-ю -ф-ции можно выразить значение реального сигнала U(t) в конкретный момент времени :
 .
(6) Это рав-во справ-во для любого
тек-го м-нта вр t.
Заменив
на t
и приняв в кач-ве перем-й интегр-я
.
(6) Это рав-во справ-во для любого
тек-го м-нта вр t.
Заменив
на t
и приняв в кач-ве перем-й интегр-я
 .
(7) Ф-ция U(t)
выражена в виде сов-сти примык-щих друг
к дургу импульсов беск-но малой длит-сти.
Т.к. они не перекрыв-ся во времени, то –
ортогон-сть сов-сти этих импульсов. Ф-ла
справ-ва и для бо-лее узкого диап-на
пределов интегр-я. Так, для любого
> 0
.
(7) Ф-ция U(t)
выражена в виде сов-сти примык-щих друг
к дургу импульсов беск-но малой длит-сти.
Т.к. они не перекрыв-ся во времени, то –
ортогон-сть сов-сти этих импульсов. Ф-ла
справ-ва и для бо-лее узкого диап-на
пределов интегр-я. Так, для любого
> 0
 .
(8)
.
(8)
На практике еще исп-т производные импульсной -функции. При условии, что U(t) имеет непрерывные производные до n-го порядка, с учетом производных -функции имеем
 (9)
и аналогично
(9)
и аналогично
 (10)
(10)
при k = 1, 2,…, n.
Единич-ю импул-ю -ф-цию м предс-ть прямоуг-м импульсом конеч-й длит-сти Δ, им-щим един-ю площадь.
 (11)
Предст-м
единич-й прямоуг-й импульс интегралом
Фурье.
(11)
Предст-м
единич-й прямоуг-й импульс интегралом
Фурье.
 (12). Подст-я в (12) выр-е (11) прямоу-го
импульса:
(12). Подст-я в (12) выр-е (11) прямоу-го
импульса:

 (13)
(13)
Выполнив обратное преобразование Фурье для (13), получим
 .
(14)
.
(14)
Переходя
к пределу при Δ→0 и принимая во внимание,
что при этом
 ,
получим
,
получим
 .
(15)
.
(15)
Эта формула дает разложение мгновенного единичного импульса на гармонические колебания всех возможных частот.
Исп-е
экспоненц-х базисных ф-ций в преобр-и
Фурье комплек-сно-сопряж-ми парами (с
положит-м и отриц-м пар-м )
позв-т в соотв-и с формулой Эйлера
 (16)
(16)
представить сложный детерминир-й сигнал в виде суммы гарм-х составляющих. Поскольку параметр в этом случае имеет смысл круговой частоты, результат такого преобразования называют частотной формой представления сигнала.
2. МАТ-Е ОПИСАНИЕ СИГНАЛОВ В НЕПРЕР-Х ЛИН-Х СТОХАСТИЧ-Х СИСТЕМАХ.
Сигнал – носитель инф-и на матер-й основе. Быв-т детермин-е и случ-е. Случ-е: врем-е сигналы м охаракт-ть вероят-ми оценками. Если м извлечь полезную инф-ю – случ-й, иначе – помеха. Непрер-е: аргумент сигнала чаще всего тек-е время, м зафиксир-ть бесконеч-е мн-во точек.
Под случ-м (стохаст-м) проц-м подраз-т такую ф-цию времени U(t), знач-я кот-й в каждый м-нт времени случайны. М.б. опр-ны лишь статистич-е данные, хар-щие все мн-во возм-х реализаций.
Для этого надо превратить СП в набор случ-х чисел с опр-м шагом. СП U(t) м.б. описан сист-й N обычно зав-х случ-х в-н U1=U(t1),…, Ui=U(ti),…, UN=U(tN), взятых в разл-е м-ты времени.
Для оценки степени статистич-й зав-сти мгнов-х знач-й проц U(t) в произв-е м-нты времени t1 и t2 исп-ся неслуч-я ф-ция аргум-в RU(t1, t2), кот-я наз-ся кор-ной ф-цией. При конкр-х аргум-х t1 и t2 она = кор-му м-нту знач-й процесса U(t1) и U(t2):
 .
(17). Ч/з двумерную плотность вер-сти
выр-е (17) представляется в виде:
.
(17). Ч/з двумерную плотность вер-сти
выр-е (17) представляется в виде:
 (18), где ро – плот-сть вер-сти случ-х в-н.
Как вероятностные х-ки, так и кор-е знач-я
для опр-х м-нтов вр м.б. однор-ми набол-м
инт-ле набл-й СП (стац) и неоднор-ми (СП,
у кот-х изм-ся х-ки – нестац-е).
(18), где ро – плот-сть вер-сти случ-х в-н.
Как вероятностные х-ки, так и кор-е знач-я
для опр-х м-нтов вр м.б. однор-ми набол-м
инт-ле набл-й СП (стац) и неоднор-ми (СП,
у кот-х изм-ся х-ки – нестац-е).
В силу сим-сти этой ф-лы относ-но аргументов справ-во рав-во
 .
(19)
.
(19)
Для стацх эргодических процессов справедливы соотношения:
для
мат-го ожидания сигнала U(t):
 ;
(20)
;
(20)
для
дисперсии сигнала
 ;
(21)
;
(21)
для корреляционной функции сигнала:
 . (22),
где тау – времен-й инт-л, кот опр-т сдвиг
по вр 2х случ-х в-н, целое число.
. (22),
где тау – времен-й инт-л, кот опр-т сдвиг
по вр 2х случ-х в-н, целое число.
Дисперсия
сигнала U(t)
= кор-ной функции при
= 0:
 .
.
Спектральная плотность стационарных процессов
 .
(30)
.
(30)
Выр-е (30) – ф-ла Релея, кот-я соотв-т энерг-й форме интеграла Фурье. Для нахожд-я энергии рассм-го процесса вместо бескон-го интервала набл-я с равным основ-м можно интегр-ть квадрат ф-ции времени по всему интервалу [∞, ∞] или инт-ть квадрат модуля изобр-я Фурье по всем частотам [∞, ∞]. Для бол-ва проц-в энергия за беск-й инт-л стремится к беск-сти, что неудобно в тех-х прилож-х. Поэтому удобнее вместо энергии исп-ть ср-ю мощность процесса, кот-я будет получена, если энергию поделить на инт-л наблюд-я, тогда на осн-и формулы (30):
 .
(31)
.
(31)
Введем
обозначение
 ,
(32)
,
(32)
которое получило название спектральной плотности.
С учетом (32) перепишем выражение (31)
 ,
(33)
,
(33)
где ū2 – средний квадрат рассматриваемой величины u(t).
Важным свойством спектральной плотности является то, что интегрирование ее по частотам [∞, ∞] дает средний квадрат исходной функции времени u(t). По своему физическому смыслу спектральная плотность есть величина, которая пропорциональна средней мощности процесса в интервале частот от ω до ω + dω.
Спектральная плотность и корреляционная функция случайных процессов представляют собой взаимные преобразования Фурье:
 ;
(34)
;
(34)
 .
(35)
.
(35)
3. МАТ-Е ОПИСАНИЕ СИГН-В В ЛИН-Х ДИСКР-Х СИСТ.
Дискр (на инт-ле набл-й конечное кол-во точек отсчета аргум-та, то м/д сосед-ми точками отсчета – разрыв аргум-нта, т.е. такие же разрывы будут и для знач-й сигнала).
Из
анализа спектров сигн-в м заключить,
что наим-шая частота квант-я для возм-сти
восст-я
сигнала равна
 ,
где
,
где
 –
наивысшая частота, содерж-ся
в спектре
–
наивысшая частота, содерж-ся
в спектре
 (импул-я теорема).
Теорема утв-т, что если сигнал не сод-т
частот выше, чем
(импул-я теорема).
Теорема утв-т, что если сигнал не сод-т
частот выше, чем
 ра-диан в секунду, он полностью опис-ся
своими знач-ми, измер-ми
в дискр-е моменты времени с интервалом
ра-диан в секунду, он полностью опис-ся
своими знач-ми, измер-ми
в дискр-е моменты времени с интервалом
 секунд.
секунд.
В соотв-и с импульсной теоремой непрерывный сигнал может быть получен из дискретного по интерполяционной формуле

Преобразование
Фурье:

По
усл-ю теоремы ф-ция F
= нулю вне интервала
 .
Если
.
Если
 ,
то
,
то

 .
.
Значение
непрерывной функции на основе
 равно
равно

Меняя порядок интегрирования и суммирования, получаем

На выбор частоты квант-я влияют треб-я уст-сти замкнутых систем и др-е практ-е сообр-я, кот-е могут сделать необх-м квант-е сигнала с частотой более высокой, чем теор-й минимум. Более того, сигналы с огранич-м спектром физически не сущ-т в системах связи или упр-я. Все физ-е сигналы, сущ-щие в реальном мире, содержат гармоники, покрывающие широкий диапазон частот. Но вследствие того, что амплитуды высокочастот-х сост-щих значит-но ослаблены, предпол-ся, что сигнал имеет огранич-й спектр. Поэтому на практике эти факторы в сочетании с нереализ-ю ид-го низкочаст-го фильтра делают невозм-м точное воспроизвед-е непрер-го сигнала по его дискретным выборкам, даже если выполняются условия импульсной теоремы.
Также
сигнал м.б. полностью опр-н при квант-и
его со скор-ю меньшей, чем
радиан в секунду, если в м-нты выборки
известна инф-я, как об амплитуде сигнала,
так и о его производных. Если сигнал не
содержит частот больших, чем
радиан в секунду, он полностью определяется
значениями
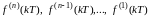 и
и
 ,
измер-ми в дискр-е м-нты времени с инт-лом
,
измер-ми в дискр-е м-нты времени с инт-лом
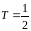
 секунд, где
секунд, где
 (53)
(53)
Это
означает, что если кроме значений
 в м-нты
в м-нты
 известны знач-я первой производной
известны знач-я первой производной
 ,
то макс-но доп-й период квантования
,
то макс-но доп-й период квантования
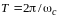 .
Это вдвое больше периода, необх-го при
измерении только
.
Это вдвое больше периода, необх-го при
измерении только
 .
Добавление каждой последующей производной
позволяет ув-ть интервал между выборками
до величины
.
Добавление каждой последующей производной
позволяет ув-ть интервал между выборками
до величины

 ,
где n
–
порядок высшей производной, при условии,
что для каждой выборки все производные
низших порядков известны.
,
где n
–
порядок высшей производной, при условии,
что для каждой выборки все производные
низших порядков известны.
