20. Определение производной, её геометрический и механический

смысл. Производной функции y=f(x) в точке х нулевое,называется предел отношения приращения функции к приращению аргумента,когда приращение аргумента стремится к нулю.

Если существует конечный предел 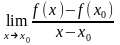, то он называется производной функции

f в точке х₀.

Обозначение: .

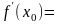Разность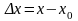 называется приращением аргумента, а 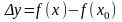- приращением функции. Таким образом, можно определить производную как .

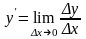Геометрический смысл: значение производной при данном значении х равно тангенсу угла, образованного касательной к графику функции в точке с соответствующим значением х с положительным направлением оси Ох.

Механический смысл производной.Рассмотрим прямолинейное движение тела, для которого пройденное расстояние есть функция от времени: s=f(t). Среднюю скорость за время Δt можно определить по формуле:

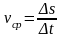. Для определения мгновенной скорости тела в данный момент времени устремим Δt к нулю. Получим: 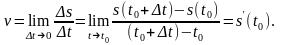Таким образом, производная от расстояния в данный момент времени равна мгновенной скорости движения в этот момент. Соответственно производная любой функции при данном значении аргумента равна скорости изменения этой функции при рассматриваемом х.

21. Производная суммы, произведения и частного. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

Производная произведения функций.Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и

Производная произведения двух функций не равана произведению производных этих функций.

Производная частного функций. Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле

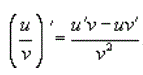
22. Дифференциал функции, его геометрический смысл. Непрерывность

дифференцируемой функции. Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)): dy=ƒ'(х)•∆х.

Функция f(x),называется дифференцируемой в точке х₀ , если в ее приращ ении Δу можно выделить линейную часть,т.е. если Δу можно представить в виде Δу=А* Δх+α* Δх,где А=const,а α= α(х)-б.м. в точке х0.

Диффиренциал функции y=f(x) вычисляется по формуле: dy=f’(x)dx,где dx-дифференциал переменной х.

Геометрический смысл:дифференциал функции равен приращению ординаты касательной. Выясним геометрический смысл дифференциала.

Для этого проведем к графику функции у=ƒ(х) в точке М(х; у) касательную МТ и рассмотрим ординату этой касательной для точки х+∆х (см. рис. 138). На рисунке ½ АМ½ =∆х, |AM1|=∆у. Из прямоугольного треугольника МАВ имеем:

Но, согласно геометрическому смыслу производной, tga=ƒ'(х). Поэтому АВ=ƒ'(х)•∆х.

Сравнивая полученный результат с формулой (24.1), получаем dy=АВ, т. е. дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.

В этом и состоит геометрический смысл дифференциала.

Непрерывность дифференцируемой функции

Теорема 1. Пусть функция y = f(x) дифференцируема на интервале (a, b). Тогда функция f непрерывна на (a, b).

Доказательство: Возьмем произвольное фиксированное число x (a,b).

По условию теоремы

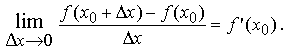
Следовательно, в малой окрестности числа x0 можно определить функцию α = α(Δx), стремящуюся к нулю при ∆х->0 такую, что

Но тогда

и, следовательно, функция f непрерывна при x = x0. Так как число x0 – произвольное, то функция f непрерывна на всем интервале (a, b).Теорема доказана.

Из доказанной теоремы непосредственно вытекает, что в точках разрыва функция не может быть дифференцируемой.