Билет 1

1.Понятие случайного события. Явления, рассматриваемые с т. зр., осуществились они или не осущ-лись, наз. событиями. К событиям ставится осн-я задача: предсказать, появится ли изуч-ое событие при осущ-нии некот-го наперед заданного комплекса фак-ров (явлений — причин). Событие, кот. при заданном комплексе фак-ров обяз-но произойдет наз. достоверным, а то, кот. не может произойти, наз. невозможным событием. Суждения о достоверн. или невозмож-ти некот-го события явл. категорическими суждениями, их принято, считать окончат-ым рез-том исслед-я. Событие, кот. при заданном комплексе фак-ров может либо произойти, либо не произойти, наз. случайным событием. Случайные события связ. с действием не вошедших в организованный комплекс фак-ров, наз-мых случайными фак-рами в отличие от др. гр. фак-ров, вкл-мых в комплекс и наз. основными, или неслучайными. Предсказать рез-тат 1ного испытания можно т! д/достоверных или невозможных событий. Случайность же события не видна из 1ного испытания. Теория оценки случайных событий строится на большом числе испытаний. Важн. условием при этом явл. неизменность комплекса основных фак-ров. События, происх-ие при одном и том же комплексе фак-ров, наз. однородными. Однородные случайные события в большой их массе подчин-ся некот. вероятностным зак-тям. (Н: подбросить монетку 50% орел, 50% решка)

2. Кластерный анализ объед-ет различ/ процедуры, д/классиф-ии, в рез-те их примен-я исходная совокуп-ть объектов разделяется на кластеры или гр. (классы) схожих м/у собой объектов. Кластер – гр. объектов, облад-их св-вом плотности (плотность объектов внутри кластера выше, чем вне его), дисперсией, отделимостью от др. кластеров, р-ром.

Сложность задач кластерного ан-за состоит в том, что реальные объекты явл-ся многомерными, то/е опис-ся не 1ним, а неск-кими парам-ми, и объединение объектов в гр. проводится в пространстве многих измерений. Кроме того, данные могут носить нечисловой хар-ер. Методы кластеризации делятся на: 1)агломеративные (объединительные) - происх.т последовательное объед-е наи>ее близких объектов в 1н кластер, график в виде дерева объединения. 2) итеративные дивизивные (разделительные). Чаще реализ-ся агломеративные методы кластеризации.

Кластерный ан-з – это совокуп-ть методов классификации многомерных наблюдений или объектов, основанных на опред-ии понятия расстояния м/у объектами с последующим выделением из них гр., "сгустков" наблюдений (кластеров, таксонов). Выбор конкретного метода кластерного ан-за зависит от цели классиф-ции. Обычно п/д началом классиф-ции данные стандартизуются (вычитается среднее и производится деление на корень квадратный из дисперсии). Получ-ые в рез-те стандартизации переменные им. нулевое среднее и единичную дисперсию. Правила иерархического объед-я кластеров: -метод одиночной связи (объед-ся 2 объекта, им. м/у собой max меру сходства к ним присоед-ся объект с max мерой сходства с 1ним из объектов кластера…и т.д. Т. о. д/вкл-я объекта в кластер требуется max сходство лишь с 1ним членом кластера.); -метод полной связи (мера сходства м/у объектом – кандидатом на вкл-е в кластер и всеми членами кластера не м/б < порогового значения); -метод «средней связи» (мера сходства м/у кандидатом и членами кластера усредняется); -метод Уорда (проводить объед-е, дающее min приращение внутригр-вой суммы квадратов отклонений); -итеративный метод k-средних (метод раб. непосред-но с объектами, а не с матрицей сходства; объект относ-ся к тому классу, евклидово расстояние до кот. min; объекты рассм-ся как т. евклидова простр-ва).

Билет 2

1. Вероятность случайного события. Числовая хар-ка случайного события, облад-я тем св-вом, что д/любой достаточно большой серии испытаний частота события лишь незначит-но отлич-ся от этой хар-ки, наз. вероятностью события. Вероятность - тот теоретич. предел, к кот. стремится частота событий при увеличении числа испытаний. Вероятность (статистич-ое опред-е)– идеальное выражение частоты событий. Сущ-ют также геометрическое (Пригодно не т! д/плоскости, но и д/прямой или пространства. В 1ом случае основой д/определения вероятности служит некот. отрезок, а случайным событиям соответствуют его части. Вероятность вычисляется как отнош-е длины частей к общей длине отрезка. Во 2ом, случае основой к испытанию приним. некоторый куб, случайным событиям соответствуют различные тела, расп-ные в кубе. Вероятность вычисляют как отношение объемов тел к объему куба) и классическое (Вероятность здесь определяется априори, до испытаний, исходя из опред-ой струк-ры случайных событий, т. е. из разбивки на равновозможные исходы (подбрасывание монетки). Классич. вероятностью случайного события наз. отнош-е числа исходов, благоприятствующих событию, к числу всех возможных исходов) опред-я вероятности.

2. Дискриминантный анализ (ДА). Цель ДА: на основе измерения различных хар-тик (признаков, параметров) объекта классифицировать его, то есть отнести к 1ной из неск-их групп некоторым оптимальным способом (либо min матем-го ожидания потерь, либо min вероятности ложной классиф-ии). ДА – многомерный вид ан-за, т.к. измеряется неск-ко парам-ров объекта (Н: t, влажность, давление, состав крови, t больного и т.д). Oбл. применения ДА – биолог., мед., управление производством, эконом., геолог., контроль качества. В мед. объект исслед-я - пациент, когда по рез-татам измерений различ. парам-ров, проведения диагностических тестов врач опред-ет, необходимо ли хирургич-ое вмешательство при лечении.

В ДА можно задать априорные вероятности принадлежности объекта к опред-му классу. На практике эти вероятности оцениваются из массива эксперимент-ых данных. Д/практич-их целей реализовано 2 общих метода ДА: стандартный и пошаговый (включения и исключения). В случае 2 гр методом наименьших квадратов строится регрессионная прямая (зависим. переменная – № группы, все ост-е переменные – независ.). Если групп неск-ко, то можно представить себе, что вначале строится дискриминация между гр. 1 и 2, затем между 2 и 3, и т.д.

В пошаговом методе модель строится послед-но по шагам. Д/метода включения на каждом шаге оценивает вклад в функцию дискриминации не включенных в модель переменных. Переменная, дающая наи>ий вклад, включается в модель следующ. шаг. Если применяется пошаговый метод исключения, то вначале в модель вкл-ся все переменные  производится их последовательное исключение.

Билет 3

1. Основные теоремы теории вероятностей. Если некоторое событие может произойти при n испытаниях и а – число исходов, кот. благоприятствуют наступлению события, а b – не благоприятствуют, то вероятность того, что событие произойдет р = а/n, a того, что не произойдет: q = b/n. Сумма благоприятствующих (а) и неблагоприятствующих (b)случаев = числу всех случаев (а+b = n). Разделив все члены этого равенства на n получим: а/n + b/n = 1 или p +q = 1, т. е. сумма вероятностей 2 несовместных событий =1. Сложение вероятностей: eсли в урне с 10 шарами 6 шаров черных, 3 белых и 1 зеленый, вероятности этих событий = 6/10, 3/10 и 1/10.Какова вероятность вынуть белый или зеленый шар? p = 3/10 + 1/10 = 4/10 = 0,25, т. е. вероятность суммы 2 несовместных (взаимоисключающих случайных) событий = сумме их вероятностей. Умножение вероятностей: 2 события наз-ся независ., когда наступление 1го не оказывает влияния на наступление др-го. Вероятность наступления 2 событий независ. др. от др. = произведению вероятностей отдельных событий. (Н: вероятность выпад-я 1, а затем 2, при 2ух послед-ных бросаниях кубиков, равна р = 1/6*1/6 = 1/36). Вычисление вероятностей: требуется определить вероятность выпадения 5 очков при одновр. бросании 2 кубиков. Вероятность получения 1 на кубике а = 1/6 и получения 4 на кубике b – также 1/6. Вероятность получения комбинации этих очков = 1/36. Аналогично и вероятность 3х др. комбинаций = 1/36. Любой из этих 4х рез-тов, дающий в сумме 5 очков, будет считаться благоприятным исходом. Отсюда вероятность искомого исхода: р = 1/36 + 1/36 + 1/36 + 1/36 = 1/9.

2. Дисперсионный анализ (ДА) с классификацией по 2м признакам. ДА применим и при классификации по нескольким признакам. В 2хфакторном опыте, поставленном методом обычных повторений, сумма квадратов д/вариантов C_V расчленяется на 3. ( С_Y – общая сумма квадратов; взаимодействие внури (C_Z) и м/у выборками (C_V)): C_V = (С_А + С_В + С_АB) + С_Z;

Дисперсионный 2хфакторный ан-з по изучению градаций ф-ра А (число вар-тов l_A) и градаций ф-ра В (число вар-тов l_B), проведенного в n повторностях, осущ-ся по этапам: 1)Опред-ся суммы и средние по вар-там, общая сумма и средняя по опыту. 2)Вычисляются общая сумма квадратов отклонений, сумма квадратов д/вариантов и остатка:

N = l_Al_B n;

;

;

;

.

Д/вычисления сумм квадратов по ф-рам А, В и взаимод-ю АВ составляется вспомогательная таблица, в кот. запис-ся суммы по вар-там. Суммируя цифры, нах-ся суммы А, суммы В и вычисляются суммы квадратов отклонений д/главных эффектов и взаимод-я.

Сумма квадратов д/ф-раА: при (l_А – 1) степенях свободы.

Сумма квадратов д/ф-ра В:

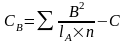при (l_В – 1) степенях свободы.

Сумма квадратов д/взаимод-я АВ нах-ся по разности: 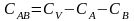при (l_А – 1)(l_В – 1) степенях свободы. Суммы квадратов запис. в табл. ДА и опред-ют фактические знач-я критерия F (F_f≥F_s – нулевая гипотеза отверг-ся и приним. альтернативная, кот. подтвержд. достоверн. отличия )

Билет 4.

1. Биномиальное разложение и измерение вероятностей. Вероятность наступления некот-го случайного события А при единичном испытании равно р. Производится серия испыт. в каждом из кот. случайное событие А может наступить с этой вероятностью р, испытания независ. др. от др. Если подбрас-ся одновр. 2 монеты (а, b), то сущ-ют 4 возможных случая выпадения гербаТ и цифры Н: ТТ, 2ТН, НН. Из 2х событий имеем:(р +q)² = p² + 2pq + q². , При p =q= 1/2  p²= q² = 1/4, а 2 рq = 1/2 получим (1/2 + 1/2)² = 1/4+1/2+1/4.

Если 3 монеты а, b, с подбрасываются одновременно, получим 8 возможных комбинаций

(р + q)³ = p³ + 3p²q + 3pq² + q³; (1/2 + 1/2)³ = 1/8 + 3/8 + 3/8 + 1/8.

Если желаем получить вероятные численности разных исходов при данном числе испытаний n, применяем выражение:

N*(p+q)ⁿ. Н: при числе испытаний N = 200 и 2х независ. событиях n в каждом испыт-ии вероятные численности будут: 200(p+q)² = 200(р²+2рq+q²). Если p = q = 1/2, им. последовательные вероятные численности: 50 + 100 + 50.

При подбрасывании монеты 200 раз (N = 200) выпадения герба ожидается в 50 случаях, герба или цифры – в 100 случаях и цифры – 50 случаях.

Вероятные численности появления альтернативных, дискретно варьирующих признаков м/б найдены по ф-ле бинома Ньютона:

где n – число независимых исходов в одном испытании; р – вероятность благоприятного исхода одного случая; q – вероятность неблагоприятного исхода; N – общее число испытаний (исходов).

2. Критерий F-отношение дисперсий. Заключение о равенстве сред. арифметич-го в выбрке. Нулевая гипотеза: Н₀: μ₁= μ₂= ...= μ₀ (средние групп одинаковы). Фишер предложил критерий — отнош-е дисперсий, распред-е кот-го получено на основе случайных выборок из 1ой общей совокупности. получено теоретич-ое распред-е F-критерия д/разных уровней значимости и д/различного числа степеней свободы. Если из нормально распределенной совокупности взять 2 независ-ые выборки объемом n₁ и n₂ и подсчитать дисперсии и со степенями свободы ν₁ = n –1 и ν₂ = n₂–1, то можно опред-ть отношение дисперсий:

Отношение дисперсий берут таким, чтобы в числителе была >шая дисперсия, и поэтому F ≥ 1.

Распред-е F зависит т! от числа степеней свободы ν₁ и ν₂. Когда 2 сравниваемые выборки явл-ся случайными независ-ми из общей совокупности с генеральной средней , то фактич-ое значение F не выйдет за опред-е пределы и не превысит критич-ое д/данных ν₁ и ν₂ теоретич-ое значение критерия F (F_факт < F_теор). Если генеральные парам-ры сравниваемых групп различны, то F_факт > F_теор. Теоретические значения F для 5%-ного и 1%-ного уровня значимости даны в табл.. На основании сопоставления F, полученного в опыте, с табл-ми знач-ми можно сказать, если значение F >, чем стандартное нулевая гипотеза Н₀: μ₁= μ₂= ...= μ₀ отвергается.

Билет 5