§7. Надежность системы с резервом и ремонтным органом

Рассмотрим систему, в которой имеется n соединенных последовательно (в смысле надежности) одинаковых основных элементов и скользящий ненагруженный резерв в количестве m таких же элементов. Кроме того, существует ремонтный орган, который в случае отказа основного элемента (и его замены из резерва) восстанавливает отказавший элемент. Пропускную способность ремонтного органа будем считать ограниченной таким образом, что одновременно может восстанавливаться не более r элементов. В случае большего количества элементов, требующих восстановления, часть из них образует очередь перед ремонтным органом. После восстановления элемент поступает в резерв.

Соответствующая этим условиям схема показана на рис. . Перемещения элементов между основной группой, ремонтным органом и резервом показаны стрелками (физических перемещений может и не быть).

Ремонтный орган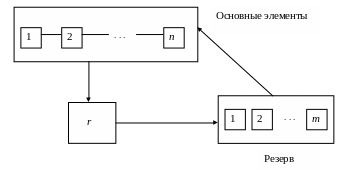

Рис.4.7.1

Отказ системы наступает в случае потери работоспособности (m+1) элемента (исчерпан резерв и отказал еще один элемент), после чего работа основной группы элементов приостанавливается, и дальнейших отказов произойти не может вплоть до восстановления ремонтным органом по крайней мере одного элемента. После этого работа системы возобновляется. При таких условиях нет необходимости восстанавливать одновременно более (m+1) элементов:

r ≤ m+1. (4.7.1 )

Таким образом, в каждый момент времени система находится в одном из (m+2) состояний, характеризуемых числом i отказавших и еще не восстановленных элементов. Число i имеет возможные значения 0, 1,2, … , m, (m+1).

Предположим далее, что время безотказной работы каждого элемента распределено по экспоненциальному закону с интенсивностью отказов λ, и такому же закону с параметром μ (интенсивность восстановления) подчинено время его восстановления. Поставим задачу расчета коэффициента готовности системы.

Введем вероятности P_i (t) (i = 0, 1, 2, …,m, (m+1)) того, что в момент t реализуется состояние с номером i, чему соответствует отказ i элементов. Составим уравнения для вероятностей, относящихся к двум близким моментам времени t и (t+Δt), подобно тому, как это было сделано в предыдущих параграфах. Предварительно рассмотрим несколько формул.

Вероятность отказа за Δt одного из основных элементов согласно формуле ( ) и с учетом их общего количества n равна

nλΔt. (4.7.2)

Вероятность противоположного события (отсутствия отказов за Δt) составляет

1 – nλΔt. (4.7.3)

Вероятность восстановления за Δt одного из нескольких отказавших элементов зависит от того, превышена или нет предельная пропускная способность ремонтного органа. Если число i отказавших элементов не превосходит r, то все они могут восстанавливаться одновременно, и эта вероятность составит

iμΔt, (i ≤ r). (4.7.4)

Если число i отказавших элементов окажется больше r, то одновременно восстанавливаться могут только r из них, и эта вероятность составит

rμΔt, (i > r). (4.7.5)

Вероятность противоположного события (за Δt восстановления не произошло) запишется соответственно в виде

1 – iμΔt, (i <r) (4.7.6)

и

1 – rμΔt, (i ≥ r). (4.7.7)

Выражения ( ) – ( ) приведены с точностью до величин о(Δt) по причинам, обсуждавшимся ранее, и последующие выкладки подтвердят отсутствие необходимости сохранения этих величин.

Для вероятности P₀ (t+Δt) имеем

P₀ (t+Δt) = P₀ (t)(1 – nλΔt) + P₁ (t)μΔt + о(Δt). (4.7.8)

Первое слагаемое правой части это вероятность нахождения системы в момент времени t в состоянии 0 и сохранения этого состояния за Δt. Второе слагаемое – вероятность нахождения системы в момент времени t в состоянии 1 и перехода за Δt в состояние 0 за счет восстановления отказавшего элемента. Третье слагаемое объединяет вероятности остальных возможных переходов в состояние 0, связанных с отказами или восстановлениями за Δt более одного элемента, а также учитывает точность, с которой записаны выражения ( ) – ( ).

Для вероятности P_i(t+Δt) состояния с некоторым номером i при 1≤ i < r получим

P_i(t+Δt) = P_i-1(t) nλΔt + P_i(t)(1 – nλΔt)( 1 – iμΔt) + P_i+1(t)(i +1)μΔt+ о(Δt),(4.7.9)

(1≤ i < r).

В отличие от уравнения ( ) в правой части ( ) появилось еще одно слагаемое, предусматривающее переход в состояние i из состояния с номером, на 1 меньшим (в случае с P₀ такого состояния просто нет). Использованы выражения ( ), ( ), ( ), ( ).

Для вероятности P_i(t+Δt) состояния с некоторым номером i при i ≥ r получим

P_i(t+Δt) = P_i-1(t) nλΔt + P_i(t)(1 – nλΔt)( 1 – rμΔt) + P_i+1(t)rμΔt+ о(Δt), (4.7.10)

(m ≥ i ≥ r).

Изменения по сравнению с ( ) обусловлены применением выражений ( ), ( ).

Для вероятности P_m+1 получим

P_m+1(t+Δt) = P_m(t) nλΔt + P_m+1(t)( 1 – rμΔt) + о(Δt). (4.7.11)

В правой части уравнения ( ), как и в ( ) всего три слагаемых, поскольку состояния с номером (m+2) не существует.

Приведем уравнение ( ) к виду

(4.7.12)

и перейдем к пределу при Δt→0

(4.7.13)

Такие же действия по отношению к ( ),( ) и ( ) приводят к следующим результатам

, (1≤ i < r). (4.7.14)

, (m ≥ i ≥ r). (4.7.15)

. (4.7.16)

Имея в виду отыскание в дальнейшем коэффициента готовности как не зависящего от времени показателя, будем искать далее не зависящее от времени, установившееся решение для уравнений ( ) – ( ). Для этого приравняем все производные 0, а в обозначениях вероятностей опустим аргумент t:

(4.7.17)

, (1≤ i < r), (4.7.18)

, (m ≥ i ≥ r), (4.7.19)

(4.7.20)

Получилась однородная система (m+1) линейных алгебраических уравнений относительно такого же количества неизвестных вероятностей. Она позволяет выразить все вероятности через одну из них, например, P_0. Непосредственной проверкой легко убедиться, что эти выражения имеют вид

< r, (4.7.21)

(4.7.22)

Для определения P_0. следует дополнительно использовать условие полноты

, (4.7.23)

Откуда после подстановки ( ), ( ) получаем

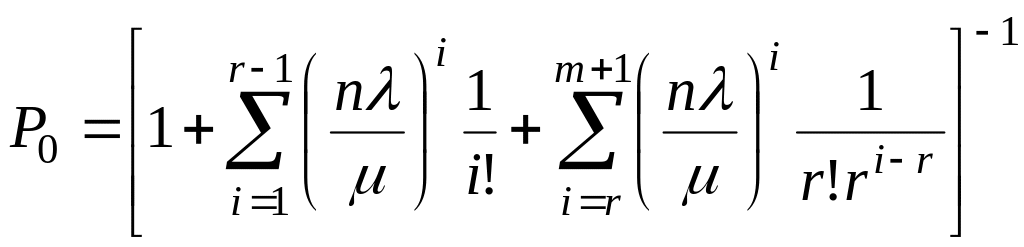. (4.7.24)

Вероятность неработоспособного состояния системы в некоторый момент времени определится по формуле

, (4.7.25)

а коэффициент готовности как вероятность противоположного события – по формуле

K_Г = 1 – P_m+1. (4.7.26)

▲Пример. В системе n=10 основных элементов, m=2 резервных, и ремонтный орган может одновременно восстанавливать r=2 элемента. Интенсивность отказов одного элемента λ= 10^-3 1/час, а среднее время его восстановления T_в = 50 час.

Находим μ = 1/T_в = 0,02 1/час, nλ/μ = 0,5. Используя формулы ( ), ( ) и ( ), получим

P₀ = [1+0,5+ (0,5)² /2! + (0,5)³ /2!2]^-1 = 0,6406 ;

P₃ = 0,6406∙(0,5)³ /2!2 = 0,01;

K_Г = 0,99.

При r=1 K_Г = 0.933.

В отсутствие резерва T_o =1/nλ=100 час. K_Г = T_o/(T_o+T_в)=100/(100+50)= 0,667.▲