• Матрица. Основные понятия.

Пусть m и n два произвольных натуральных числа. Матрицей размера m на n называется совокупность m*n вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. При этом сами числа называются элементами матрицы и каждому элементу ставится в соответствие два числа -номер строки и номер столбца.

Для обозначения матрицы используются прописные латинские буквы, при этом саму матрицу заключают в круглые или прямоугольные или в двойные прямые скобки. Элементы матрицы обозначают строчными латинскими буквами, снабжёнными двумя индексами: aij - элемент матрицы, расположенный в i-й строке и j-м столбце или коротко элемент в позиции ( i, j ). Приведём некоторые обозначения, которыми будем пользоваться в дальнейшем:

A=(aij) - матрица A с элементами aij в позиции ( i , j );

Элементы, где i=j, называются диагональными, а остальные - вне диагональными. Совокупность диагональных элементов  a1 1 a 2 2 a 3 3 , где k = min (m,n), называется главной диагональю матрицы.

Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается символом O.

Заметим, что для каждого размера m*n существует своя нулевая матрица.

Матрица размера n на n называется квадратной матрицей n-го порядка, т.е. число строк равно числу столбцов.

Квадратная матрица называется диагональной, если все ее внедиагональные элементы равны нулю.

Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной матрицей и обозначается символом I или E.

Матрица размера 1*n называется матрицей-строкой или вектор-строкой. Матрица размера 1*m называется матрицей столбцом или вектор-столбцом.

• Линейные операции над матрицами : сложение, умножение на число, произведение матриц, транспонирование, свойства операций.

Основные операции, которые производятся над матрицами, – сложение, вычитание, умножение, а также умножение матрицы на число. Указанные операции являются основными операциями алгебры матриц – теории, играющей весьма важную роль в различных разделах математики и естествознания.

Суммой двух матриц А и В одинаковых размеров называется матрица того же размера, элементы которой равны сумме соответствующих элементов матриц А и В.

Операция нахождения суммы матриц называется сложением матриц и распространяется на случай конечного числа матриц одинаковы размеров.

Операция нахождения разности двух матриц называется вычитанием матриц. Проверкой можно убедиться, что операция сложения матриц удовлетворяет следующим свойствам:

1)А + В = В + А; (коммутативность)

2)А + (В + С) = (А + В) + С; (ассоциативность)

3)А + О = А.

Здесь А, В, С – произвольные матрицы одинаковых размеров; О – нулевая матрица того же размера.

Произведением матрицы А = [аij] на число λ называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением их на число λ.

Операция нахождения произведения матрицы на число называется умножением матрицы на число. Матрица – А = –1А называется противоположной матрице А. Проверкой можно убедиться, что операция умножения матрицы на число удовлетворяет следующим свойствам:

1)1*А = А;

2)(λ + μ)* А = λ*А + μ*Α;

3)λ* (А + В) = λ*Α+ λ*В;

4) λ*(μ*А) = (λ*μ)* А;

5) А + (-А) = О.

Здесь А, В - произвольные матрицы; μ, λ – произвольные числа; О – нулевая матрица.

Произведение АВ матрицы А на матрицу В определяется только в том случае, когда число столбцов матрицы А равно числу строк матрицы В.

В этом случае произведением матрицы А на матрицу В, которые заданы в определённом порядке (А – 1-ая, В – 2-ая), является матрица С, элемент которой сij определяется по следующему правилу:

cij = a i 1 * b1j + a i 2 * b 2 j + … + a i n * b n j = ∑ n α = 1* aiα *bαj,

где i = 1,2, …, m; j = 1, 2, …, k.

Для получения элемента сij матрицы произведения С = АВ нужно элементы i-й строки матрицы А умножить на соответствующие элементы j-го столбца матрицы В и полученные произведения сложить.

Число строк матрицы С = АВ равно числу строк матрицы А, а число столбцов – числу столбцов матрицы В.

Операция нахождения произведения двух матриц называется умножением матриц.

Сравнив правые части выражений (2) и (3), убедимся, что АВ ≠ ВА.

Матрицы А и В, для которых АВ = ВА, называются перестановочными. Проверкой можно показать, что умножение матриц удовлетворяет следующим свойствам:

1)А*(В*С) = (А*В)* С; (ассоциативность)

2)λ*(А*В) = (λ*А)*В = А*(λ*В);

3)А*(В + С) = А*В + А*С. (дистрибутивность)

Здесь А, В, С – матрицы соответствующих определению умножения матриц размеров; λ – произвольное число.

Операция умножения двух прямоугольных матриц распространяется на случай, когда число столбцов в 1-ом множителе равно числу строк во 2-ом, в остальных случаях произведение не определяется. А также, если матрицы А и В - квадратные одного и того же порядка, то умножение матриц всегда выполнимо при любом порядке следования сомножителей.

• Определитель матриц 1, 2, 3-го порядка.

Определитель можно посчитать только для квадратных матриц. Определителем матрицы первого порядка будет сама матрица, так как в ней будет содержаться только один элемент. Определитель второго порядка считается по формуле: разность произведений главной и побочной диагонали. Определитель третьего порядка считается по правилу треугольника.

• Миноры и алгебраические дополнения элемента квадратной матрицы

Минором Mij  элемента cij матрицы  n-го  порядка называется определитель матрицы  (n-1)-го порядка, полученный из матрицы  А  вычёркиванием  i-й строки и  j-го столбца.

Алгебраическим дополнением  А_ij  элемента а_ij матрицы  n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца: А_ij =(-1)^(i+j)*M*А_ij, то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – чётное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечётное число. (^ - символ возведения в степень).

• Определитель квадратной матрицы. Произведение порядка.

• Свойства определителей.

1).Свойство равноправности строк и столбцов:

Определитель транспонированной матрицы равен определителю изначальной матрицы.(|Aт|=|A|)

2).Свойство антисимметрии при перестановке двух строк (или двух столбцов):

При перестановке местами двух строк (или двух столбцов) определитель сохраняет свою абсолютную величину, но меняет знак на противоположный.

• Обратная матрицы: определение, теорема о существовании, свойства.

Рассмотрим квадратную матрицу:

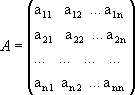
Обозначим D =det A.

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если D = 0.

Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.

Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Свойства:

• Определитель обратной матрицы равен обратной величине определителя исходной матрицы

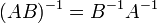• для любых обратимых матриц А и В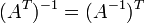

• , где Т-транспонированная матрица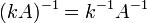

• , при любом к, не равном 0

• Ранг матрицы. Свойства ранга матрицы

Ранг матрицы - наибольший из порядков ее миноров не равных нулю. Ранг матрицы А обозначают одним из символов: rang А, r. Если все миноры матрицы равны нулю, то ранг ее считается равным нулю.

Из определения ранга матрицы получаем следующие утверждения:

• Ранг матрицы определяется целым числом, заключенным между 0 и меньшим из чисел m, n.

• Ранг матрицы равен нулю, если матрица нулевая.

• Для квадратной матрицы n-го порядка r = n тогда и только тогда, когда матрица невырожденная.

Свойства ранга:

• Ранг матрицы, полученной транспонированием, равен рангу исходной матрицы.

• Ранг матрицы останется неизменным, если вычеркнуть или приписать нулевую строку (т. е. строку, все элементы которой равны нулю) или нулевой столбец.

• Ранг матрицы.Св-ва ранга матрицы

Системой m линейных уравнений с n неизвестными называется система вида

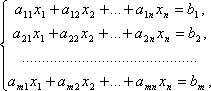
Коэффициенты при неизвестных будем записывать в виде матрицы, которую назовём матрицей системы:

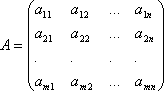
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.

• Система может иметь одно решение.

• Иметь бесконечное множество решений(записывается общее и частное решение)

• Не иметь решений.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

• Метод решения СЛУ припомощи обратной матрицы

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

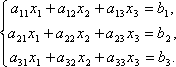
Рассмотрим матрицу системы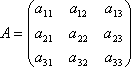 и матрицы столбцы неизвестных и свободных членов

Найдем произведение

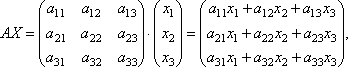
Это левая часть системы уравнений. В итоге получается

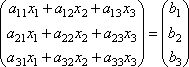
Или АХ=В, откуда Х находится, как X = A-1B.

• Метод Крамера.

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

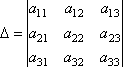
называется определителем системы.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

• Метод Гауса

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

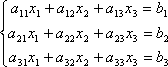
Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а21 и умножим на –а11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а31 и умножим на –а11, а затем сложим с первым. В результате исходная система примет вид:

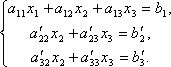
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

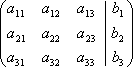
и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

перестановка строк или столбцов;

умножение строки на число, отличное от нуля;

прибавление к одной строке другие строки.

• Вектор: основные понятия.

Направленный отрезок или, что то же самое, упорядоченную пару точек будем называть вектором. Обозначается вектор одной буквой или . Векторы характеризуются длиной и направлением. Мы рассматриваем свободные векторы, т. е. такие, которые без изменения длины и направления могут быть перенесены в любую точку пространства.

Ортом вектора называется вектор , который имеет единичную длину и то же направление, что и вектор .

Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.

Векторы, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными.

Два вектора считаются равными, если они коллинеарные, одинаково направлены и равны по длине.

Пусть даны два вектора. Параллельным переносом приведем их к общему началу. Наименьший угол, на который надо повернуть один вектор до совпадения с другим, называется углом между векторами.

(Остальные определения смотрите в тетрадке вначале раздела Векторная алгебра!!!!!!!!!)

• Линейные операции над векторами: сложение, вычитание, умножение вектора на число.

Сложение векторов.

Пусть есть а^- и в^-. Возьму произвольную т. О и построю ОА=а^-. От т. А отложу АВ=в^-. Вектор ОВ, соединяющий начало первого с концом второго, есть с^-, равный а^-+в^-. Это правило треугольника. С его помощью можно найти сумму более 2-ух векторов.

А если начало а^- и начало в^- поместить в т. О, и достроить фигуру до параллелограмма, то вектор, совпадающий с диагональю ОВ, искомый. Это правило параллелограмма.

Разность векторов.

Вектор с^-, который в сумме с в^- дает а^-. Если начала а^- и в^- поместить в т. О, и фигуру достроить до параллелограмма, то вектор лежит на диагонали, исходящей из конца в^- и входящей в конец а^-. По правилу параллелограмма.

Можно использовать понятие противоположного вектора и определение суммы векторов: а^--в^-=а^-+(-в^-). Из точки О построю а^-, от т. А отложу в^-, развернутый на 180 градусов (относительно своего направления). Вектор, соединяющий начало первого с концом второго, искомый. По правилу треугольника.

Умножение вектора на число.

Призведение вектора а^- на число h – вектор hа^-, который имеет длину, равную произведения модуля h на модуль а^-: hа^-=IhI*Ia^-I=Iha^-I Вектор hа^- коллинеарен и сонаправлен а^-, если h>0; и противоположен, если h<0.

Свойства линейных операций. Позволяют преобразовывать вектора как в обычной алгебре.

1. а^-+в^-=в^-+ а^- коммутативность сложения

2. а^-+(в^-+с^-)=(а^-+в^-)+с^- ассоциативность сложения

3. h₁*(h₂*a^-)= h₁*h₂*a^-

4. h₁*(a^-+b^-)=h₁*a^-+h₂*b^-

5. (h₁+h₂)*a^-=h₁*a^-+h₂*a^-

15/16. Проекция вектора на ось. Основные свойства проекции.

Пусть в пространстве задана ось l (направленная прямая) и т. М, не лежащая на данной оси. Проекцией т. М на ось l называется основание М₁ перпендикуляра (нормали), опущенного из т. М на ось l. Если т. М лежит на оси, то проекция совпадет с точкой.

Дан вектор АВ^-, не равный 0, и ось l. Обозначу через А₁ и В₁ проекции точек на ось. Получился отрезок А₁В₁ меньшей длины, чем сам вектор. Проекцией АВ^- на ось l называется положительное число IА₁В₁I, если вектор и ось одинаково направленны; или же отрицательное число –IА₁В₁I, если они противоположны. А если т. А₁ и В₁ совпадают, то проекция равна 0.

Обозначается: пр._lАВ^- Можно записать символически: пр._lАВ^-=IА₁В₁I, если А₁В₁ (стрелки вверх, вверх) l или =- IА₁В₁I, если А₁В₁ (стрелки вниз, вверх) l.

Угол (у) между АВ^- и осью l получу сместив начало АВ^- на ось. Угол рассматривается обычно в промежутке от 0 до пи.

Свойства проекций.

1. Проекция а^- на ось l равна произведению Ia^-I на cos угла между вектором и осью: пр._lа^-=Ia^-I*cos<у

1 Следствие: Проекция >0, если вектор образует с осью острый угол; <0, если тупой угол; =0, если y=90.

2 Следствие: Проекции равных векторов на одну и ту же ось равны.

2. Проекция суммы n векторов на одну ось равна сумме их проекций на эту ось:

пр._l(a^-+b^-+c^-)=пр._lа^-+пр._lb^-+пр._lc^-

3. При умножении вектора на число его проекция на ось так же умножается на это число:

пр._l(h*a^-)=h*пр._la^-

16. Разложение вектора по ортам координатных осей. Координаты вектора.

Дана прямоугольная система координат Ох, Оу, Оz в трехмерном пространстве. Выделю единичные вектора (орты) на каждой оси и обозначу i, j, k. Начало произвольного вектора совмещу с началом координат. Обозначу проекции вектора на оси:

пр._Оха^-=а_х пр._Оуа^-=а_у пр._Оzа^-=а_z

Нужно указать, что: а^-=а_х*i+a_y*j+a_z*k Это разложение любого вектора по ортам координатных осей. Чсла а_х, а_у, а_z называются координатами вектора а^-, т. е. координаты вектора – его проекции на ось. Данное равенство также записывается: а^-=(а_х;a_y;a_z).

• Формула вычисления модуля вектора через его координаты. Направляющие косинусы.

Зная проекции вектора, можно найти его модуль (длину): Ia^-I=квадратный корень из а²_х+а²_у+а²_z

Модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.

Рассмотрев углы, образованные а^- с Ох, Оу, Оz, обозначу их как: <a, <B, <y. По 1 свойству проекций вектора на ось имеем: а_х=Ia^-I*cos<a a_y=Ia^-I*cos<B a_z=Ia^-I*cos<y Выражу косинусы:

cos<a= а_х/ Ia^-I cos<B= a_y/ Ia^-I cos<y= a_z/Ia^-I Эти числа и есть направляющие косинусы.

Нужно указать, что: cos²<a+ cos²<B + cos²<y =1

• Действия над векторами, заданными своими координатами: линейные операции, равенства.

Линейные операции.

Линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями векторов (свойства 2 и 3). Т. к.:

а^-=(а_х;a_y;a_z) или а^-=а_х*i+a_y*j+a_z*k

в^-=(в_х;в_y;в_z) или в^-=в_х*i+в_y*j+в_z*k

То нужно записать:

1. а^-+в^-=(а_х+в_х)*i+(a_y+в_у)*j+(a_z+в_z)*k

2. ha^-=h*а_х*i+h*a_y*j+h*a_z*k ha^-=(h*а_х;h*a_y;h*a_z)

При сложении векторов складываются одноименные координаты, при умножении вектора на число умножаются все его координаты на число.

Равенство векторов.

Из определения вектора, как наравленного отрезка, следует, что два вектора равнытогда и только тогда, когда равны соответствующие координаты этих векторов:

а^-=(а_х;a_y;a_z) в^-=(в_х;в_y;в_z) а^-= в^- если а_х= в_х, a_y=в_y, a_z=в_z

• Условие коллинеарности векторов.

Условие коллинеарности можно записать в виде: а^-=h*в^-, где h принадлежит R

а^- (палки вверх) в^- если а^-=h*в^-

Разложу по ортам координатных осей:

а_х*i+a_y*j+a_z*k= h*в_х*i+h*в_y*j+h*в_z*k Свяжу с условием одноименные координаты:

из а_х=h*в_х, а_у=h*в_у, а_z=h*в_z следует h=а_х/в_х, h=а_y/в_y, h=а_z/в_z

Значит, h=а_х/в_х=а_y/в_y=а_z/в_z Это и есть условие коллинеарности векторов в координатной форме. Таким образом 2-а вектора коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны.

• Скалярное произведение векторов. Свойства.

Скалярное произведение векторов.

Скалярное произведение 2-х ненулевых векторов – число, равное произведению длин этих векторов на косинус угла между ними. Результат – число.

а^-*в^-=Ia^-I*Iв^-I*cos<фи где фи – угол между векторами

Можно преобразовать: из Ia^-I*cos<фи=пр._в-а^- и Iв^-I*cos<фи=пр._а-в^- следует

а^-*в^-= пр._в-а^-* Iв^-I или а^-*в^-= пр._а-в^-*Ia^-I

Т. е. скалярное произведение 2-х векторов равно модудю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

Свойства.

1. Переместительное а^-*в^-=в^-* а^-

2. Сочетательное, относительно скалярного множителя

Если h принадлежит R, то (h*а^-)*в^-= h*(а^-*в^-)

3. Распределительное а^-*( в^-+с^-)= а^-*в^-+ а^-*с^-

4. Скалярный квадрат вектора равен квадрату его длины

а^2-= а^-*а^-= Ia^-I*Ia^-I*cos0= Ia^-I² В частности i²=j²=k²=1

Если а^- возвести скалярно в квадрат, а затем извлечь корень, то получится не первоначальное число, а число, равное модулю этого вектора: квадратный корень из а^2-= Ia^-I

5. Если а^- и в^- (не нулевые) взаимно перпендикулярны, то их скалярное произведение равно 0, т. к. cos<90=0.

Справедливои обратное утверждение: если скалярное произведение векторов, не равных 0, равно 0, то эти векторы взаимно перпендикулярны. В частности:

i*j=0 i*k=0 j*k=0 i*j=i*k=j*k=0

• Выражение скалярного произведения векторов через координаты. Угол между векторами. Условие ортогональности.

Выражение скалярного произведения через координаты.

Пусть заданы а^- и в^- через разложение по ортам координат осей

а^-=а_х*i+a_y*j+a_z*k в^-=в_х*i+в_y*j+в_z*k

Найду скалярное произведение векторов, перемножая их как многочлены (согласно свойствам 1,2,3 скалярного произведения). При умножении будем пользоваться таблицей скалярного произведения i, j, k (по свойствам 4 и 5):

	i	j	k
i	1	0	0
j	0	1	0
k	0	0	1

а^-*в^-= (а_х*i+a_y*j+a_z*k)*( в_х*i+в_y*j+в_z*k)=а_х*в_х+a_y*в_y+a_z*в_z

Скалярное произведение векторов равно сумме произведений их одноименых координат.

Угол между векторами.

а^-*в^-=Ia^-I*Iв^-I*cos<фи

cos<фи=(а^-*в^-)/(Ia^-I*Iв^-I)=( а_х*в_х+a_y*в_y+a_z*в_z)/(квадр. корень из а²_x+a²_y+a²_z)*(квадр. корень из в_х²+в_y²+в_z²)

Условие ортогональности.

Следствие: Если фи=90 (а^- в^-), то а^-*в^-=0 , т. е. а_х*в_х+a_y*в_y+a_z*в_z=0 Это условие перпендикулярности, или ортогональности, векторов в трехмерной системе координат.

• Векторное произведение. Свойства.

Векторное произведение

Векторным произведением двух векторов называется вектор, который

перпендикулярен плоскости перемножаемых векторов;

направлен туда, откуда видится поворот первого множителя вектора ко второму против часовой стрелки;

его модуль равен произведению модулей перемножаемых векторов на синус угла между ними:

Свойства :

Векторное произведение коллинеарных векторов равно нулю.

, где α и β числа,

,

.

• Выражение векторного произведения через координаты.

Векторное произведение в координатах

Представим перемножаемые векторы в разложении по базисным векторам декартовой системы координат и перемножим их, воспользовавшись свойствами векторного произведения,

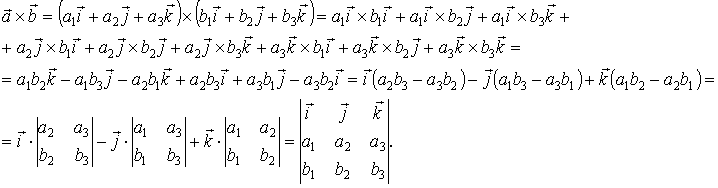
• Выражение векторного произведения через координаты

Условие комплонарности .Условие паралейности

- компланарны.

Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.

• Определение площади параллелограмма,припомощи векторного произведения

Формуле вычисления площади параллелограмма можно придать более простой вид через скалярное произведение:

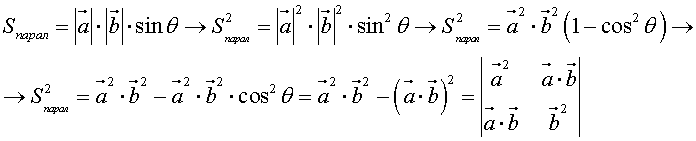
или окончательно

• Смешаное произведение вектора .Геометрический смысл произведение.

Рассмотрим произведение векторов а, b и с, составленное следующим образом: (ахb )•с. Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторноскалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.

Геометрический смысл выражения (ахb )*с. Построим параллелепипед, ребрами которого являются векторы а, b , с и вектор d =ахb

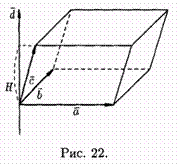
Имеем: (а х b) • с = d • с = |d| • прdс, |d|=|а х b| =S, где S — площадь параллелограмма, построенного на векторах а и b, прdс = Н Для правой тройки векторов и прdс = - Н для левой, где Н— высота параллелепипеда. Получаем: (axb )*c =S *(±H ), т. е. (axb )*c =±V , где V — объем параллелепипеда, образованного векторами а, b и с.

Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.

27.

Св-ва смешаного произведения

1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (а х b )•с=(b х с)•а=(с х а)•b .

Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер

2. Смешанное произведение не меняется при перемене местами знаков вкторного и скалярного умножения, т. е. (ахb )•с=а*(bx с).

Действительно, (ахb )•с=±V и а•(b хс)=(b хс)•а=±V . Знак в правой части этих равенств берем один и тот же, так как тройки векторов а , b , с и b , с , а — одной ориентации.

Следовательно, (a хb )•с=a (b хс). Это позволяет записывать смешанное произведение векторов (а х b )с в виде abc без знаков векторного, скалярного умножения.

3. Смешанное произведение меняет свой знак при перемене мест любых вух векторов-сомножителей, т. е. abc =-acb , abc =-bac , abc =-cba .

Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.

4.Смешанное произведение ненулевых векторов а, b и с равно нулю огда и только тогда, когда они компланарны.

Если abc =0 , то а, b и с— компланарны.

Допустим, что это не так. Можно было бы построить параллелепипед с объемом V¹ 0. Но так как abc =±V , то получили бы, что abc¹0 . Это противоречит условию: abc =0.

Обратно, пусть векторы а, b , с — компланарны. Тогда вектор d =ахb будет перпендикулярен плоскости, в которой лежат векторы а, b ,с, и следовательно, d ^с. Поэтому d •с=0, т. е. abc =0.

28.

Выражение смешанного произведения через координаты

Пусть заданы векторы a =ахi +ayj +azk , b =bxi +byj +bzk , с=cxi +cyj +czk . Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:

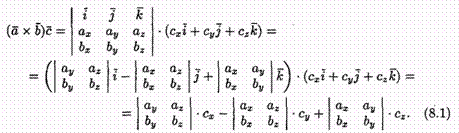
Полученную формулу можно записать короче:

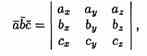
так как правая часть равенства (8.1) представляет собой разложение определителя третьего порядка по элементам третьей строки.

Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.

29)

Общее уравнение прямой

Общее уравнение прямой линии на плоскости в декартовых координатах:

где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.

При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде :

Всякое уравнение первой степени относительно х и у, т.е. уравнение вида Ax+By+C=0

(где А, В и С- постоянные коэффициенты, причем А2+В2≠0) определяет на плоскости некоторую прямую. Это уравнение называется общим уравнением прямой.

Частные случаи:

1. С=0; А≠0; В≠0. Прямая, определяемая уравнением Ах+Ву=0, проходит через начало координат.

2. А=0, В≠0; С≠0. Прямая, определяемая уравнением Ву+С=0 (или у=b, где ), параллельна оси (ох).

3. В=0; А≠0; С≠0. Прямая, определяемая уравнением Ах+С=0 , параллельна оси Оу.

4. В=С=0; А≠0. Прямая определяемая уравнением Ах=0 (или x=0 поскольку А≠0), совпадает с осью Оу.

5. А=С=0; В≠0. Прямая, определяемая уравнением Ву=0 (или у=0, поскольку В≠0), совпадает с осью Oх.

Если в общем уравнении прямой В≠0, то, разрешив его относительно у, получим уравнение вида y=kx+в . Его называют уравнением с угловым коэффициентом поскольку где -угол, образованный прямой с положительным направлением оси Oх. Свободный член уравнения в равен ординате точки пересечения прямой с осью Oу.

30.

Пусть прямые l1 и l2 заданы общими уравнениями

A1x + В1у + C1 = 0 и А2х + В2 y + С2 = 0.

Согласно формуле:

и, следовательно, косинус угла φ между прямыми l1 и l2 может быть вычислен по формуле:

Записав правую часть формулы через координаты, получим:

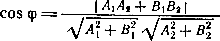
Прямые с нормальными векторами n1 и n2: (Условия параллельности и перпендикулярности двух прямых)

а) параллельны тогда и только тогда, когда векторы n1 и n2 коллинеарны;

б) перпендикулярны тогда и только тогда, когда векторы n1 и n2 перпендикулярны, т. е. когда n1 • n2 = 0.

Отсюда получаем необходимые и достаточные уcловия параллельности и перпендикулярности двух прямых, заданных общими уравнениями.

Для того чтобы прямые

A1x + В1у + C1 = 0 и А2х + В2 y + С2 = 0

были:

а) параллельны, необходимо и достаточно, чтобы

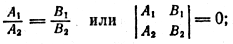
б) перпендикулярны, необходимо и достаточно, чтобы

A1A2 + В1В2 = 0

31.

Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой, проходящей через эти точки:

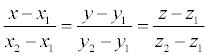
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.

На плоскости записанное выше уравнение прямой упрощается:

если х 1 ≠ х2 и х = х 1 , если х 1 = х2 .

Дробь = k называется угловым коэффициентом прямой.

Уравнение прямой по точке и направляющему вектору

По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой.

Определение. Каждый ненулевой вектор ( α1 , α2 ), компоненты которого удовлетворяют условию А α1 + В α2 = 0 называется направляющим вектором прямой

Ах + Ву + С = 0.

Пример. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:

1 * A + (-1) * B = 0, т.е. А = В.

Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.

при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:

х + у - 3 = 0